概率预测

在这个例子中，我们将实现预测区间

本教程假设您对 MLForecast 有基本的了解。如需查看最简单的示例，请访问 快速入门

介绍

当我们生成预测时，通常会产生一个称为点预测的单一值。然而，这个值并不能告诉我们与预测相关的不确定性。为了衡量这种不确定性，我们需要预测区间。

预测区间是预测可能取值的一个范围，该范围具有给定的概率。因此，一个95%的预测区间应包含一个值的范围，以95%的概率包含实际的未来值。概率预测旨在生成完整的预测分布。另一方面，点预测通常返回该分布的均值或中位数。然而，在现实场景中，预测不仅最可能的未来结果，而且许多替代的结果通常更好。

使用MLForecast，您可以训练sklearn模型来生成点预测。它还利用ConformalPrediction的优势来生成相同的点预测，并为它们添加预测区间。在本教程的最后，您将对如何为时间序列预测的sklearn模型添加概率区间有一个很好的理解。此外，您还将学习如何生成包含历史数据、点预测和预测区间的图表。

重要

尽管这些术语经常混淆，但预测区间与置信区间并不相同。

警告

在实践中，大多数预测区间都过于狭窄，因为模型未考虑所有不确定性来源。关于这一点的讨论可以在这里找到。

大纲：

  1. 安装库
  2. 加载和探索数据
  3. 训练模型
  4. 绘制预测区间
Tip

您可以使用 Colab 交互式运行此笔记本 在 Colab 中打开

安装库

使用 pip install mlforecast utilsforecast 安装必要的包。

加载和探索数据

在这个例子中，我们将使用来自M4 Competition的小时数据集。我们首先需要从一个网址下载数据，然后将其加载为一个 pandas 数据框。请注意，我们将分别加载训练数据和测试数据。我们还将把测试数据的 y 列重命名为 y_test。

import pandas as pd
from utilsforecast.plotting import plot_series
train = pd.read_csv('https://auto-arima-results.s3.amazonaws.com/M4-Hourly.csv')
test = pd.read_csv('https://auto-arima-results.s3.amazonaws.com/M4-Hourly-test.csv')
train.head()
unique_id ds y
0 H1 1 605.0
1 H1 2 586.0
2 H1 3 586.0
3 H1 4 559.0
4 H1 5 511.0 
test.head()
unique_id ds y
0 H1 701 619.0
1 H1 702 565.0
2 H1 703 532.0
3 H1 704 495.0
4 H1 705 481.0

由于本笔记本的目标是生成预测区间，因此我们将仅使用数据集的前8个系列，以减少总计算时间。

n_series = 8 
uids = train['unique_id'].unique()[:n_series] # 选择数据集中的前n_series个序列
train = train.query('unique_id in @uids')
test = test.query('unique_id in @uids')

我们可以使用utilsforecast库中的plot_series函数来绘制这些系列。该函数有多个参数，生成本笔记本中图表所需的参数解释如下。

  • df：一个包含[unique_id, ds, y]列的pandas数据框。
  • forecasts_df：一个包含[unique_id, ds]和模型的pandas数据框。
  • plot_random：bool = True。随机绘制时间序列。
  • models：List[str]。我们想要绘制的模型列表。
  • level：List[float]。我们想要绘制的预测区间列表。
  • engine：str = matplotlib。也可以是plotly。plotly生成交互式图表，而matplotlib生成静态图表。
fig = plot_series(train, test.rename(columns={'y': 'y_test'}), models=['y_test'], plot_random=False)

fig.savefig('../../figs/prediction_intervals__eda.png', bbox_inches='tight')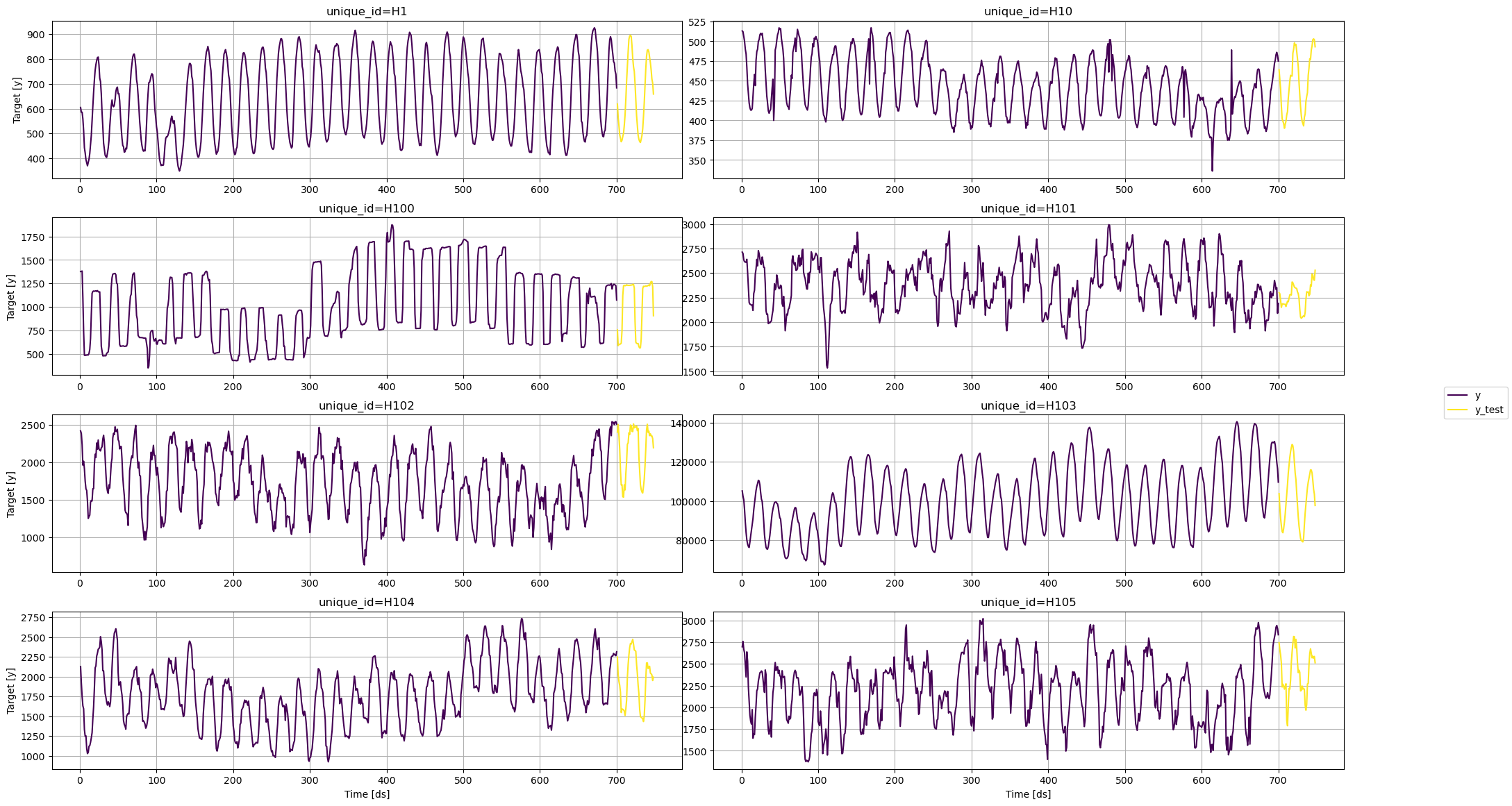

训练模型

MLForecast可以高效地在不同时间序列上训练遵循sklearn语法（fit和predict）的多个模型。

在这个例子中，我们将使用以下sklearn基础模型：

要使用这些模型，我们首先需要从sklearn导入它们，然后需要实例化它们。

from mlforecast import MLForecast
from mlforecast.target_transforms import Differences
from mlforecast.utils import PredictionIntervals
from sklearn.linear_model import Lasso, LinearRegression, Ridge
from sklearn.neighbors import KNeighborsRegressor
from sklearn.neural_network import MLPRegressor
# 创建一个模型及其实例化参数的列表 
models = [
    KNeighborsRegressor(),
    Lasso(),
    LinearRegression(),
    MLPRegressor(),
    Ridge(),
]

要实例化一个新的 MLForecast 对象，我们需要以下参数：

  • models: 在前一步中定义的模型列表。
  • target_transforms: 在计算特征之前应用于目标的变换。这些在预测步骤中恢复。
  • lags: 用作特征的目标滞后值。
mlf = MLForecast(
    models=[Ridge(), Lasso(), LinearRegression(), KNeighborsRegressor(), MLPRegressor(random_state=0)],
    freq=1,
    target_transforms=[Differences([1])],
    lags=[24 * (i+1) for i in range(7)],
)

现在我们准备生成点预测和预测区间。为此，我们将使用 fit 方法，该方法接受以下参数：

  • data：长格式的系列数据。
  • id_col：识别每个系列的列。在我们的例子中是 unique_id。
  • time_col：识别每个时间步的列，其值可以是时间戳或整数。在我们的例子中是 ds。
  • target_col：包含目标的列。在我们的例子中是 y。
  • prediction_intervals：一个 PredictionIntervals 类。该类接受两个参数：n_windows 和 h。n_windows 代表用于校准区间的交叉验证窗口的数量，而 h 是预测范围。该策略会根据每个范围步调整区间，因此每个步的宽度会有所不同。
mlf.fit(
    train,
    prediction_intervals=PredictionIntervals(n_windows=10, h=48),
);

在拟合模型后，我们将调用 predict 方法生成带有预测区间的预测。该方法接受以下参数：

  • horizon：表示预测时间范围的整数。在这种情况下，我们将预测接下来的48小时。
  • level：一个包含预测区间置信水平的浮点数列表。例如，level=[95] 意味着该值范围应该以95%的概率包含实际未来值。
levels = [50, 80, 95]
forecasts = mlf.predict(48, level=levels)
forecasts.head()
unique_id ds Ridge Lasso LinearRegression KNeighborsRegressor MLPRegressor Ridge-lo-95 Ridge-lo-80 Ridge-lo-50 ... KNeighborsRegressor-lo-50 KNeighborsRegressor-hi-50 KNeighborsRegressor-hi-80 KNeighborsRegressor-hi-95 MLPRegressor-lo-95 MLPRegressor-lo-80 MLPRegressor-lo-50 MLPRegressor-hi-50 MLPRegressor-hi-80 MLPRegressor-hi-95
0 H1 701 612.418170 612.418079 612.418170 615.2 612.651532 590.473256 594.326570 603.409944 ... 609.45 620.95 627.20 631.310 584.736193 591.084898 597.462107 627.840957 634.218166 640.566870
1 H1 702 552.309298 552.308073 552.309298 551.6 548.791801 498.721501 518.433843 532.710850 ... 535.85 567.35 569.16 597.525 497.308756 500.417799 515.452396 582.131207 597.165804 600.274847
2 H1 703 494.943384 494.943367 494.943384 509.6 490.226796 448.253304 463.266064 475.006125 ... 492.70 526.50 530.92 544.180 424.587658 436.042788 448.682502 531.771091 544.410804 555.865935
3 H1 704 462.815779 462.815363 462.815779 474.6 459.619069 409.975219 422.243593 436.128272 ... 451.80 497.40 510.26 525.500 379.291083 392.580306 413.353178 505.884959 526.657832 539.947054
4 H1 705 440.141034 440.140586 440.141034 451.6 438.091712 377.999588 392.523016 413.474795 ... 427.40 475.80 488.96 503.945 348.618034 362.503767 386.303325 489.880099 513.679657 527.565389

5 rows × 37 columns

test = test.merge(forecasts, how='left', on=['unique_id', 'ds'])

绘制预测区间

为了绘制点和预测区间，我们将再次使用 plot_series 函数。请注意，现在我们还需要指定要绘制的模型和水平。

KNeighborsRegressor

fig = plot_series(
    train, 
    test, 
    plot_random=False, 
    models=['KNeighborsRegressor'], 
    level=levels, 
    max_insample_length=48
)

fig.savefig('../../figs/prediction_intervals__knn.png', bbox_inches='tight')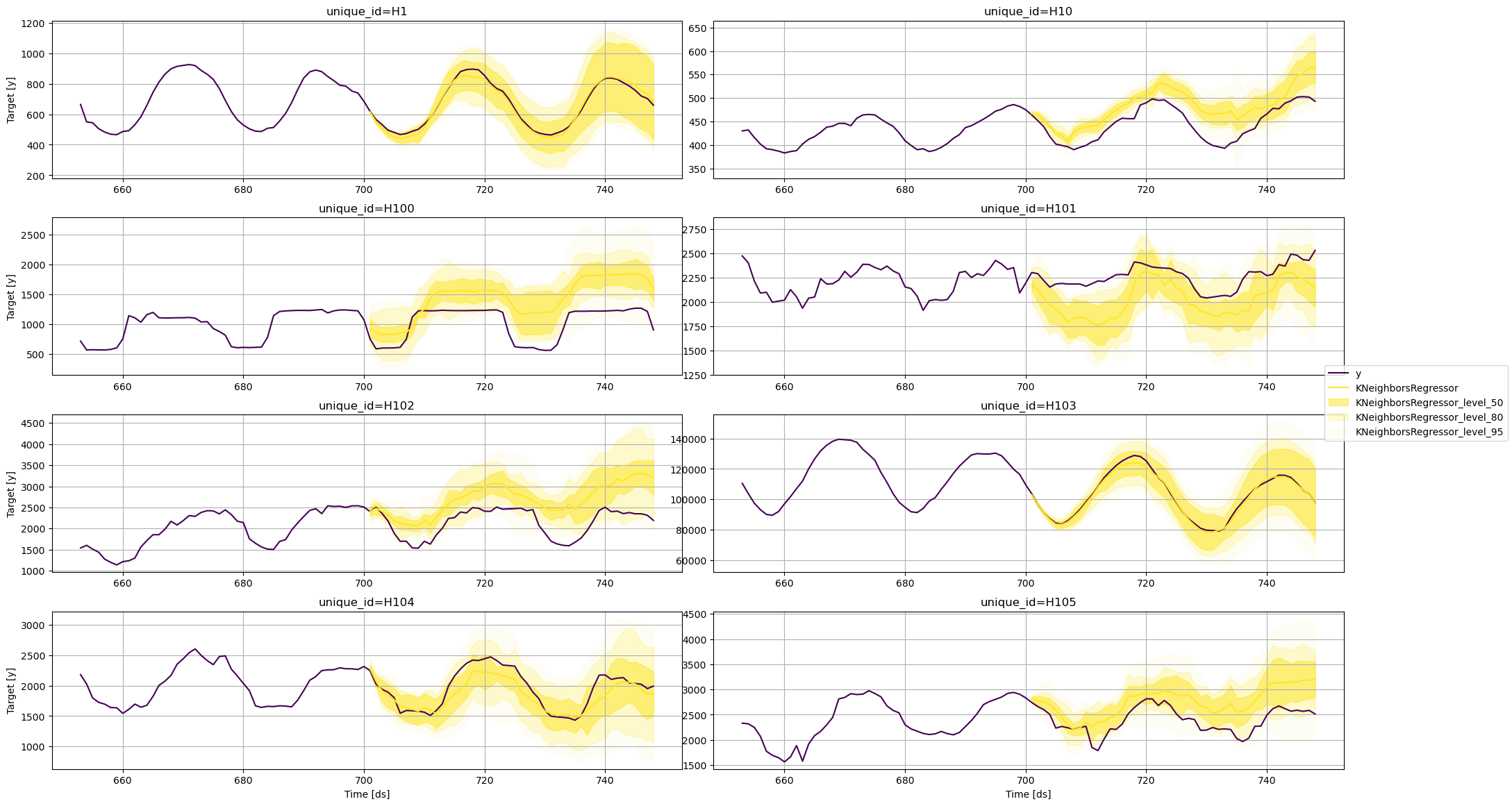

套索回归

fig = plot_series(
    train, 
    test, 
    plot_random=False, 
    models=['Lasso'],
    level=levels, 
    max_insample_length=48
)

fig.savefig('../../figs/prediction_intervals__lasso.png', bbox_inches='tight')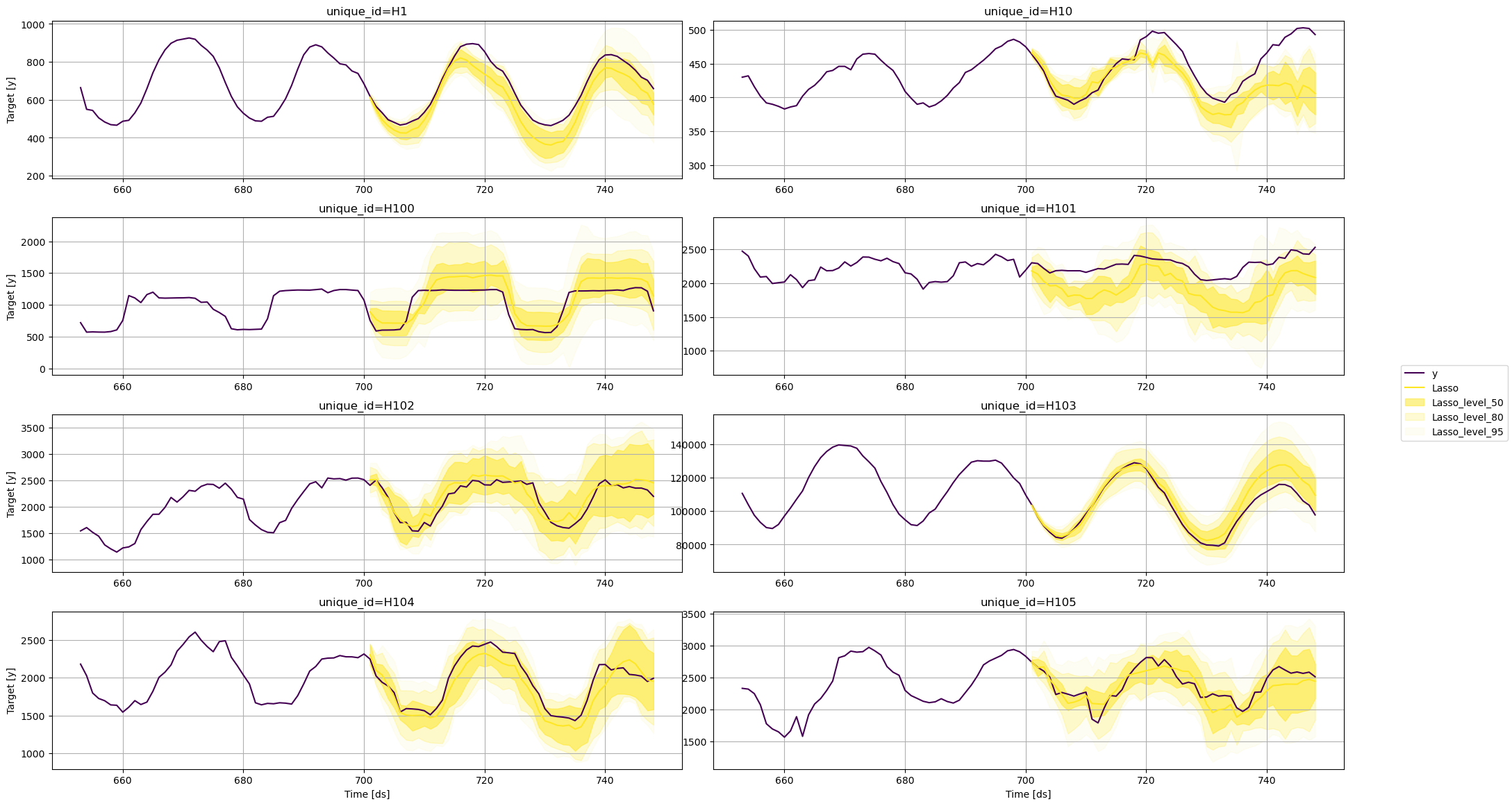

线性回归

fig = plot_series(
    train, 
    test, 
    plot_random=False, 
    models=['LinearRegression'],
    level=levels, 
    max_insample_length=48
)

fig.savefig('../../figs/prediction_intervals__lr.png', bbox_inches='tight')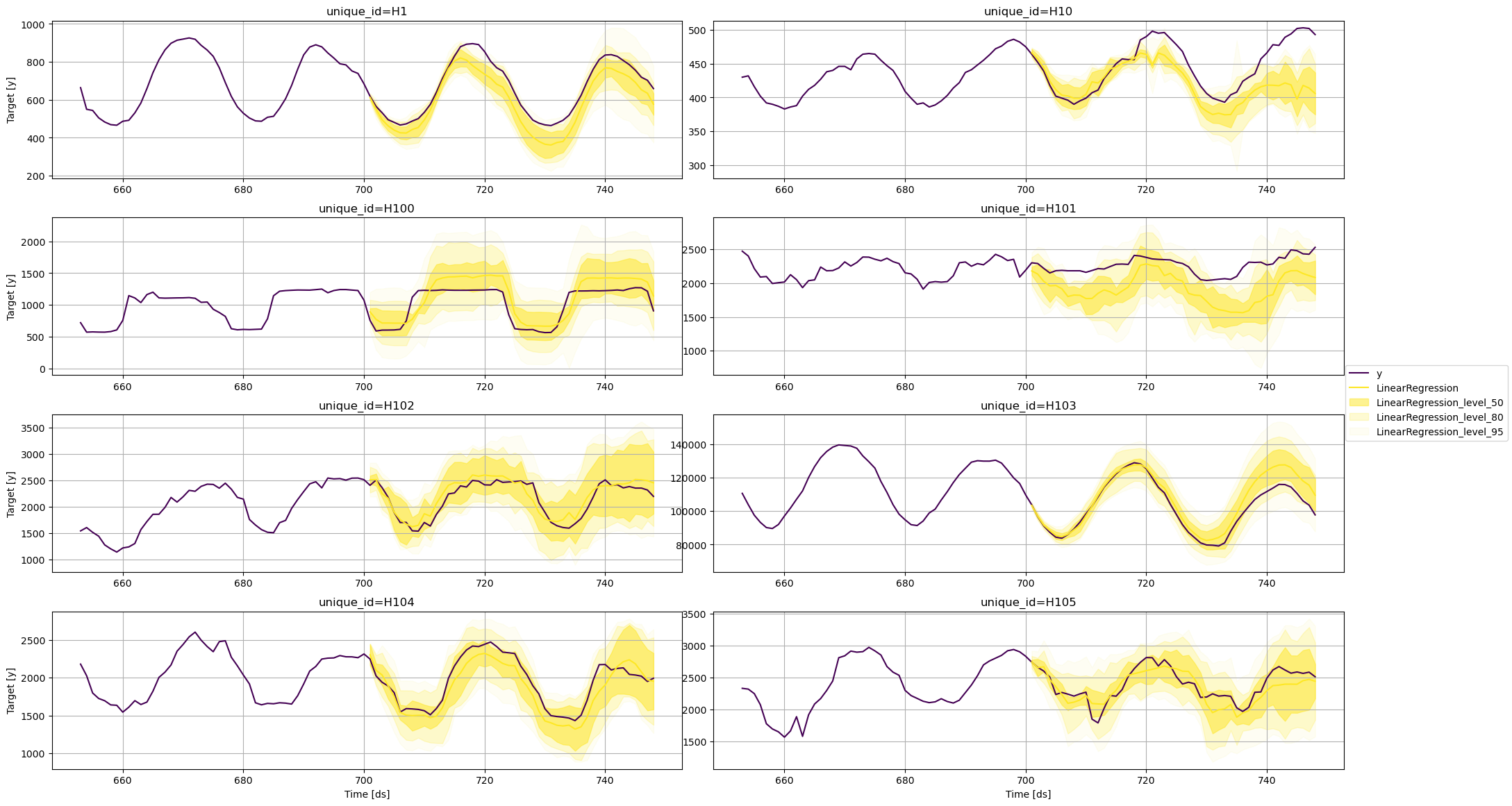

MLP回归器

fig = plot_series(
    train, 
    test, 
    plot_random=False, 
    models=['MLPRegressor'],
    level=levels, 
    max_insample_length=48
)

fig.savefig('../../figs/prediction_intervals__mlp.png', bbox_inches='tight')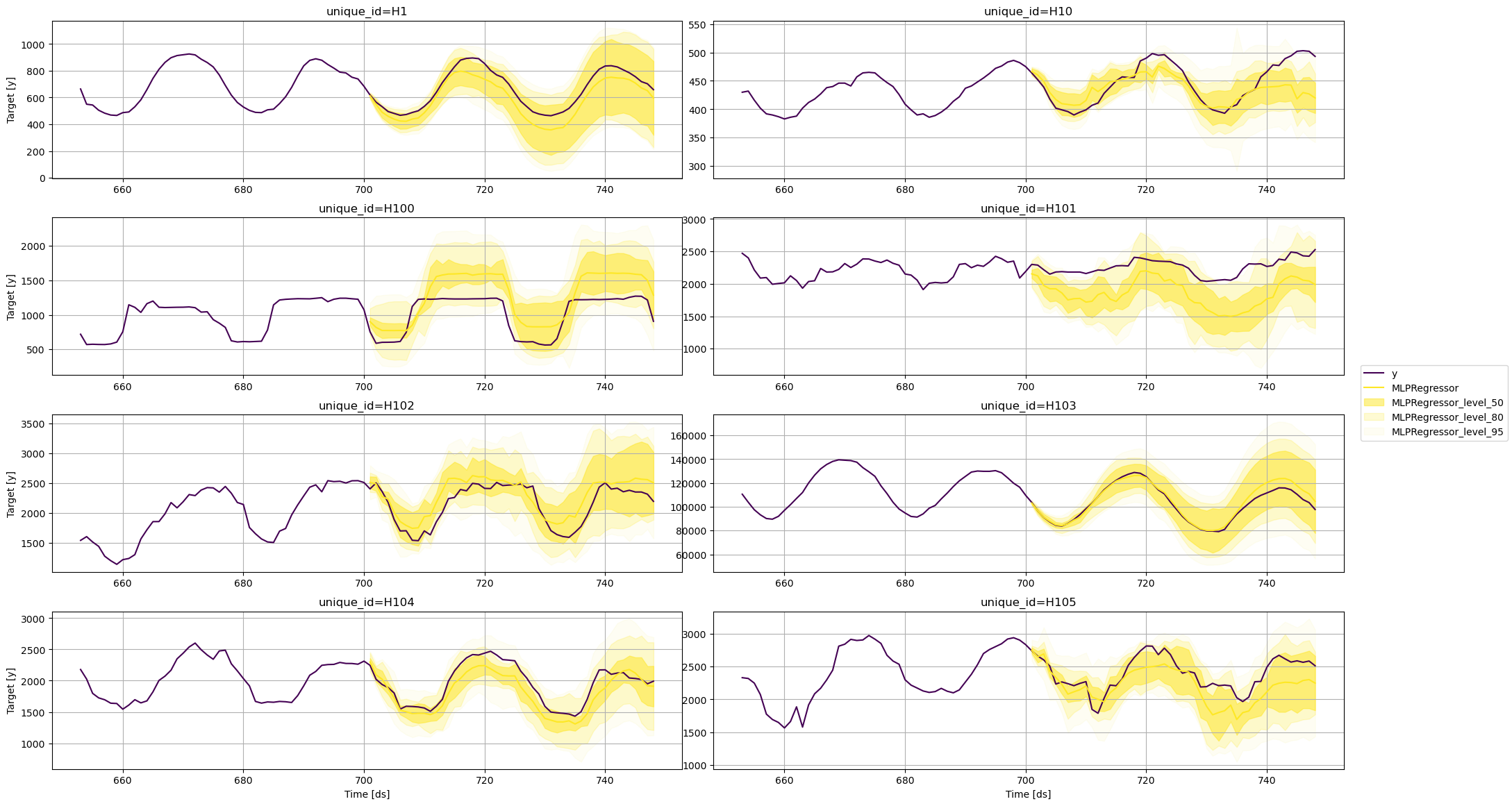

岭回归

fig = plot_series(
    train, 
    test, 
    plot_random=False, 
    models=['Ridge'],
    level=levels, 
    max_insample_length=48
)

fig.savefig('../../figs/prediction_intervals__ridge.png', bbox_inches='tight')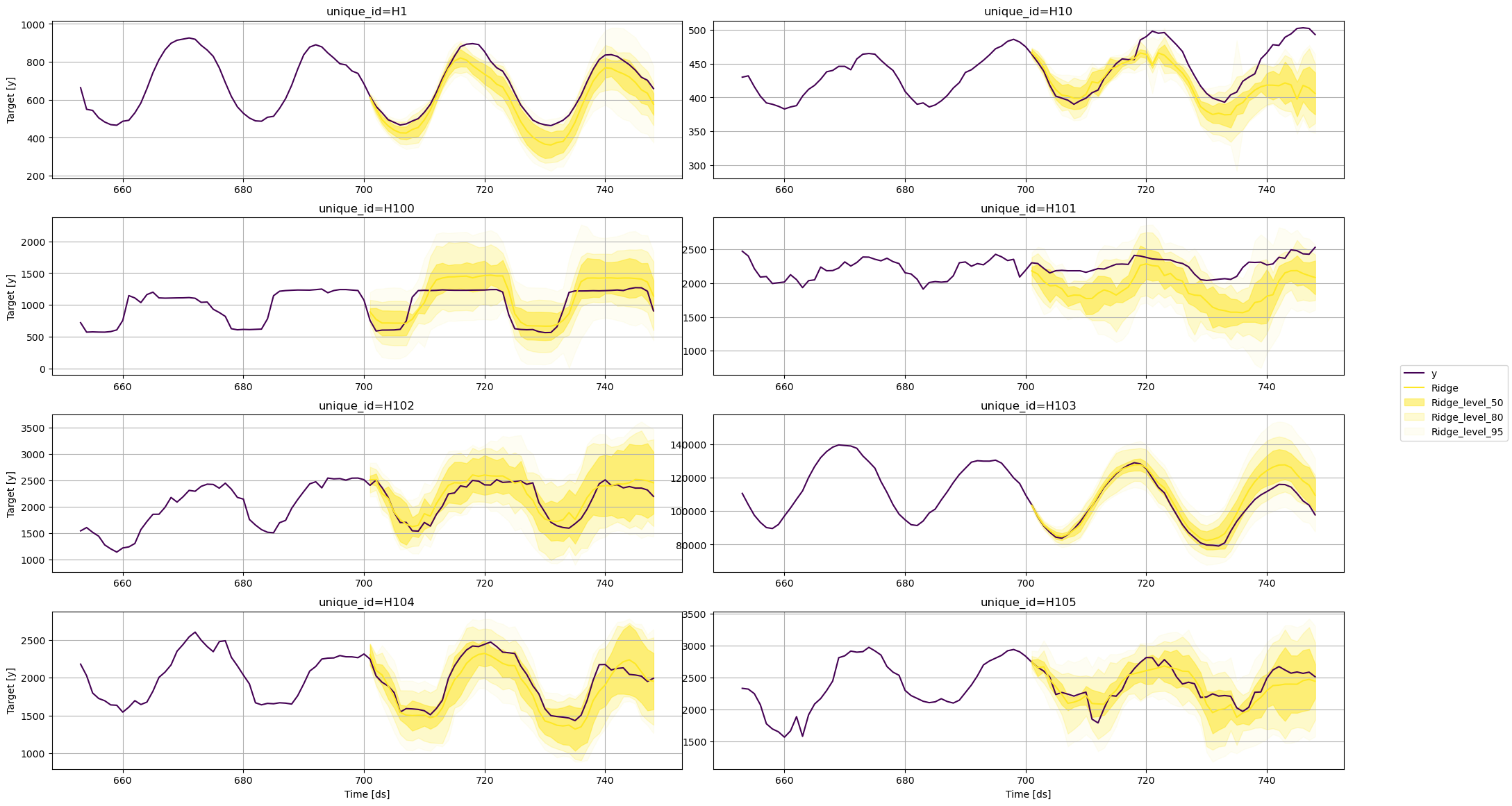

从这些图中，我们可以得出结论，各个预测的不确定性因所使用的模型而异。对于相同的时间序列，一个模型可能预测出比其他模型更广泛的未来可能值范围。

参考文献

Give us a ⭐ on Github