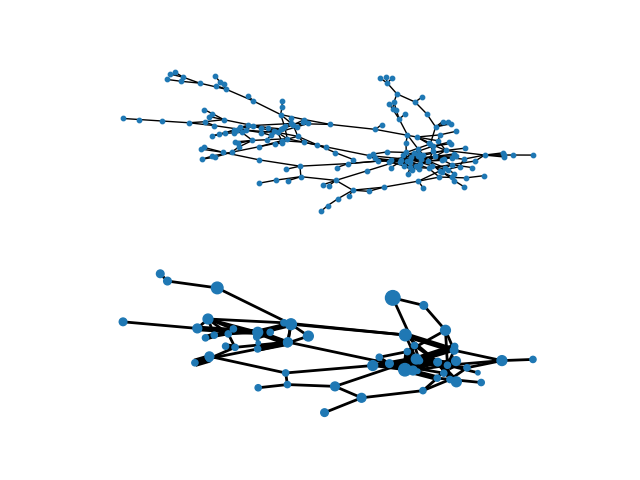
块模型

使用NX中的quotient_graph函数创建块模型的示例。所用数据为哈特福德市（康涅狄格州）吸毒者网络:

@article{weeks2002social,
  title={高风险地点吸毒者的社交网络：寻找联系},
  url = {https://doi.org/10.1023/A:1015457400897},
  doi = {10.1023/A:1015457400897},
  author={Weeks, Margaret R and Clair, Scott and Borgatti, Stephen P and Radda, Kim and Schensul, Jean J},
  journal={{艾滋病与行为}},
  volume={6},
  number={2},
  pages={193--206},
  year={2002},
  publisher={Springer}
}

from collections import defaultdict

import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
from scipy.cluster import hierarchy
from scipy.spatial import distance


def create_hc(G):
    """从距离矩阵创建图G的层次聚类"""
    path_length = nx.all_pairs_shortest_path_length(G)
    distances = np.zeros((len(G), len(G)))
    for u, p in path_length:
        for v, d in p.items():
            distances[u][v] = d
    # 创建层次聚类
    Y = distance.squareform(distances)
    Z = hierarchy.complete(Y)  # 使用最远点链接创建层次聚类
    # 这个分区选择是任意的，仅用于说明目的
    membership = list(hierarchy.fcluster(Z, t=1.15))
    # 创建用于块模型的列表集合
    partition = defaultdict(list)
    for n, p in zip(list(range(len(G))), membership):
        partition[p].append(n)
    return list(partition.values())


G = nx.read_edgelist("hartford_drug.edgelist")

# 提取最大的连通分量到图H中
H = G.subgraph(next(nx.connected_components(G)))
# 使生活更轻松，拥有连续标记的整数节点
H = nx.convert_node_labels_to_integers(H)
# 使用层次聚类创建分区
partitions = create_hc(H)
# Build blockmodel graph
BM = nx.quotient_graph(H, partitions, relabel=True)

# Draw original graph
pos = nx.spring_layout(H, iterations=100, seed=83)  # 用于可重复性的种子
plt.subplot(211)
nx.draw(H, pos, with_labels=False, node_size=10)

# 绘制带权重的边和节点大小的块模型，节点大小由内部节点数量决定
node_size = [BM.nodes[x]["nnodes"] * 10 for x in BM.nodes()]
edge_width = [(2 * d["weight"]) for (u, v, d) in BM.edges(data=True)]
# 将位置设置为原始图中内部节点位置的平均值
posBM = {}
for n in BM:
    xy = np.array([pos[u] for u in BM.nodes[n]["graph"]])
    posBM[n] = xy.mean(axis=0)
plt.subplot(212)
nx.draw(BM, posBM, node_size=node_size, width=edge_width, with_labels=False)
plt.axis("off")
plt.show()