scipy.interpolate.

BarycentricInterpolator

class scipy.interpolate.BarycentricInterpolator(xi, yi=None, axis=0, *, wi=None, random_state=None)

一组点的插值多项式。

构建一个通过给定点的多项式。允许对多项式及其所有导数进行求值，高效地改变要插值的y值，并通过添加更多的x和y值进行更新。

出于数值稳定性的考虑，此函数不计算多项式的系数。

在函数求值之前，需要提供 yi 的值，但没有任何预处理依赖于它们，因此可以快速更新。

参数:

xiarray_like, 形状 (npoints, )

多项式应通过的点的x坐标的一维数组

一类似数组，形状 (…, npoints, …), 可选

多项式应通过的点的y坐标的N-D数组。如果为None，y值将通过`set_y`方法稍后提供。沿插值轴的`yi`长度必须等于`xi`的长度。使用``axis``参数选择正确的轴。

轴int, 可选

yi 数组中对应于 x 坐标值的轴。默认为 axis=0。

wi类似数组, 可选

所选插值点 xi 的重心权重。如果缺失或为 None，将从 xi 计算权重（默认）。这允许在多个插值计算使用相同的节点 xi 时，重复使用权重 wi，而无需重新计算。

random_state : {None, int, numpy.random.Generator, numpy.random.RandomState}, 可选{None, int,}

如果 seed 是 None（或 np.random），则使用 numpy.random.RandomState 单例。如果 seed 是 int，则使用新的 RandomState 实例，并以 seed 为种子。如果 seed 已经是 Generator 或 RandomState 实例，则使用该实例。

属性:

dtype

方法

__call__(x)	在点 x 处评估插值多项式
add_xi(xi[, yi])	向要插值的集合中添加更多 x 值
derivative(x[, der])	在点 x 处评估多项式的单个导数。
derivatives(x[, der])	在点 x 处评估多项式的几个导数
set_yi(yi[, axis])	更新 y 值以进行插值

注释

此类使用一种“重心插值”方法，将问题视为有理函数插值的特殊情况。该算法在数值上相当稳定，但在精确计算的世界中，除非 x 坐标选择得非常仔细——例如，Chebyshev 零点（如 cos(i*pi/n)）是一个不错的选择——否则由于 Runge 现象，多项式插值本身是一个非常病态的过程。

基于 Berrut 和 Trefethen 2004 年的论文，《重心拉格朗日插值》。

示例

Try it in your browser!

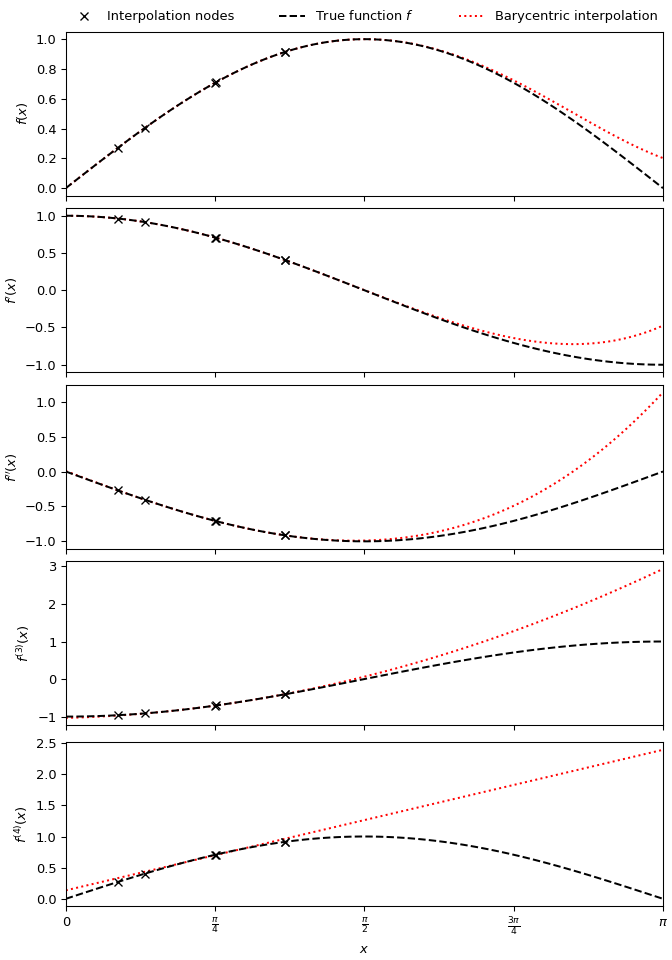
生成一个五次重心插值，近似函数 \(\sin x\) 及其前四阶导数，使用在 \((0, \frac{\pi}{2})\) 区间内随机分布的六个节点：

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import BarycentricInterpolator
>>> rng = np.random.default_rng()
>>> xi = rng.random(6) * np.pi/2
>>> f, f_d1, f_d2, f_d3, f_d4 = np.sin, np.cos, lambda x: -np.sin(x), lambda x: -np.cos(x), np.sin
>>> P = BarycentricInterpolator(xi, f(xi), random_state=rng)
>>> fig, axs = plt.subplots(5, 1, sharex=True, layout='constrained', figsize=(7,10))
>>> x = np.linspace(0, np.pi, 100)
>>> axs[0].plot(x, P(x), 'r:', x, f(x), 'k--', xi, f(xi), 'xk')
>>> axs[1].plot(x, P.derivative(x), 'r:', x, f_d1(x), 'k--', xi, f_d1(xi), 'xk')
>>> axs[2].plot(x, P.derivative(x, 2), 'r:', x, f_d2(x), 'k--', xi, f_d2(xi), 'xk')
>>> axs[3].plot(x, P.derivative(x, 3), 'r:', x, f_d3(x), 'k--', xi, f_d3(xi), 'xk')
>>> axs[4].plot(x, P.derivative(x, 4), 'r:', x, f_d4(x), 'k--', xi, f_d4(xi), 'xk')
>>> axs[0].set_xlim(0, np.pi)
>>> axs[4].set_xlabel(r"$x$")
>>> axs[4].set_xticks([i * np.pi / 4 for i in range(5)],
...                   ["0", r"$\frac{\pi}{4}$", r"$\frac{\pi}{2}$", r"$\frac{3\pi}{4}$", r"$\pi$"])
>>> axs[0].set_ylabel("$f(x)$")
>>> axs[1].set_ylabel("$f'(x)$")
>>> axs[2].set_ylabel("$f''(x)$")
>>> axs[3].set_ylabel("$f^{(3)}(x)$")
>>> axs[4].set_ylabel("$f^{(4)}(x)$")
>>> labels = ['Interpolation nodes', 'True function $f$', 'Barycentric interpolation']
>>> axs[0].legend(axs[0].get_lines()[::-1], labels, bbox_to_anchor=(0., 1.02, 1., .102),
...               loc='lower left', ncols=3, mode="expand", borderaxespad=0., frameon=False)
>>> plt.show()

Go BackOpen In Tab