scipy.optimize.

根#

scipy.optimize.root(fun, x0, args=(), method='hybr', jac=None, tol=None, callback=None, options=None)[源代码][源代码]#

找到一个向量函数的根。

参数:

有趣可调用

一个用于寻找根的向量函数。

x0ndarray

初始猜测。

参数tuple, 可选

传递给目标函数及其雅可比矩阵的额外参数。

方法str, 可选

求解器类型。应为以下之一

‘hybr’ (见此处)

‘lm’ (见此处)

‘broyden1’ (见此处)

‘broyden2’ (见这里)

‘anderson’ (见此处)

‘linearmixing’ (见此处)

‘diagbroyden’ (见此处)

‘excitingmixing’ (见此处)

‘krylov’ (见这里)

‘df-sane’ (见此处)

jac布尔值或可调用对象，可选

如果 jac 是一个布尔值并且为 True，则假定 fun 返回目标函数以及雅可比矩阵的值。如果为 False，雅可比矩阵将通过数值方法估计。jac 也可以是一个返回 fun 雅可比矩阵的可调用对象。在这种情况下，它必须接受与 fun 相同的参数。

tolfloat, 可选

终止容差。如需详细控制，请使用特定求解器选项。

回调函数, 可选

可选的回调函数。它在每次迭代时被调用，形式为 callback(x, f)，其中 x 是当前的解，f 是对应的残差。对于除 ‘hybr’ 和 ‘lm’ 之外的所有方法。

选项dict, 可选

A dictionary of solver options. E.g., xtol or maxiter, see show_options() for details.

返回:

sol优化结果: 解决方案表示为一个 OptimizeResult 对象。重要属性包括：x 解决方案数组，success 一个布尔标志，指示算法是否成功退出，以及 message 描述终止原因。有关其他属性的描述，请参见 OptimizeResult。

参见

show_options: 求解器接受的附加选项

注释

本节描述了可以通过 ‘method’ 参数选择的可用求解器。默认方法是 hybr。

方法 hybr 使用了一种修改后的 Powell 混合方法，该方法在 MINPACK [1] 中实现。

方法 lm 使用 Levenberg-Marquardt 算法的修改版本来解决非线性方程组的最小二乘问题，该算法在 MINPACK [1] 中实现。

方法 df-sane 是一种无导数的谱方法。 [3]

方法 broyden1、broyden2、anderson、linearmixing、diagbroyden、excitingmixing、krylov 是非精确牛顿法，具有回溯或全行搜索 [2]。每种方法对应于特定的雅可比矩阵近似。

方法 broyden1 使用 Broyden 的第一种雅可比近似，它被称为 Broyden 的好方法。
方法 broyden2 使用 Broyden 的第二个雅可比近似，它被称为 Broyden 的坏方法。
方法 anderson 使用（扩展）Anderson混合。
方法 Krylov 使用 Krylov 近似逆雅可比矩阵。它适用于大规模问题。
方法 diagbroyden 使用对角 Broyden 雅可比近似。
方法 linearmixing 使用标量雅可比近似。
方法 excitingmixing 使用了一个调优的对角雅可比近似。

警告

为方法 diagbroyden、linearmixing 和 excitingmixing 实现的算法可能对特定问题有用，但它们是否有效可能强烈依赖于问题本身。

Added in version 0.11.0.

参考文献

[1] (1,2)

More, Jorge J., Burton S. Garbow, 和 Kenneth E. Hillstrom. 1980. MINPACK-1 用户指南。

[2]

C. T. Kelley. 1995. Iterative Methods for Linear and Nonlinear Equations. Society for Industrial and Applied Mathematics. <https://archive.siam.org/books/kelley/fr16/>

[3]

La Cruz, J.M. Martinez, M. Raydan. Math. Comp. 75, 1429 (2006).

示例

以下函数定义了一个非线性方程组及其雅可比矩阵。

>>> import numpy as np
>>> def fun(x):
...     return [x[0]  + 0.5 * (x[0] - x[1])**3 - 1.0,
...             0.5 * (x[1] - x[0])**3 + x[1]]

>>> def jac(x):
...     return np.array([[1 + 1.5 * (x[0] - x[1])**2,
...                       -1.5 * (x[0] - x[1])**2],
...                      [-1.5 * (x[1] - x[0])**2,
...                       1 + 1.5 * (x[1] - x[0])**2]])

解决方案可以如下获得。

>>> from scipy import optimize
>>> sol = optimize.root(fun, [0, 0], jac=jac, method='hybr')
>>> sol.x
array([ 0.8411639,  0.1588361])

大问题

假设我们需要在正方形 \([0,1]\times[0,1]\) 上求解以下积分微分方程：

\[\nabla^2 P = 10 \left(\int_0^1\int_0^1\cosh(P)\,dx\,dy\right)^2\]

在正方形边界上，满足 \(P(x,1) = 1\) 且 \(P=0\) 在其他地方。

可以使用 method='krylov' 求解器找到解决方案：

>>> from scipy import optimize
>>> # parameters
>>> nx, ny = 75, 75
>>> hx, hy = 1./(nx-1), 1./(ny-1)

>>> P_left, P_right = 0, 0
>>> P_top, P_bottom = 1, 0

>>> def residual(P):
...    d2x = np.zeros_like(P)
...    d2y = np.zeros_like(P)
...
...    d2x[1:-1] = (P[2:]   - 2*P[1:-1] + P[:-2]) / hx/hx
...    d2x[0]    = (P[1]    - 2*P[0]    + P_left)/hx/hx
...    d2x[-1]   = (P_right - 2*P[-1]   + P[-2])/hx/hx
...
...    d2y[:,1:-1] = (P[:,2:] - 2*P[:,1:-1] + P[:,:-2])/hy/hy
...    d2y[:,0]    = (P[:,1]  - 2*P[:,0]    + P_bottom)/hy/hy
...    d2y[:,-1]   = (P_top   - 2*P[:,-1]   + P[:,-2])/hy/hy
...
...    return d2x + d2y - 10*np.cosh(P).mean()**2

>>> guess = np.zeros((nx, ny), float)
>>> sol = optimize.root(residual, guess, method='krylov')
>>> print('Residual: %g' % abs(residual(sol.x)).max())
Residual: 5.7972e-06  # may vary

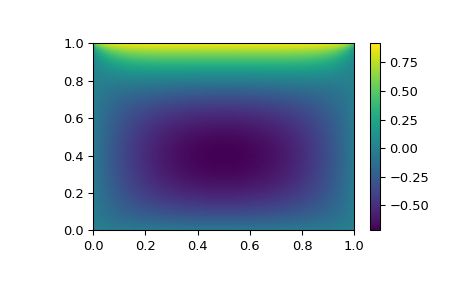
>>> import matplotlib.pyplot as plt
>>> x, y = np.mgrid[0:1:(nx*1j), 0:1:(ny*1j)]
>>> plt.pcolormesh(x, y, sol.x, shading='gouraud')
>>> plt.colorbar()
>>> plt.show()