scipy.signal.ShortTimeFFT.

频谱图

ShortTimeFFT.spectrogram(x, y=None, detr=None, *, p0=None, p1=None, k_offset=0, padding='zeros', axis=-1)

计算频谱图或交叉频谱图。

频谱图是STFT的绝对平方，即对于给定的 S[q,p] ，它是 abs(S[q,p])**2 ，因此总是非负的。对于两个STFT Sx[q,p], Sy[q,p] ，交叉频谱图定义为 Sx[q,p] * np.conj(Sx[q,p]) ，并且是复数值的。这是一个方便的函数，用于调用 stft / stft_detrend ，因此所有参数都在那里讨论。如果 y 不是 None ，它需要与 x 具有相同的形状。

参见

stft

执行短时傅里叶变换。

stft_detrend

从每个片段中减去趋势后的短时傅里叶变换。

scipy.signal.ShortTimeFFT

此方法所属的类。

示例

Try it in your browser!

以下示例展示了频率随时间变化的方波 \(f_i(t)\) （在图中以绿色虚线标记）以20 Hz采样的频谱图：

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.signal import square, ShortTimeFFT
>>> from scipy.signal.windows import gaussian
...
>>> T_x, N = 1 / 20, 1000  # 20 Hz sampling rate for 50 s signal
>>> t_x = np.arange(N) * T_x  # time indexes for signal
>>> f_i = 5e-3*(t_x - t_x[N // 3])**2 + 1  # varying frequency
>>> x = square(2*np.pi*np.cumsum(f_i)*T_x)  # the signal

所使用的高斯窗口长度为50个样本或2.5秒。参数 ``mfft=800``（过采样因子16）和 ShortTimeFFT 中的 hop 间隔2被选择以产生足够数量的点：

>>> g_std = 12  # standard deviation for Gaussian window in samples
>>> win = gaussian(50, std=g_std, sym=True)  # symmetric Gaussian wind.
>>> SFT = ShortTimeFFT(win, hop=2, fs=1/T_x, mfft=800, scale_to='psd')
>>> Sx2 = SFT.spectrogram(x)  # calculate absolute square of STFT

图的色图是按对数比例缩放的，因为功率谱密度是以dB为单位的。信号 x 的时间范围由垂直虚线标记，阴影区域标记了边界效应的存在：

>>> fig1, ax1 = plt.subplots(figsize=(6., 4.))  # enlarge plot a bit
>>> t_lo, t_hi = SFT.extent(N)[:2]  # time range of plot
>>> ax1.set_title(rf"Spectrogram ({SFT.m_num*SFT.T:g}$\,s$ Gaussian " +
...               rf"window, $\sigma_t={g_std*SFT.T:g}\,$s)")
>>> ax1.set(xlabel=f"Time $t$ in seconds ({SFT.p_num(N)} slices, " +
...                rf"$\Delta t = {SFT.delta_t:g}\,$s)",
...         ylabel=f"Freq. $f$ in Hz ({SFT.f_pts} bins, " +
...                rf"$\Delta f = {SFT.delta_f:g}\,$Hz)",
...         xlim=(t_lo, t_hi))
>>> Sx_dB = 10 * np.log10(np.fmax(Sx2, 1e-4))  # limit range to -40 dB
>>> im1 = ax1.imshow(Sx_dB, origin='lower', aspect='auto',
...                  extent=SFT.extent(N), cmap='magma')
>>> ax1.plot(t_x, f_i, 'g--', alpha=.5, label='$f_i(t)$')
>>> fig1.colorbar(im1, label='Power Spectral Density ' +
...                          r"$20\,\log_{10}|S_x(t, f)|$ in dB")
...
>>> # Shade areas where window slices stick out to the side:
>>> for t0_, t1_ in [(t_lo, SFT.lower_border_end[0] * SFT.T),
...                  (SFT.upper_border_begin(N)[0] * SFT.T, t_hi)]:
...     ax1.axvspan(t0_, t1_, color='w', linewidth=0, alpha=.3)
>>> for t_ in [0, N * SFT.T]:  # mark signal borders with vertical line
...     ax1.axvline(t_, color='c', linestyle='--', alpha=0.5)
>>> ax1.legend()
>>> fig1.tight_layout()
>>> plt.show()

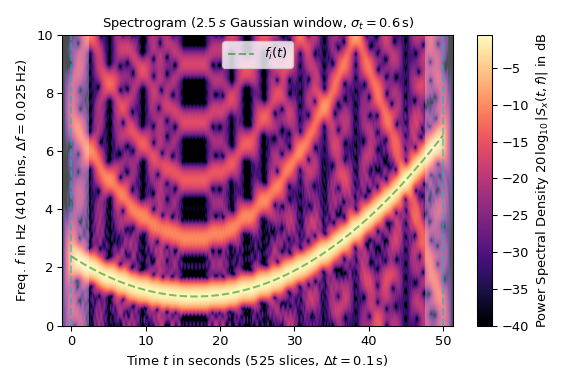
对数缩放揭示了方波的奇次谐波，这些谐波在10 Hz的奈奎斯特频率处被反射。这种混叠也是图中噪声伪影的主要来源。

Go BackOpen In Tab