scipy.signal.

ShortTimeFFT

class scipy.signal.ShortTimeFFT(win, hop, fs, *, fft_mode='onesided', mfft=None, dual_win=None, scale_to=None, phase_shift=0)

提供一个参数化的离散短时傅里叶变换（stft）及其逆变换（istft）。

stft 通过在输入信号上滑动窗口 (win) 并以 hop 增量计算连续的 FFT。它可以用来量化频谱随时间的变化。

stft 由一个复数值矩阵 S[q,p] 表示，其中第 p 列表示以时间 t[p] = p * delta_t = p * hop * T 为中心的窗口的 FFT，其中 T 是输入信号的采样间隔。第 q 行表示频率 f[q] = q * delta_f 处的值，其中 delta_f = 1 / (mfft * T) 是 FFT 的 bin 宽度。

逆STFT istft 是通过反转STFT的步骤计算的：取S[q,p]的第p个切片进行IFFT，并将结果与所谓的对偶窗口（见`dual_win`）相乘。将结果按p * `delta_t`进行移位，并将结果添加到先前移位的结果中以重构信号。如果只知道对偶窗口且STFT是可逆的，可以使用`from_dual`来实例化此类。

由于时间 t = 0 的惯例是在输入信号的第一个样本处，STFT 值通常具有负的时间槽。因此，负索引如 p_min 或 k_min 并不表示像标准 Python 索引那样从数组的末尾倒数，而是表示在 t = 0 的左侧。

更多详细信息可以在 用户指南 的 教程_stft 部分找到。

请注意，初始化器的所有参数，除了使用 scaling 的 scale_to 之外，都有相同的命名属性。

参数:

赢np.ndarray

窗口必须是一个实数或复数值的一维数组。

跳跃整数

每次窗口移动时样本的增量。

fs浮动

输入信号和窗口的采样频率。它与采样间隔 T 的关系是 T = 1 / fs。

fft_mode‘twosided’, ‘centered’, ‘onesided’, ‘onesided2X’

要使用的FFT模式（默认’onesided’）。详情请参见属性 fft_mode。

mfft: int | None

如果需要零填充的FFT，则使用FFT的长度。如果为 ``None``（默认），则使用窗口 win 的长度。

双窗口np.ndarray | None

win 的双窗口。如果设置为 None，则在需要时进行计算。

scale_to‘magnitude’, ‘psd’ | None

如果不是 None （默认），窗口函数会被缩放，因此每个STFT列代表一个’幅度’或功率谱密度（’psd’）谱。此参数将 scaling 属性设置为相同的值。详情请参见 scale_to 方法。

相移int | None

如果设置，为每个频率 f 添加一个线性相位 phase_shift / mfft * f。默认值 0 确保在第零片（其中 t=0 为中心）上没有相位偏移。更多详情请参见属性 phase_shift。

属性:

T

输入信号和窗口的采样间隔。

delta_f

STFT 频率箱的宽度。

delta_t

STFT 的时间增量。

dual_win

标准双窗口。

f

STFT 的频率值。

f_pts

频率轴上的点数。

fac_magnitude

乘以STFT值的因子，以将每个频率切片缩放到幅度谱。

fac_psd

乘以STFT值的因子，以将每个频率切片缩放到功率谱密度（PSD）。

fft_mode

使用的FFT模式（’twosided’、’centered’、’onesided’ 或 ‘onesided2X’）。

fs

输入信号和窗口的采样频率。

hop

滑动窗口中信号样本的时间增量。

invertible

检查STFT是否可逆。

k_min

STFT 可能的最小信号索引。

lower_border_end

第一个信号索引和第一个切片索引不受预填充影响。

m_num

窗口 win 中的样本数量。

m_num_mid

将窗口 win 的索引居中。

mfft

用于FFT的输入长度 - 可能大于窗口长度 m_num。

onesided_fft

如果使用单边FFT，则返回True。

p_min

最小的可能切片索引。

phase_shift

如果设置，将线性相位 phase_shift / mfft * f 添加到频率 f 的每个 FFT 切片中。

scaling

应用于窗口函数的归一化（’magnitude’、’psd’ 或 None）。

win

窗口函数作为实数或复数值的1维数组。

方法

extent(n[, axes_seq, center_bins])	返回时间-频率值的最小值和最大值。
from_dual(dual_win, hop, fs, *[, fft_mode, ...])	仅通过提供一个双窗口来实例化 ShortTimeFFT。
from_window(win_param, fs, nperseg, noverlap, *)	通过使用 get_window 实例化 ShortTimeFFT。
istft(S[, k0, k1, f_axis, t_axis])	逆短时傅里叶变换。
k_max(n)	信号结束后的第一个样本索引未被时间片触及。
nearest_k_p(k[, left])	返回满足 t[k_p] == t[p] 的最近样本索引 k_p。
p_max(n)	n 样本输入的第一个不重叠的上层时间片索引。
p_num(n)	输入信号有 n 个样本的时间片数量。
p_range(n[, p0, p1])	确定并验证切片索引范围。
scale_to(scaling)	缩放窗口以获取STFT的'magnitude'或'psd'缩放。
spectrogram(x[, y, detr, p0, p1, k_offset, ...])	计算频谱图或交叉频谱图。
stft(x[, p0, p1, k_offset, padding, axis])	执行短时傅里叶变换。
stft_detrend(x, detr[, p0, p1, k_offset, ...])	短时傅里叶变换，每个片段在变换前先减去趋势。
t(n[, p0, p1, k_offset])	输入信号有 n 个样本的 STFT 时间。
upper_border_begin(n)	受后填充影响的首个信号索引和首个切片索引。

示例

Try it in your browser!

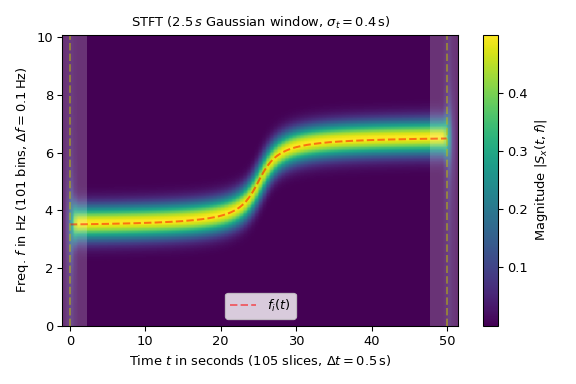
以下示例展示了频率变化的正弦波 \(f_i(t)\) 的STFT幅度（在图中以红色虚线标记）：

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import ShortTimeFFT
>>> from scipy.signal.windows import gaussian
...
>>> T_x, N = 1 / 20, 1000  # 20 Hz sampling rate for 50 s signal
>>> t_x = np.arange(N) * T_x  # time indexes for signal
>>> f_i = 1 * np.arctan((t_x - t_x[N // 2]) / 2) + 5  # varying frequency
>>> x = np.sin(2*np.pi*np.cumsum(f_i)*T_x) # the signal

所使用的高斯窗长度为50个样本，即2.5秒。ShortTimeFFT 中的参数 mfft=200 导致频谱过采样4倍：

>>> g_std = 8  # standard deviation for Gaussian window in samples
>>> w = gaussian(50, std=g_std, sym=True)  # symmetric Gaussian window
>>> SFT = ShortTimeFFT(w, hop=10, fs=1/T_x, mfft=200, scale_to='magnitude')
>>> Sx = SFT.stft(x)  # perform the STFT

在图中，信号 x 的时间范围由垂直虚线标记。注意，SFT 在 x 的时间范围之外产生值。左侧和右侧的阴影区域表示由于该区域的窗口切片不完全在 x 的时间范围内而引起的边界效应：

>>> fig1, ax1 = plt.subplots(figsize=(6., 4.))  # enlarge plot a bit
>>> t_lo, t_hi = SFT.extent(N)[:2]  # time range of plot
>>> ax1.set_title(rf"STFT ({SFT.m_num*SFT.T:g}$\,s$ Gaussian window, " +
...               rf"$\sigma_t={g_std*SFT.T}\,$s)")
>>> ax1.set(xlabel=f"Time $t$ in seconds ({SFT.p_num(N)} slices, " +
...                rf"$\Delta t = {SFT.delta_t:g}\,$s)",
...         ylabel=f"Freq. $f$ in Hz ({SFT.f_pts} bins, " +
...                rf"$\Delta f = {SFT.delta_f:g}\,$Hz)",
...         xlim=(t_lo, t_hi))
...
>>> im1 = ax1.imshow(abs(Sx), origin='lower', aspect='auto',
...                  extent=SFT.extent(N), cmap='viridis')
>>> ax1.plot(t_x, f_i, 'r--', alpha=.5, label='$f_i(t)$')
>>> fig1.colorbar(im1, label="Magnitude $|S_x(t, f)|$")
...
>>> # Shade areas where window slices stick out to the side:
>>> for t0_, t1_ in [(t_lo, SFT.lower_border_end[0] * SFT.T),
...                  (SFT.upper_border_begin(N)[0] * SFT.T, t_hi)]:
...     ax1.axvspan(t0_, t1_, color='w', linewidth=0, alpha=.2)
>>> for t_ in [0, N * SFT.T]:  # mark signal borders with vertical line:
...     ax1.axvline(t_, color='y', linestyle='--', alpha=0.5)
>>> ax1.legend()
>>> fig1.tight_layout()
>>> plt.show()

使用 istft 重建信号很简单，但请注意，应指定 x1 的长度，因为 SFT 长度以 hop 步长增加：

>>> SFT.invertible  # check if invertible
True
>>> x1 = SFT.istft(Sx, k1=N)
>>> np.allclose(x, x1)
True

可以计算信号部分的SFT：

>>> p_q = SFT.nearest_k_p(N // 2)
>>> Sx0 = SFT.stft(x[:p_q])
>>> Sx1 = SFT.stft(x[p_q:])

在将连续的STFT部分组合在一起时，需要考虑重叠部分：

>>> p0_ub = SFT.upper_border_begin(p_q)[1] - SFT.p_min
>>> p1_le = SFT.lower_border_end[1] - SFT.p_min
>>> Sx01 = np.hstack((Sx0[:, :p0_ub],
...                   Sx0[:, p0_ub:] + Sx1[:, :p1_le],
...                   Sx1[:, p1_le:]))
>>> np.allclose(Sx01, Sx)  # Compare with SFT of complete signal
True

也可以计算信号部分的 itsft：

>>> y_p = SFT.istft(Sx, N//3, N//2)
>>> np.allclose(y_p, x[N//3:N//2])
True

Go BackOpen In Tab