scipy.signal.ShortTimeFFT.

from_dual

classmethod ShortTimeFFT.from_dual(dual_win, hop, fs, *, fft_mode='onesided', mfft=None, scale_to=None, phase_shift=0)

仅通过提供一个双窗口来实例化 ShortTimeFFT。

如果一个STFT是可逆的，就有可能从给定的对偶窗口 dual_win 计算出窗口 win。所有其他参数与 ShortTimeFFT 的初始化器中的含义相同。

如 用户指南 中的 教程_stft 部分所述，可逆的STFT可以解释为时间偏移和频率调制的双窗口的级数展开。例如，级数系数 S[q,p] 属于该项，它将 dual_win 偏移了 p * delta_t 并乘以 exp( 2 * j * pi * t * q * delta_f)。

参见

from_window

通过包装 get_window 创建实例。

ShortTimeFFT

使用标准初始化器创建实例。

示例

Try it in your browser!

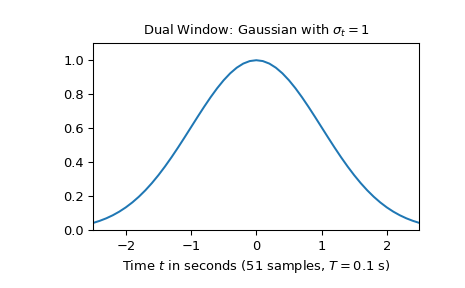
以下示例讨论了将信号分解为时间和频率偏移的高斯函数。将使用由51个样本组成的、标准偏差为1的高斯函数：

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import ShortTimeFFT
>>> from scipy.signal.windows import gaussian
...
>>> T, N = 0.1, 51
>>> d_win = gaussian(N, std=1/T, sym=True)  # symmetric Gaussian window
>>> t = T * (np.arange(N) - N//2)
...
>>> fg1, ax1 = plt.subplots()
>>> ax1.set_title(r"Dual Window: Gaussian with $\sigma_t=1$")
>>> ax1.set(xlabel=f"Time $t$ in seconds ({N} samples, $T={T}$ s)",
...        xlim=(t[0], t[-1]), ylim=(0, 1.1*max(d_win)))
>>> ax1.plot(t, d_win, 'C0-')

以下重叠了41、11和2个样本的图显示了 hop 间隔如何影响窗口 win 的形状：

>>> fig2, axx = plt.subplots(3, 1, sharex='all')
...
>>> axx[0].set_title(r"Windows for hop$\in\{10, 40, 49\}$")
>>> for c_, h_ in enumerate([10, 40, 49]):
...     SFT = ShortTimeFFT.from_dual(d_win, h_, 1/T)
...     axx[c_].plot(t + h_ * T, SFT.win, 'k--', alpha=.3, label=None)
...     axx[c_].plot(t - h_ * T, SFT.win, 'k:', alpha=.3, label=None)
...     axx[c_].plot(t, SFT.win, f'C{c_+1}',
...                     label=r"$\Delta t=%0.1f\,$s" % SFT.delta_t)
...     axx[c_].set_ylim(0, 1.1*max(SFT.win))
...     axx[c_].legend(loc='center')
>>> axx[-1].set(xlabel=f"Time $t$ in seconds ({N} samples, $T={T}$ s)",
...             xlim=(t[0], t[-1]))
>>> plt.show()

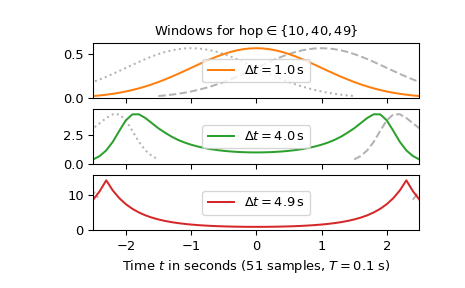
在窗口 win 中心位于 t = 0 的情况下，前一个窗口（t = -delta_t）和后一个窗口（t = delta_t）被描绘出来。可以看出，对于小的 hop 间隔，窗口紧凑且平滑，在 STFT 中具有良好的时频集中度。对于 4.9 秒的大 hop 间隔，窗口在 t = 0 附近具有较小的值，这些值未被相邻窗口的重叠覆盖，这可能导致数值不准确。此外，窗口开始和结束时的尖锐形状指向更高的带宽，导致 STFT 的时频分辨率较差。因此，hop 间隔的选择将是时频分辨率和由小 hop 大小所需的内存需求之间的折衷。

Go BackOpen In Tab