scipy.signal.

频率

scipy.signal.freqs(b, a, worN=200, plot=None)

计算模拟滤波器的频率响应。

给定模拟滤波器的 M 阶分子 b 和 N 阶分母 a，计算其频率响应:

        b[0]*(jw)**M + b[1]*(jw)**(M-1) + ... + b[M]
H(w) = ----------------------------------------------
        a[0]*(jw)**N + a[1]*(jw)**(N-1) + ... + a[N]

参数:

barray_like

线性滤波器的分子。

aarray_like

线性滤波器的分母。

worN{None, int, array_like}, 可选

如果为 None，则在响应曲线的感兴趣部分（由极点和零点位置决定）周围计算 200 个频率。如果是一个整数，则在该频率数上计算。否则，在 worN 中给出的角频率（例如，rad/s）上计算响应。

绘图可调用，可选

一个接受两个参数的可调用对象。如果提供，返回参数 w 和 h 将被传递给绘图函数。这对于在 freqs 内部绘制频率响应非常有用。

返回:

wndarray

计算 h 时的角频率。

hndarray

频率响应。

参见

freqz

计算数字滤波器的频率响应。

注释

使用 Matplotlib 的 “plot” 函数作为 plot 的可调用函数会产生意外的结果，这会绘制复数传递函数的实部，而不是幅度。尝试 lambda w, h: plot(w, abs(h))。

示例

Try it in your browser!

>>> from scipy.signal import freqs, iirfilter
>>> import numpy as np

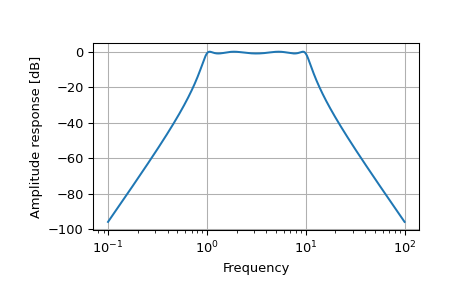
>>> b, a = iirfilter(4, [1, 10], 1, 60, analog=True, ftype='cheby1')

>>> w, h = freqs(b, a, worN=np.logspace(-1, 2, 1000))

>>> import matplotlib.pyplot as plt
>>> plt.semilogx(w, 20 * np.log10(abs(h)))
>>> plt.xlabel('Frequency')
>>> plt.ylabel('Amplitude response [dB]')
>>> plt.grid(True)
>>> plt.show()

Go BackOpen In Tab