scipy.signal.

freqz#

scipy.signal.freqz(b, a=1, worN=512, whole=False, plot=None, fs=6.283185307179586, include_nyquist=False)[源代码][源代码]#

计算数字滤波器的频率响应。

给定数字滤波器的 M 阶分子 b 和 N 阶分母 a，计算其频率响应:

            jw                 -jw              -jwM
   jw    B(e  )    b[0] + b[1]e    + ... + b[M]e
H(e  ) = ------ = -----------------------------------
            jw                 -jw              -jwN
         A(e  )    a[0] + a[1]e    + ... + a[N]e
参数:
barray_like

线性滤波器的分子。如果 b 的维度大于 1，则假定系数存储在第一个维度中，并且 b.shape[1:]、a.shape[1:] 以及频率数组的形状必须能够进行广播兼容。

aarray_like

线性滤波器的分母。如果 b 的维度大于1，则假定系数存储在第一个维度中，并且 b.shape[1:]、a.shape[1:] 以及频率数组的形状必须能够进行广播。

worN{None, int, array_like}, 可选

如果是一个整数，则在那么多频率上进行计算（默认是 N=512）。这是一个方便的替代方案:

np.linspace(0, fs if whole else fs/2, N, endpoint=include_nyquist)

使用一个适合快速傅里叶变换（FFT）计算的数字可以导致更快的计算（见注释）。

如果是一个类数组对象，则在给定的频率处计算响应。这些频率与 fs 的单位相同。

整个bool, 可选

通常，频率是从0计算到奈奎斯特频率，即fs/2（单位圆的上半部分）。如果 whole 为 True，则计算频率从0到fs。如果 worN 是类数组，则忽略此参数。

绘图可调用

一个接受两个参数的可调用对象。如果提供，返回参数 w 和 h 将被传递给绘图函数。这对于在 freqz 内部绘制频率响应非常有用。

fsfloat, 可选

数字系统的采样频率。默认值为 2*pi 弧度/样本（因此 w 从 0 到 pi）。

Added in version 1.2.0.

include_nyquistbool, 可选

如果 whole 为 False 且 worN 是整数，将 include_nyquist 设置为 True 将包含最后一个频率（奈奎斯特频率），否则将被忽略。

Added in version 1.5.0.

返回:
wndarray

计算 h 的频率，单位与 fs 相同。默认情况下，w 被归一化到范围 [0, pi)（弧度/样本）。

hndarray

频率响应，以复数表示。

参见

freqz_zpk
sosfreqz

注释

使用 Matplotlib 的 matplotlib.pyplot.plot 函数作为 plot 的可调用对象会产生意外结果，因为这会绘制复数传递函数的实部，而不是幅度。尝试使用 lambda w, h: plot(w, np.abs(h))。

当满足以下条件时，通过 (R)FFT 的直接计算用于计算频率响应：

  1. 为 worN 提供了一个整数值。

  2. worN 通过 FFT 计算速度快（即 next_fast_len(worN) 等于 worN）。

  3. 分母系数是一个单一值 (a.shape[0] == 1)。

  4. worN 至少与分子系数的长度一样长（worN >= b.shape[0]）。

  5. 如果 b.ndim > 1，那么 b.shape[-1] == 1。

对于较长的 FIR 滤波器，FFT 方法的误差可能更低，并且比等效的直接多项式计算快得多。

示例

>>> from scipy import signal
>>> import numpy as np
>>> b = signal.firwin(80, 0.5, window=('kaiser', 8))
>>> w, h = signal.freqz(b)

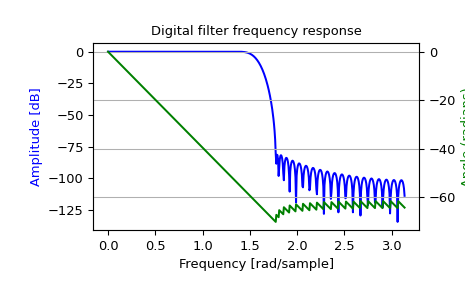
>>> import matplotlib.pyplot as plt
>>> fig, ax1 = plt.subplots()
>>> ax1.set_title('Digital filter frequency response')

>>> ax1.plot(w, 20 * np.log10(abs(h)), 'b')
>>> ax1.set_ylabel('Amplitude [dB]', color='b')
>>> ax1.set_xlabel('Frequency [rad/sample]')

>>> ax2 = ax1.twinx()
>>> angles = np.unwrap(np.angle(h))
>>> ax2.plot(w, angles, 'g')
>>> ax2.set_ylabel('Angle (radians)', color='g')
>>> ax2.grid(True)
>>> ax2.axis('tight')
>>> plt.show()
../../_images/scipy-signal-freqz-1_00_00.png

广播示例

假设我们有两个 FIR 滤波器，其系数存储在一个形状为 (2, 25) 的数组中。在这个演示中，我们将使用随机数据：

>>> rng = np.random.default_rng()
>>> b = rng.random((2, 25))

要通过一次 freqz 调用计算这两个滤波器的频率响应，我们必须传入 b.T，因为 freqz 期望第一个轴持有系数。然后，我们必须用长度为 1 的平凡维度扩展形状，以允许与频率数组进行广播。也就是说，我们传入 b.T[..., np.newaxis]，它的形状是 (25, 2, 1)：

>>> w, h = signal.freqz(b.T[..., np.newaxis], worN=1024)
>>> w.shape
(1024,)
>>> h.shape
(2, 1024)

现在，假设我们有两个传递函数，它们的分子系数相同 b = [0.5, 0.5]。两个分母的系数存储在二维数组 a 的第一个维度中:

a = [   1      1  ]
    [ -0.25, -0.5 ]

>>> b = np.array([0.5, 0.5])
>>> a = np.array([[1, 1], [-0.25, -0.5]])

只有 a 是多维的。为了使其与频率兼容以进行广播，我们在调用 freqz 时通过一个平凡的维度来扩展它：

>>> w, h = signal.freqz(b, a[..., np.newaxis], worN=1024)
>>> w.shape
(1024,)
>>> h.shape
(2, 1024)
On this page