scipy.signal.

gammatone

scipy.signal.gammatone(freq, ftype, order=None, numtaps=None, fs=None)

伽马通滤波器设计。

此函数计算 FIR 或 IIR 伽马音数字滤波器的系数 [1]。

参数:

频率浮动

滤波器的中心频率（以与 fs 相同的单位表示）。

ftype{‘fir’, ‘iir’}

该函数生成的滤波器类型。如果为 ‘fir’，函数将生成一个 N 阶 FIR 伽马通滤波器。如果为 ‘iir’，函数将生成一个 8 阶数字 IIR 滤波器，模拟为 4 阶伽马通滤波器。

顺序int, 可选

滤波器的顺序。仅在 ftype='fir' 时使用。默认值为 4，以模拟人类听觉系统。必须在 0 到 24 之间。

numtapsint, 可选

滤波器的长度。仅在 ftype='fir' 时使用。如果 fs 大于 1000，默认值为 fs*0.015；如果 fs 小于或等于 1000，默认值为 15。

fsfloat, 可选

信号的采样频率。freq 必须在 0 和 fs/2 之间。默认值为 2。

返回:

b, andarray, ndarray

滤波器的分子 (b) 和分母 (a) 多项式。

Raises:

ValueError

如果 freq 小于或等于 0 或大于或等于 fs/2，如果 ftype 不是 ‘fir’ 或 ‘iir’，如果 order 小于或等于 0 或当 ftype='fir' 时大于 24

参见

firwin

iirfilter

参考文献

[1]

Slaney, Malcolm, “帕特森-霍尔沃斯听觉滤波器组的高效实现”, Apple Computer 技术报告 35, 1993, 第3-8页, 34-39页。

示例

Try it in your browser!

16-样本 4阶 FIR 伽马通滤波器，中心频率为 440 Hz

>>> from scipy import signal
>>> signal.gammatone(440, 'fir', numtaps=16, fs=16000)
(array([ 0.00000000e+00,  2.22196719e-07,  1.64942101e-06,  4.99298227e-06,
    1.01993969e-05,  1.63125770e-05,  2.14648940e-05,  2.29947263e-05,
    1.76776931e-05,  2.04980537e-06, -2.72062858e-05, -7.28455299e-05,
   -1.36651076e-04, -2.19066855e-04, -3.18905076e-04, -4.33156712e-04]),
   [1.0])

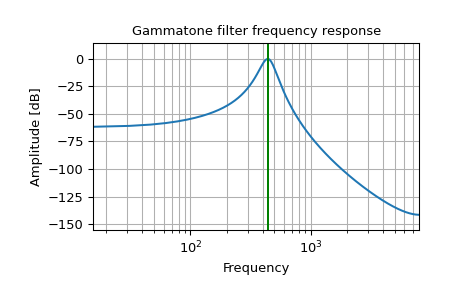
IIR Gammatone 滤波器，中心频率为 440 Hz

>>> import matplotlib.pyplot as plt
>>> import numpy as np

>>> b, a = signal.gammatone(440, 'iir', fs=16000)
>>> w, h = signal.freqz(b, a)
>>> plt.plot(w / ((2 * np.pi) / 16000), 20 * np.log10(abs(h)))
>>> plt.xscale('log')
>>> plt.title('Gammatone filter frequency response')
>>> plt.xlabel('Frequency')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.axvline(440, color='green') # cutoff frequency
>>> plt.show()

Go BackOpen In Tab