scipy.signal.

群延迟

scipy.signal.group_delay(system, w=512, whole=False, fs=6.283185307179586)

计算数字滤波器的群延迟。

群延迟通过测量信号的各个频谱分量的幅度包络被滤波器延迟的样本数来衡量。它正式定义为连续（未展开）相位的导数:

          d        jw
D(w) = - -- arg H(e)
         dw

参数:

系统数组类元组 (b, a)

滤波器传递函数的分子和分母系数。

w{None, int, array_like}, 可选

如果是一个整数，则在那么多频率上进行计算（默认是 N=512）。

如果是一个类似数组的对象，则在给定的频率下计算延迟。这些频率的单位与 fs 相同。

整个bool, 可选

通常，频率从0计算到奈奎斯特频率，即fs/2（单位圆的上半部分）。如果 whole 为 True，则计算频率从0到fs。如果 w 是类数组，则忽略此设置。

fsfloat, 可选

数字系统的采样频率。默认值为 2*pi 弧度/样本（因此 w 从 0 到 pi）。

Added in version 1.2.0.

返回:

wndarray

计算群延迟的频率，单位与 fs 相同。默认情况下，w 被归一化到范围 [0, pi)（弧度/样本）。

gdndarray

群延迟。

参见

freqz

数字滤波器的频率响应

注释

MATLAB 中类似的函数称为 grpdelay。

如果传递函数 \(H(z)\) 在单位圆上有零点或极点，相应频率的群延迟是未定义的。当这种情况发生时，会发出警告，并将这些频率的群延迟设置为0。

关于群延迟的数值计算细节，请参考 [1] 或 [2]。

Added in version 0.16.0.

参考文献

[1]

Richard G. Lyons, “理解数字信号处理, 第三版”, 第830页。

[2]

Julius O. Smith III, “群延迟的数值计算”，见“音频应用的数字滤波器介绍”，在线书籍，2007年，https://ccrma.stanford.edu/~jos/fp/Numerical_Computation_Group_Delay.html

示例

Try it in your browser!

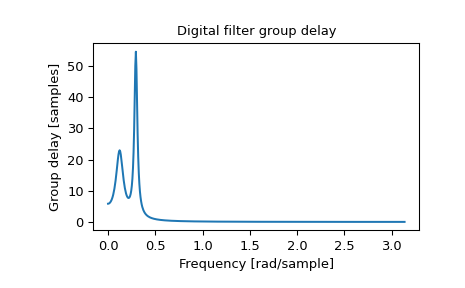
>>> from scipy import signal
>>> b, a = signal.iirdesign(0.1, 0.3, 5, 50, ftype='cheby1')
>>> w, gd = signal.group_delay((b, a))

>>> import matplotlib.pyplot as plt
>>> plt.title('Digital filter group delay')
>>> plt.plot(w, gd)
>>> plt.ylabel('Group delay [samples]')
>>> plt.xlabel('Frequency [rad/sample]')
>>> plt.show()

Go BackOpen In Tab