scipy.signal.

iirdesign#

scipy.signal.iirdesign(wp, ws, gpass, gstop, analog=False, ftype='ellip', output='ba', fs=None)[源代码][源代码]#

完成IIR数字和模拟滤波器设计。

给定通带和阻带频率及增益，为给定的基本类型构造最小阶数的模拟或数字IIR滤波器。返回分子、分母（’ba’）、极点-零点（’zpk’）或二阶节（’sos’）形式的输出。

参数:
wp, ws浮点数或类似数组，形状为 (2,)

通带和阻带边缘频率。可能的值是标量（用于低通和高通滤波器）或范围（用于带通和带阻滤波器）。对于数字滤波器，这些值与 fs 的单位相同。默认情况下，fs 是 2 个半周期/样本，因此这些值在 0 到 1 之间归一化，其中 1 是奈奎斯特频率。例如：

  • 低通滤波器: wp = 0.2, ws = 0.3

  • 高通滤波器: wp = 0.3, ws = 0.2

  • 带通滤波器: wp = [0.2, 0.5], ws = [0.1, 0.6]

  • 带阻滤波器: wp = [0.1, 0.6], ws = [0.2, 0.5]

对于模拟滤波器，wp 和 ws 是角频率（例如，rad/s）。注意，对于带通和带阻滤波器，通带必须严格位于阻带内或反之。

gpass浮动

通带中的最大损耗（dB）。

gstop浮动

阻带中的最小衰减（dB）。

模拟bool, 可选

当为 True 时，返回一个模拟滤波器，否则返回一个数字滤波器。

ftypestr, 可选

要设计的IIR滤波器的类型：

  • Butterworth : ‘butter’

  • 切比雪夫 I 型 : ‘cheby1’

  • 切比雪夫 II : ‘cheby2’

  • Cauer/椭圆：’ellip’

输出{‘ba’, ‘zpk’, ‘sos’}, 可选

输出过滤形式：

  • 二级章节（推荐）：’sos’

  • 分子/分母 (默认) : ‘ba’

  • pole-zero : ‘zpk’

通常推荐使用二阶节 (‘sos’) 形式，因为推导分子/分母形式 (‘ba’) 的系数会遇到数值不稳定性问题。出于向后兼容性的原因，默认形式是分子/分母形式 (‘ba’)，其中 ‘ba’ 中的 ‘b’ 和 ‘a’ 指的是常用的系数名称。

注意：使用二阶节形式（’sos’）有时会带来额外的计算成本：因此，对于数据密集型用例，建议也研究分子/分母形式（’ba’）。

fsfloat, 可选

数字系统的采样频率。

Added in version 1.2.0.

返回:
b, andarray, ndarray

IIR 滤波器的分子多项式（b）和分母多项式（a）。仅当 output='ba' 时返回。

z, p, kndarray, ndarray, float

IIR 滤波器传递函数的零点、极点和系统增益。仅在 output='zpk' 时返回。

sosndarray

IIR 滤波器的二阶节表示。仅在 output='sos' 时返回。

参见

butter

使用阶数和临界点的滤波器设计

cheby1, cheby2, ellip, bessel
buttord

从通带和阻带规格中找到阶数和临界点

cheb1ord, cheb2ord, ellipord
iirfilter

使用阶数和临界频率进行一般滤波器设计

注释

'sos' 输出参数在 0.16.0 版本中被添加。

示例

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> import matplotlib.ticker

>>> wp = 0.2
>>> ws = 0.3
>>> gpass = 1
>>> gstop = 40

>>> system = signal.iirdesign(wp, ws, gpass, gstop)
>>> w, h = signal.freqz(*system)

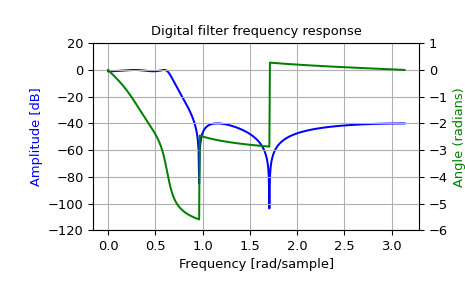
>>> fig, ax1 = plt.subplots()
>>> ax1.set_title('Digital filter frequency response')
>>> ax1.plot(w, 20 * np.log10(abs(h)), 'b')
>>> ax1.set_ylabel('Amplitude [dB]', color='b')
>>> ax1.set_xlabel('Frequency [rad/sample]')
>>> ax1.grid(True)
>>> ax1.set_ylim([-120, 20])
>>> ax2 = ax1.twinx()
>>> angles = np.unwrap(np.angle(h))
>>> ax2.plot(w, angles, 'g')
>>> ax2.set_ylabel('Angle (radians)', color='g')
>>> ax2.grid(True)
>>> ax2.axis('tight')
>>> ax2.set_ylim([-6, 1])
>>> nticks = 8
>>> ax1.yaxis.set_major_locator(matplotlib.ticker.LinearLocator(nticks))
>>> ax2.yaxis.set_major_locator(matplotlib.ticker.LinearLocator(nticks))
../../_images/scipy-signal-iirdesign-1.png
On this page