scipy.signal.

sweep_poly

scipy.signal.sweep_poly(t, poly, phi=0)

频率扫描余弦发生器，具有时间依赖的频率。

此函数生成一个正弦函数，其瞬时频率随时间变化。时间 t 处的频率由多项式 poly 给出。

参数:

tndarray

评估波形的时间点。

多边形1-D array_like 或 numpy.poly1d 的实例

所需频率表示为多项式。如果 poly 是一个长度为 n 的列表或 ndarray，那么 poly 的元素是多项式的系数，瞬时频率为

f(t) = poly[0]*t**(n-1) + poly[1]*t**(n-2) + ... + poly[n-1]

如果 poly 是 numpy.poly1d 的一个实例，那么瞬时频率为

f(t) = poly(t)

phifloat, 可选

相位偏移，单位为度，默认值：0。

返回:

sweep_polyndarray

一个包含信号在 t 时刻评估值的 numpy 数组，具有请求的时变频率。更准确地说，该函数返回 cos(phase + (pi/180)*phi)，其中 phase 是从 0 到 t 的 2 * pi * f(t) 的积分；f(t) 如上定义。

参见

chirp

注释

Added in version 0.8.0.

如果 poly 是一个长度为 n 的列表或 ndarray，那么 poly 的元素是多项式的系数，瞬时频率为：

f(t) = poly[0]*t**(n-1) + poly[1]*t**(n-2) + ... + poly[n-1]

如果 poly 是 numpy.poly1d 的一个实例，那么瞬时频率为：

f(t) = poly(t)

最后，输出 s 是：

cos(phase + (pi/180)*phi)

其中 phase 是从 0 到 t 的 2 * pi * f(t) 的积分，f(t) 如上定义。

示例

Try it in your browser!

计算具有瞬时频率的波形:

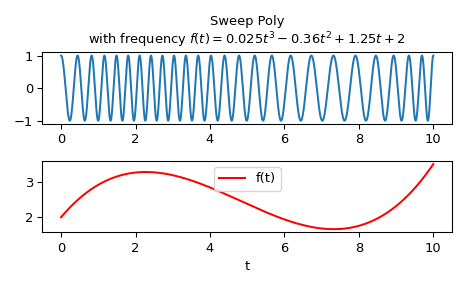
f(t) = 0.025*t**3 - 0.36*t**2 + 1.25*t + 2

在区间 0 <= t <= 10 上。

>>> import numpy as np
>>> from scipy.signal import sweep_poly
>>> p = np.poly1d([0.025, -0.36, 1.25, 2.0])
>>> t = np.linspace(0, 10, 5001)
>>> w = sweep_poly(t, p)

绘制它：

>>> import matplotlib.pyplot as plt
>>> plt.subplot(2, 1, 1)
>>> plt.plot(t, w)
>>> plt.title("Sweep Poly\nwith frequency " +
...           "$f(t) = 0.025t^3 - 0.36t^2 + 1.25t + 2$")
>>> plt.subplot(2, 1, 2)
>>> plt.plot(t, p(t), 'r', label='f(t)')
>>> plt.legend()
>>> plt.xlabel('t')
>>> plt.tight_layout()
>>> plt.show()

Go BackOpen In Tab