scipy.signal.

chirp

scipy.signal.chirp(t, f0, t1, f1, method='linear', phi=0, vertex_zero=True)

频率扫描余弦波发生器。

在下文中，’Hz’ 应解释为 ‘每单位周期’；这里没有要求单位是一秒。重要的区别在于旋转的单位是周期，而不是弧度。同样，t 可以是空间的测量，而不是时间。

参数:

tarray_like

评估波形的时间点。

f0浮动

频率（例如 Hz）在时间 t=0 时。

t1浮动

指定 f1 的时间。

f1浮动

波形在时间 t1 处的频率（例如 Hz）。

方法{‘线性’, ‘二次’, ‘对数’, ‘双曲’}, 可选

频率扫描的类型。如果没有给出，则假设为 线性 。有关更多详细信息，请参见下面的注释。

phifloat, 可选

相位偏移，以度为单位。默认值为0。

vertex_zerobool, 可选

仅当 method 为 ‘quadratic’ 时使用此参数。它决定抛物线的顶点，即频率图，是在 t=0 还是 t=t1。

返回:

yndarray

一个包含在 t 时刻评估的信号的 numpy 数组，具有请求的时变频率。更准确地说，该函数返回 cos(phase + (pi/180)*phi)，其中 phase 是从 0 到 t 的 2*pi*f(t) 的积分。f(t) 定义如下。

参见

sweep_poly

注释

method 有四种选项。以下公式给出了由 chirp() 生成的信号的瞬时频率（以赫兹为单位）。为了方便起见，也可以使用下面显示的较短名称。

linear, lin, li:

f(t) = f0 + (f1 - f0) * t / t1

二次的, 四边形的, q:

频率 f(t) 的图形是一条通过 (0, f0) 和 (t1, f1) 的抛物线。默认情况下，抛物线的顶点位于 (0, f0)。如果 vertex_zero 为 False，则顶点位于 (t1, f1)。公式为：

如果 vertex_zero 为 True:

f(t) = f0 + (f1 - f0) * t**2 / t1**2

否则：

f(t) = f1 - (f1 - f0) * (t1 - t)**2 / t1**2

要使用更一般的二次函数，或任意多项式，请使用函数 scipy.signal.sweep_poly。

对数的, 对数, 对数:

f(t) = f0 * (f1/f0)**(t/t1)

f0 和 f1 必须为非零且符号相同。

这个信号也被称为几何或指数啁啾。

双曲的, hyp:

f(t) = f0*f1*t1 / ((f0 - f1)*t + f1*t1)

f0 和 f1 必须为非零值。

示例

Try it in your browser!

以下内容将用于示例中：

>>> import numpy as np
>>> from scipy.signal import chirp, spectrogram
>>> import matplotlib.pyplot as plt

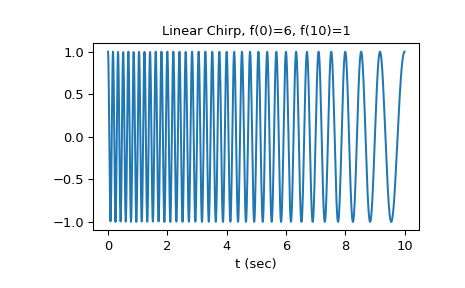
在第一个示例中，我们将绘制一个从6 Hz到1 Hz的线性啁啾波形，持续时间为10秒：

>>> t = np.linspace(0, 10, 1500)
>>> w = chirp(t, f0=6, f1=1, t1=10, method='linear')
>>> plt.plot(t, w)
>>> plt.title("Linear Chirp, f(0)=6, f(10)=1")
>>> plt.xlabel('t (sec)')
>>> plt.show()

对于剩余的示例，我们将使用更高频率范围，并使用 scipy.signal.spectrogram 展示结果。我们将使用一个采样率为 7200 Hz 的 4 秒间隔。

>>> fs = 7200
>>> T = 4
>>> t = np.arange(0, int(T*fs)) / fs

我们将使用此函数在每个示例中绘制频谱图。

>>> def plot_spectrogram(title, w, fs):
...     ff, tt, Sxx = spectrogram(w, fs=fs, nperseg=256, nfft=576)
...     fig, ax = plt.subplots()
...     ax.pcolormesh(tt, ff[:145], Sxx[:145], cmap='gray_r',
...                   shading='gouraud')
...     ax.set_title(title)
...     ax.set_xlabel('t (sec)')
...     ax.set_ylabel('Frequency (Hz)')
...     ax.grid(True)
...

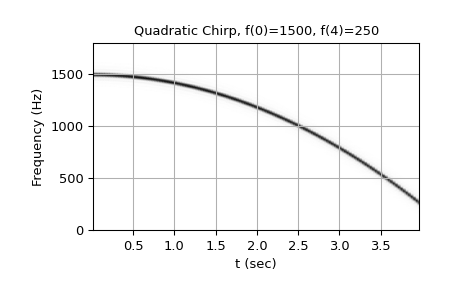
从1500 Hz到250 Hz的二次啁啾（频率抛物线曲线的顶点在t=0处）：

>>> w = chirp(t, f0=1500, f1=250, t1=T, method='quadratic')
>>> plot_spectrogram(f'Quadratic Chirp, f(0)=1500, f({T})=250', w, fs)
>>> plt.show()

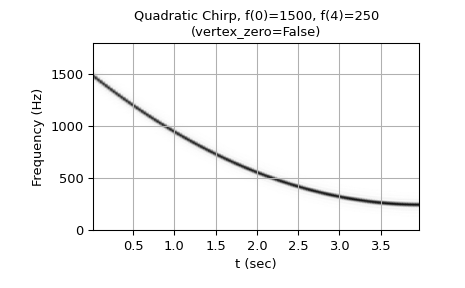
从1500 Hz到250 Hz的二次啁啾（频率抛物线曲线的顶点在t=T处）：

>>> w = chirp(t, f0=1500, f1=250, t1=T, method='quadratic',
...           vertex_zero=False)
>>> plot_spectrogram(f'Quadratic Chirp, f(0)=1500, f({T})=250\n' +
...                  '(vertex_zero=False)', w, fs)
>>> plt.show()

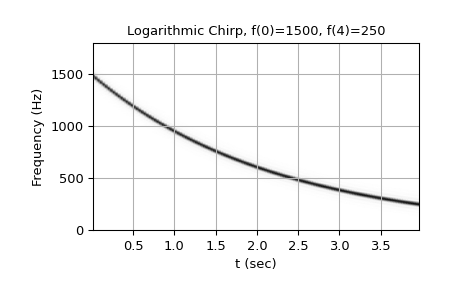
从1500 Hz到250 Hz的对数啁啾：

>>> w = chirp(t, f0=1500, f1=250, t1=T, method='logarithmic')
>>> plot_spectrogram(f'Logarithmic Chirp, f(0)=1500, f({T})=250', w, fs)
>>> plt.show()

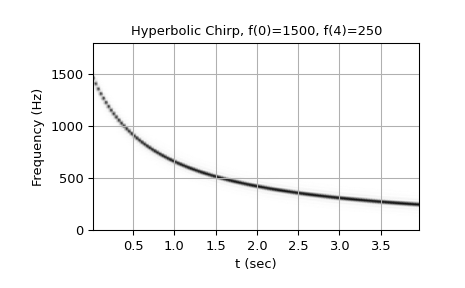
从1500 Hz到250 Hz的双曲线啁啾声：

>>> w = chirp(t, f0=1500, f1=250, t1=T, method='hyperbolic')
>>> plot_spectrogram(f'Hyperbolic Chirp, f(0)=1500, f({T})=250', w, fs)
>>> plt.show()

Go BackOpen In Tab