scipy.spatial.

Delaunay

class scipy.spatial.Delaunay(points, furthest_site=False, incremental=False, qhull_options=None)

N 维中的 Delaunay 三角剖分。

Added in version 0.9.

参数:

点浮点数的 ndarray，形状为 (npoints, ndim)

用于三角剖分的点坐标

furthest_sitebool, 可选

是否计算最远点Delaunay三角剖分。默认值：False

Added in version 0.12.0.

增量bool, 可选

允许逐步添加新点。这会占用一些额外资源。

qhull_optionsstr, 可选

传递给 Qhull 的额外选项。详情请参阅 Qhull 手册。选项 “Qt” 始终启用。默认值：ndim > 4 时为 “Qbb Qc Qz Qx Q12”，否则为 “Qbb Qc Qz Q12”。增量模式省略 “Qz”。

Added in version 0.12.0.

属性:

点双精度 ndarray，形状为 (npoints, ndim)

输入点的坐标。

单纯形整数 ndarray，形状为 (nsimplex, ndim+1)

形成三角剖分中单纯形的点的索引。对于2-D，点的方向是逆时针的。

邻居整数 ndarray，形状为 (nsimplex, ndim+1)

每个单纯形的邻居单纯形的索引。第 k 个邻居与第 k 个顶点相对。对于边界上的单纯形，-1 表示没有邻居。

方程式双精度 ndarray，形状为 (nsimplex, ndim+2)

[normal, offset] 形成抛物面上面的面的超平面方程（更多信息请参见 Qhull 文档）。

抛物面缩放, 抛物面平移浮动

额外抛物面维度的缩放和平移（更多信息请参见 Qhull 文档）。

transform双精度 ndarray，形状为 (nsimplex, ndim+1, ndim)

从 x 到重心坐标 c 的仿射变换。

vertex_to_simplex整数 ndarray，形状为 (npoints,)

查找数组，从一个顶点，到它所属的某个单纯形。

convex_hullint 类型的 ndarray，形状为 (nfaces, ndim)

形成点集凸包的面片的顶点。

共面int 类型的 ndarray，形状为 (ncoplanar, 3)

共面点的索引以及对应的最近面的索引和最近顶点的索引。共面点是由于数值精度问题而未被包含在三角剖分中的输入点。

如果未指定选项“Qc”，则不计算此列表。

Added in version 0.12.0.

vertex_neighbor_vertices两个整数 ndarray 的元组；(indptr, indices)

顶点的相邻顶点。

furthest_site

如果这是最远点三角剖分则为True，否则为False。

Added in version 1.4.0.

方法

add_points(points[, restart])	处理一组额外的新的要点。
close()	完成增量处理。
find_simplex(self, xi[, bruteforce, tol])	找到包含给定点的单纯形。
lift_points(self, x)	提升点指向 Qhull 抛物面。
plane_distance(self, xi)	计算从所有单纯形到点 xi 的超平面距离。

Raises:

QhullError

当 Qhull 遇到错误条件时引发，例如在未启用解决选项时的几何退化。

ValueError

如果输入的是一个不兼容的数组，则会引发此错误。

注释

镶嵌是通过使用 Qhull 库 Qhull 库 计算的。

备注

除非你传入 Qhull 选项 “QJ”，否则 Qhull 不能保证每个输入点都出现在 Delaunay 三角剖分中。被省略的点列在 coplanar 属性中。

示例

Try it in your browser!

一组点的三角剖分：

>>> import numpy as np
>>> points = np.array([[0, 0], [0, 1.1], [1, 0], [1, 1]])
>>> from scipy.spatial import Delaunay
>>> tri = Delaunay(points)

我们可以绘制它：

>>> import matplotlib.pyplot as plt
>>> plt.triplot(points[:,0], points[:,1], tri.simplices)
>>> plt.plot(points[:,0], points[:,1], 'o')
>>> plt.show()

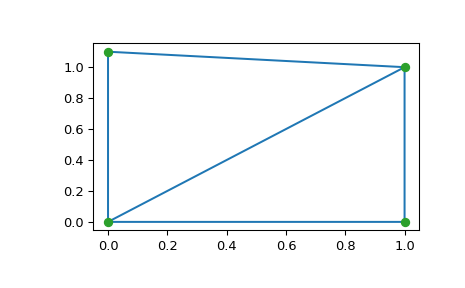
形成三角剖分的两个三角形的点索引和坐标：

>>> tri.simplices
array([[2, 3, 0],                 # may vary
       [3, 1, 0]], dtype=int32)

请注意，根据舍入误差的处理方式，单纯形的顺序可能与上述不同。

>>> points[tri.simplices]
array([[[ 1. ,  0. ],            # may vary
        [ 1. ,  1. ],
        [ 0. ,  0. ]],
       [[ 1. ,  1. ],
        [ 0. ,  1.1],
        [ 0. ,  0. ]]])

三角形 0 是三角形 1 的唯一邻居，并且它与三角形 1 的顶点 1 相对：

>>> tri.neighbors[1]
array([-1,  0, -1], dtype=int32)
>>> points[tri.simplices[1,1]]
array([ 0. ,  1.1])

我们可以找出哪些三角形的点在其中：

>>> p = np.array([(0.1, 0.2), (1.5, 0.5), (0.5, 1.05)])
>>> tri.find_simplex(p)
array([ 1, -1, 1], dtype=int32)

数组中返回的整数是对应点所在的单纯形的索引。如果返回 -1，则该点不在任何单纯形中。请注意，以下示例中的快捷方式仅对有效点正确工作，因为无效点会导致返回 -1，而 -1 本身是列表中最后一个单纯形的有效索引。

>>> p_valids = np.array([(0.1, 0.2), (0.5, 1.05)])
>>> tri.simplices[tri.find_simplex(p_valids)]
array([[3, 1, 0],                 # may vary
       [3, 1, 0]], dtype=int32)

我们也可以为这些点计算三角形1中的重心坐标：

>>> b = tri.transform[1,:2].dot(np.transpose(p - tri.transform[1,2]))
>>> np.c_[np.transpose(b), 1 - b.sum(axis=0)]
array([[ 0.1       ,  0.09090909,  0.80909091],
       [ 1.5       , -0.90909091,  0.40909091],
       [ 0.5       ,  0.5       ,  0.        ]])

第一个点的坐标均为正值，这意味着它确实位于三角形内部。第三个点在一条边上，因此其第三个坐标为空。

Go BackOpen In Tab