scipy.spatial.cKDTree.

query_ball_tree

cKDTree.query_ball_tree(self, other, r, p=2., eps=0)

找到 self 和 other 之间所有距离最多为 r 的点对

参数:

其他cKDTree 实例

包含用于搜索的点的树。

r浮动

最大距离必须是正数。

pfloat, 可选

使用哪种 Minkowski 范数。p 必须满足条件 1 <= p <= 无穷大。如果可能发生溢出，较大的有限 p 可能会导致 ValueError。

epsfloat, 可选

近似搜索。如果树的分支的最近点比 r/(1+eps) 更远，则不会探索这些分支，并且如果分支的最远点比 r * (1+eps) 更近，则这些分支会批量添加。eps 必须是非负的。

返回:

结果列表的列表

对于这棵树的每个元素 self.data[i]，results[i] 是其在 other.data 中邻居的索引列表。

示例

Try it in your browser!

你可以在两个kd树之间搜索所有距离内的点对：

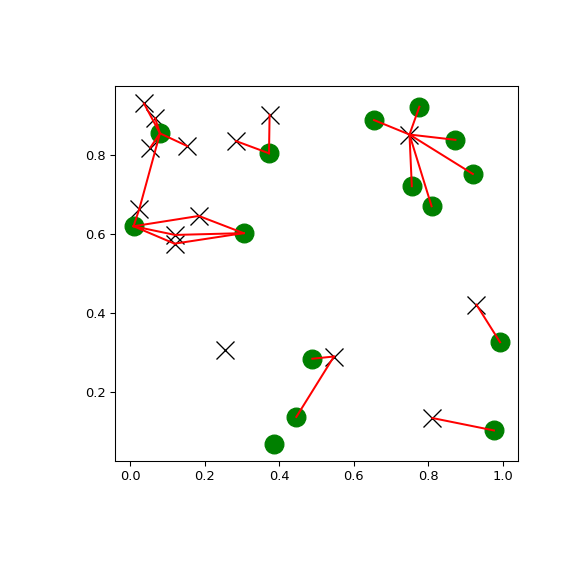
>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.spatial import cKDTree
>>> rng = np.random.default_rng()
>>> points1 = rng.random((15, 2))
>>> points2 = rng.random((15, 2))
>>> plt.figure(figsize=(6, 6))
>>> plt.plot(points1[:, 0], points1[:, 1], "xk", markersize=14)
>>> plt.plot(points2[:, 0], points2[:, 1], "og", markersize=14)
>>> kd_tree1 = cKDTree(points1)
>>> kd_tree2 = cKDTree(points2)
>>> indexes = kd_tree1.query_ball_tree(kd_tree2, r=0.2)
>>> for i in range(len(indexes)):
...     for j in indexes[i]:
...         plt.plot([points1[i, 0], points2[j, 0]],
...             [points1[i, 1], points2[j, 1]], "-r")
>>> plt.show()

Go BackOpen In Tab