scipy.special.airy#

scipy.special.airy(z, out=None) = <ufunc 'airy'>#

Airy 函数及其导数。

参数:

zarray_like: 实数或复数参数。
出ndarray 的元组，可选: 函数值的可选输出数组

返回:

Ai, Aip, Bi, Bip4元组，可以是标量或ndarray: Airy 函数 Ai 和 Bi，以及它们的导数 Aip 和 Bip。

参见

airye: 指数缩放的Airy函数。

注释

Airy 函数 Ai 和 Bi 是两个独立的解。

\[y''(x) = x y(x).\]

对于实数 z 在 [-10, 10] 范围内，计算通过调用 Cephes [1] airy 例程进行，该例程对小的 z 使用幂级数求和，对大的 z 使用有理最小最大近似。

超出此范围，将使用AMOS [2] 的 zairy 和 zbiry 例程。它们在 \(|z| < 1\) 时使用幂级数计算，对于较大的 z`（其中 :math:`t equiv 2 z^{3/2}/3），则使用以下关系式与修正贝塞尔函数相关联：

\[ \begin{align}\begin{aligned}Ai(z) = \frac{1}{\pi \sqrt{3}} K_{1/3}(t)\\Ai'(z) = -\frac{z}{\pi \sqrt{3}} K_{2/3}(t)\\Bi(z) = \sqrt{\frac{z}{3}} \left(I_{-1/3}(t) + I_{1/3}(t) \right)\\Bi'(z) = \frac{z}{\sqrt{3}} \left(I_{-2/3}(t) + I_{2/3}(t)\right)\end{aligned}\end{align} \]

参考文献

[1]

Cephes 数学函数库, http://www.netlib.org/cephes/

[2]

Donald E. Amos, “AMOS, 一个用于复数参数和非负阶贝塞尔函数的便携式软件包”, http://netlib.org/amos/

示例

计算区间 [-15, 5] 上的 Airy 函数。

>>> import numpy as np
>>> from scipy import special
>>> x = np.linspace(-15, 5, 201)
>>> ai, aip, bi, bip = special.airy(x)

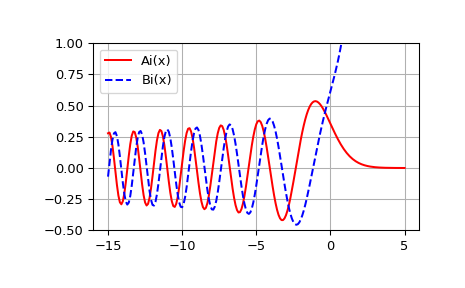
绘制 Ai(x) 和 Bi(x)。

>>> import matplotlib.pyplot as plt
>>> plt.plot(x, ai, 'r', label='Ai(x)')
>>> plt.plot(x, bi, 'b--', label='Bi(x)')
>>> plt.ylim(-0.5, 1.0)
>>> plt.grid()
>>> plt.legend(loc='upper left')
>>> plt.show()