scipy.special.

gegenbauer

scipy.special.gegenbauer(n, alpha, monic=False)

Gegenbauer（超球面）多项式。

定义为的解

\[(1 - x^2)\frac{d^2}{dx^2}C_n^{(\alpha)} - (2\alpha + 1)x\frac{d}{dx}C_n^{(\alpha)} + n(n + 2\alpha)C_n^{(\alpha)} = 0\]

对于 \(\alpha > -1/2\)；\(C_n^{(\alpha)}\) 是一个次数为 \(n\) 的多项式。

参数:

n整数

多项式的次数。

alpha浮动

参数，必须大于 -0.5。

monicbool, 可选

如果 True，将首项系数缩放为 1。默认是 False。

返回:

Corthopoly1d

Gegenbauer 多项式。

注释

多项式 \(C_n^{(\alpha)}\) 在区间 \([-1,1]\) 上关于权函数 \((1 - x^2)^{(\alpha - 1/2)}\) 是正交的。

示例

Try it in your browser!

>>> import numpy as np
>>> from scipy import special
>>> import matplotlib.pyplot as plt

我们可以使用 gegenbauer 函数将变量 p 初始化为一个 Gegenbauer 多项式，并在点 x = 1 处进行评估。

>>> p = special.gegenbauer(3, 0.5, monic=False)
>>> p
poly1d([ 2.5,  0. , -1.5,  0. ])
>>> p(1)
1.0

要在区间 (-3, 3) 中的不同点 x 处评估 p，只需将数组 x 传递给 p，如下所示：

>>> x = np.linspace(-3, 3, 400)
>>> y = p(x)

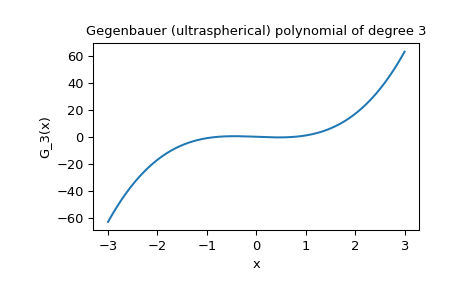
然后我们可以使用 matplotlib.pyplot 来可视化 x, y。

>>> fig, ax = plt.subplots()
>>> ax.plot(x, y)
>>> ax.set_title("Gegenbauer (ultraspherical) polynomial of degree 3")
>>> ax.set_xlabel("x")
>>> ax.set_ylabel("G_3(x)")
>>> plt.show()

Go BackOpen In Tab