scipy.special.iti0k0

scipy.special.iti0k0(x, out=None) = <ufunc 'iti0k0'>

零阶修正贝塞尔函数的积分。

计算积分

\[\begin{split}\int_0^x I_0(t) dt \\ \int_0^x K_0(t) dt.\end{split}\]

更多关于 \(I_0\) 和 \(K_0\) 的信息，请参见 i0 和 k0。

参数:

xarray_like

要计算积分的值。

出ndarrays 的元组，可选

函数结果的可选输出数组。

返回:

ii0标量或ndarray

i0 的积分

ik0标量或ndarray

k0 的积分

参考文献

[1]

S. Zhang and J.M. Jin, “Computation of Special Functions”, Wiley 1996

示例

Try it in your browser!

在一点处评估函数。

>>> from scipy.special import iti0k0
>>> int_i, int_k = iti0k0(1.)
>>> int_i, int_k
(1.0865210970235892, 1.2425098486237771)

在多个点上评估函数。

>>> import numpy as np
>>> points = np.array([0., 1.5, 3.])
>>> int_i, int_k = iti0k0(points)
>>> int_i, int_k
(array([0.        , 1.80606937, 6.16096149]),
 array([0.        , 1.39458246, 1.53994809]))

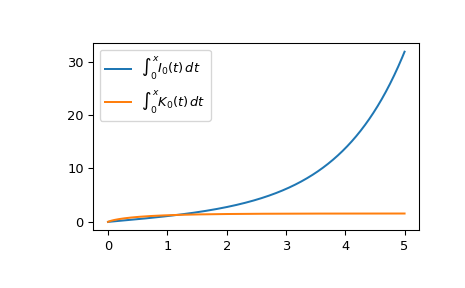
绘制从0到5的函数。

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> x = np.linspace(0., 5., 1000)
>>> int_i, int_k = iti0k0(x)
>>> ax.plot(x, int_i, label=r"$\int_0^x I_0(t)\,dt$")
>>> ax.plot(x, int_k, label=r"$\int_0^x K_0(t)\,dt$")
>>> ax.legend()
>>> plt.show()

Go BackOpen In Tab