scipy.special.sici#

scipy.special.sici(x, out=None) = <ufunc 'sici'>#

正弦和余弦积分。

正弦积分是

\[\int_0^x \frac{\sin{t}}{t}dt\]

余弦积分是

\[\gamma + \log(x) + \int_0^x \frac{\cos{t} - 1}{t}dt\]

其中 \(\gamma\) 是欧拉常数，\(\log\) 是对数的主分支 [1]。

参数:

xarray_like: 计算正弦和余弦积分的实数或复数点。
出ndarray 的元组，可选: 函数结果的可选输出数组

返回:

si标量或ndarray: 在 x 处的正弦积分
ci标量或ndarray: 余弦积分在 x 处

参见

shichi: 双曲正弦和余弦积分。
exp1: 指数积分 E1。
expi: 指数积分 Ei。

注释

对于 x < 0 的实际参数，ci 是余弦积分的实部。在这些点上，ci(x) 和 ci(x + 0j) 相差一个因子 1j*pi。

对于实数参数，该函数通过调用 Cephes 的 [2] sici 例程来计算。对于复数参数，该算法基于 Mpmath 的 [3] si 和 ci 例程。

参考文献

[1] (1,2)

Milton Abramowitz 和 Irene A. Stegun 编。《带有公式、图表和数学表格的数学函数手册》。纽约：Dover，1972年。（参见第5.2节。）

[2]

Cephes 数学函数库, http://www.netlib.org/cephes/

[3]

Fredrik Johansson 等人。“mpmath: 一个用于任意精度浮点运算的 Python 库”（版本 0.19） http://mpmath.org/

示例

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.special import sici, exp1

sici 接受实数或复数输入：

>>> sici(2.5)
(1.7785201734438267, 0.2858711963653835)
>>> sici(2.5 + 3j)
((4.505735874563953+0.06863305018999577j),
(0.0793644206906966-2.935510262937543j))

对于右半平面中的 z，正弦和余弦积分与指数积分 E1（在 SciPy 中实现为 scipy.special.exp1）相关联。

Si(z) = (E1(i*z) - E1(-i*z))/2i + pi/2
Ci(z) = -(E1(i*z) + E1(-i*z))/2

参见 [1] （方程 5.2.21 和 5.2.23）。

我们可以验证这些关系：

>>> z = 2 - 3j
>>> sici(z)
((4.54751388956229-1.3991965806460565j),
(1.408292501520851+2.9836177420296055j))

>>> (exp1(1j*z) - exp1(-1j*z))/2j + np.pi/2  # Same as sine integral
(4.54751388956229-1.3991965806460565j)

>>> -(exp1(1j*z) + exp1(-1j*z))/2            # Same as cosine integral
(1.408292501520851+2.9836177420296055j)

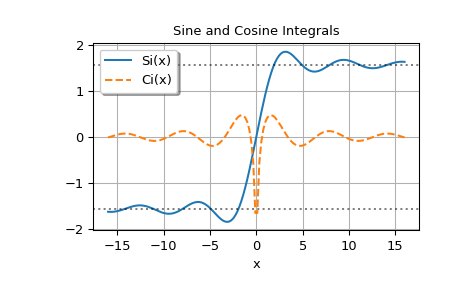
绘制在实轴上评估的函数；虚线水平线位于 pi/2 和 -pi/2 处：

>>> x = np.linspace(-16, 16, 150)
>>> si, ci = sici(x)

>>> fig, ax = plt.subplots()
>>> ax.plot(x, si, label='Si(x)')
>>> ax.plot(x, ci, '--', label='Ci(x)')
>>> ax.legend(shadow=True, framealpha=1, loc='upper left')
>>> ax.set_xlabel('x')
>>> ax.set_title('Sine and Cosine Integrals')
>>> ax.axhline(np.pi/2, linestyle=':', alpha=0.5, color='k')
>>> ax.axhline(-np.pi/2, linestyle=':', alpha=0.5, color='k')
>>> ax.grid(True)
>>> plt.show()