scipy.special.

sinc

scipy.special.sinc(x)

返回归一化的sinc函数。

sinc 函数对于任何参数 \(x\ne 0\) 等于 \(\sin(\pi x)/(\pi x)\)。sinc(0) 取极限值 1，使得 sinc 不仅处处连续，而且无限可微。

备注

注意在定义中使用的 pi 的归一化因子。这是信号处理中最常用的定义。使用 sinc(x / np.pi) 来获得未归一化的 sinc 函数 \(\sin(x)/x\)，这在数学中更为常见。

参数:

xndarray

用于计算 sinc(x) 的值的数组（可能是多维的）。

返回:

出ndarray

sinc(x)，其形状与输入相同。

注释

名称 sinc 是 “sine cardinal” 或 “sinus cardinalis” 的缩写。

sinc 函数在各种信号处理应用中使用，包括抗锯齿、构建 Lanczos 重采样滤波器和插值。

对于离散时间信号的带限插值，理想的插值核与sinc函数成正比。

参考文献

[1]

Weisstein, Eric W. “Sinc 函数.” 来自 MathWorld–A Wolfram 网络资源。 https://mathworld.wolfram.com/SincFunction.html

[2]

维基百科，“Sinc 函数”，https://en.wikipedia.org/wiki/Sinc_function

示例

Try it in your browser!

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> x = np.linspace(-4, 4, 41)
>>> np.sinc(x)
 array([-3.89804309e-17,  -4.92362781e-02,  -8.40918587e-02, # may vary
        -8.90384387e-02,  -5.84680802e-02,   3.89804309e-17,
        6.68206631e-02,   1.16434881e-01,   1.26137788e-01,
        8.50444803e-02,  -3.89804309e-17,  -1.03943254e-01,
        -1.89206682e-01,  -2.16236208e-01,  -1.55914881e-01,
        3.89804309e-17,   2.33872321e-01,   5.04551152e-01,
        7.56826729e-01,   9.35489284e-01,   1.00000000e+00,
        9.35489284e-01,   7.56826729e-01,   5.04551152e-01,
        2.33872321e-01,   3.89804309e-17,  -1.55914881e-01,
       -2.16236208e-01,  -1.89206682e-01,  -1.03943254e-01,
       -3.89804309e-17,   8.50444803e-02,   1.26137788e-01,
        1.16434881e-01,   6.68206631e-02,   3.89804309e-17,
        -5.84680802e-02,  -8.90384387e-02,  -8.40918587e-02,
        -4.92362781e-02,  -3.89804309e-17])

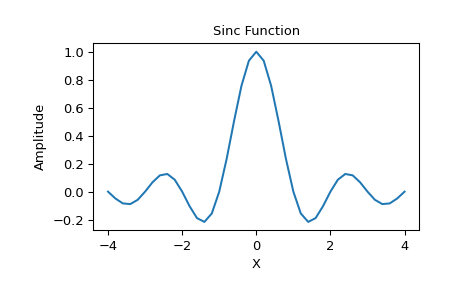
>>> plt.plot(x, np.sinc(x))
[<matplotlib.lines.Line2D object at 0x...>]
>>> plt.title("Sinc Function")
Text(0.5, 1.0, 'Sinc Function')
>>> plt.ylabel("Amplitude")
Text(0, 0.5, 'Amplitude')
>>> plt.xlabel("X")
Text(0.5, 0, 'X')
>>> plt.show()

Go BackOpen In Tab