scipy.special.

ynp_zeros

scipy.special.ynp_zeros(n, nt)

计算整数阶贝塞尔函数导数 Yn’(x) 的零点。

计算函数 \(Y_n'(x)\) 在区间 \((0, \infty)\) 上的 nt 个零点。零点按升序返回。

参数:

n整数

贝塞尔函数的顺序

nt整数

返回的零的数量

返回:

ndarray

贝塞尔导数函数的前 nt 个零点。

参见

yvp

参考文献

[1]

张善杰和金建铭。《特殊函数的计算》，John Wiley and Sons, 1996年，第5章。https://people.sc.fsu.edu/~jburkardt/f77_src/special_functions/special_functions.html

示例

Try it in your browser!

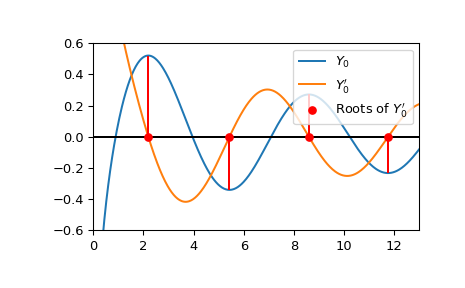
计算贝塞尔函数第二类0阶的导数的前四个根 \(Y_0'\)。

>>> from scipy.special import ynp_zeros
>>> ynp_zeros(0, 4)
array([ 2.19714133,  5.42968104,  8.59600587, 11.74915483])

绘制 \(Y_0\)、\(Y_0'\) 并确认从视觉上可以看出 \(Y_0'\) 的根位于 \(Y_0\) 的局部极值处。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.special import yn, ynp_zeros, yvp
>>> zeros = ynp_zeros(0, 4)
>>> xmax = 13
>>> x = np.linspace(0, xmax, 500)
>>> fig, ax = plt.subplots()
>>> ax.plot(x, yn(0, x), label=r'$Y_0$')
>>> ax.plot(x, yvp(0, x, 1), label=r"$Y_0'$")
>>> ax.scatter(zeros, np.zeros((4, )), s=30, c='r',
...            label=r"Roots of $Y_0'$", zorder=5)
>>> for root in zeros:
...     y0_extremum =  yn(0, root)
...     lower = min(0, y0_extremum)
...     upper = max(0, y0_extremum)
...     ax.vlines(root, lower, upper, color='r')
>>> ax.hlines(0, 0, xmax, color='k')
>>> ax.set_ylim(-0.6, 0.6)
>>> ax.set_xlim(0, xmax)
>>> plt.legend()
>>> plt.show()

Go BackOpen In Tab