scipy.stats.

logrank#

scipy.stats.logrank(x, y, alternative='two-sided')[源代码][源代码]#

通过对数秩检验比较两个样本的生存分布。

参数:

x, y类似数组或CensoredData

基于经验生存函数进行比较的样本。

替代方案{‘双侧’, ‘小于’, ‘大于’}, 可选

定义备择假设。

零假设是两组（例如 X 和 Y）的生存分布是相同的。

以下备选假设 [4] 可用（默认是 ‘双侧’）：

‘双侧’: 两组的生存分布不相同。
‘less’: 群体 X 的生存受到青睐：在某些时候，群体 X 的失效率函数低于群体 Y 的失效率函数。
‘greater’: 群体 Y 的生存被偏好: 群体 X 的失效率函数在某些时刻大于群体 Y 的失效率函数。

返回:

resLogRankResult

一个包含属性的对象：

统计浮点数 ndarray: 计算的统计量（定义如下）。其大小是大多数其他对数秩检验实现返回的大小平方根。
p值浮点数 ndarray: 测试的计算p值。

参见

scipy.stats.ecdf

注释

logrank 检验 [1] 比较了在零假设下，两个样本来自同一分布时，观察到的事件数与预期的事件数。该统计量是

\[Z_i = \frac{\sum_{j=1}^J(O_{i,j}-E_{i,j})}{\sqrt{\sum_{j=1}^J V_{i,j}}} \rightarrow \mathcal{N}(0,1)\]

哪里

\[E_{i,j} = O_j \frac{N_{i,j}}{N_j}, \qquad V_{i,j} = E_{i,j} \left(\frac{N_j-O_j}{N_j}\right) \left(\frac{N_j-N_{i,j}}{N_j-1}\right),\]

\(i\) 表示组（即它可以取值 \(x\) 或 \(y\)，或者它可以被省略以指代合并样本），\(j\) 表示时间（事件发生的时间），\(N\) 是在事件发生前处于风险中的受试者数量，\(O\) 是在该时间点观察到的事件数量。

statistic \(Z_x\) 由 logrank 返回的是许多其他实现返回的统计量的（带符号的）平方根。在零假设下，\(Z_x**2\) 渐近地服从自由度为1的卡方分布。因此，\(Z_x\) 渐近地服从标准正态分布。使用 \(Z_x\) 的优点是保留了符号信息（即观察到的事件数量是否倾向于少于或大于零假设下的预期数量），从而使 scipy.stats.logrank 能够提供单侧备择假设。

参考文献

[1]

Mantel N. “生存数据的评估及其考虑中产生的两个新的秩次统计量。” 《癌症化疗报告》，50(3):163-170，PMID: 5910392，1966

[2]

Bland, Altman, “The logrank test”, BMJ, 328:1073, DOI:10.1136/bmj.328.7447.1073, 2004

[3]

“Logrank 检验”，维基百科，https://en.wikipedia.org/wiki/Logrank_test

[4]

Brown, Mark. “对数秩检验中方差的选取。” 《生物计量学》71.1 (1984): 65-74.

[5]

Klein, John P., 和 Melvin L. Moeschberger. 生存分析：处理截尾和截断数据的技术. 第1230卷. 纽约: Springer, 2003.

示例

参考文献 [2] 比较了两类复发性恶性胶质瘤患者的生存时间。以下样本记录了每位患者参与研究的时间（周数）。使用 scipy.stats.CensoredData 类是因为数据是右删失的：未删失的观测对应于观察到的死亡，而删失的观测对应于患者因其他原因离开研究。

>>> from scipy import stats
>>> x = stats.CensoredData(
...     uncensored=[6, 13, 21, 30, 37, 38, 49, 50,
...                 63, 79, 86, 98, 202, 219],
...     right=[31, 47, 80, 82, 82, 149]
... )
>>> y = stats.CensoredData(
...     uncensored=[10, 10, 12, 13, 14, 15, 16, 17, 18, 20, 24, 24,
...                 25, 28,30, 33, 35, 37, 40, 40, 46, 48, 76, 81,
...                 82, 91, 112, 181],
...     right=[34, 40, 70]
... )

我们可以如下计算并可视化两组的经验生存函数。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> ax = plt.subplot()
>>> ecdf_x = stats.ecdf(x)
>>> ecdf_x.sf.plot(ax, label='Astrocytoma')
>>> ecdf_y = stats.ecdf(y)
>>> ecdf_y.sf.plot(ax, label='Glioblastoma')
>>> ax.set_xlabel('Time to death (weeks)')
>>> ax.set_ylabel('Empirical SF')
>>> plt.legend()
>>> plt.show()

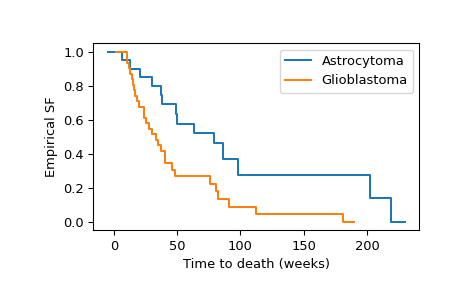
../../_images/scipy-stats-logrank-1_00_00.png

对经验生存函数的视觉检查表明，两组之间的生存时间往往不同。为了正式评估这种差异在1%水平上是否显著，我们使用对数秩检验。

>>> res = stats.logrank(x=x, y=y)
>>> res.statistic
-2.73799
>>> res.pvalue
0.00618

p 值小于 1%，因此我们可以认为数据是支持备择假设的证据，即两个生存函数之间存在差异。