scipy.stats.

monte_carlo_test

scipy.stats.monte_carlo_test(data, rvs, statistic, *, vectorized=None, n_resamples=9999, batch=None, alternative='two-sided', axis=0)

执行蒙特卡罗假设检验。

data 包含一个样本或一个或多个样本的序列。rvs 指定在零假设下 data 中样本的分布。对于给定的 data，其 statistic 值与蒙特卡罗零分布进行比较：使用 rvs 生成的每组 n_resamples 样本集的统计值。这给出了 p 值，即在零假设下观察到如此极端的检验统计值的概率。

参数:

数据类数组或类数组序列

一个观测数组或观测数组的序列。

rvs可调用对象或可调用对象的元组

一个可调用对象或可调用对象序列，用于在零假设下生成随机变量。rvs 的每个元素都必须是一个可调用对象，它接受关键字参数 size``（例如 ``rvs(size=(m, n))）并返回该形状的 N 维数组样本。如果 rvs 是一个序列，rvs 中的可调用对象数量必须与 data 中的样本数量匹配，即 len(rvs) == len(data)。如果 rvs 是一个单独的可调用对象，则 data 被视为单个样本。

统计可调用

要计算假设检验p值的统计量。statistic 必须是一个可调用的函数，它接受一个样本（例如 statistic(sample)）或 len(rvs) 个独立的样本（例如如果 rvs 包含两个可调用对象且 data 包含两个样本，则为 statistic(samples1, sample2)）并返回结果统计量。如果 vectorized 设置为 True，statistic 还必须接受一个关键字参数 axis，并且能够向量化地沿着 data 中样本的提供 axis 计算统计量。

矢量化bool, 可选

如果 vectorized 设置为 False，statistic 将不会传递关键字参数 axis，并且预期仅计算 1D 样本的统计量。如果为 True，statistic 将传递关键字参数 axis，并且预期在传递 ND 样本数组时沿 axis 计算统计量。如果为 None``（默认），如果 `statistic` 的参数包含 `axis`，则 `vectorized` 将设置为 ``True。使用向量化统计量通常会减少计算时间。

n_resamplesint, 默认值: 9999

从 rvs 的每个可调用对象中抽取的样本数量。等效地，在零假设下用作蒙特卡罗零分布的统计值数量。

批处理int, 可选

每次调用 statistic 时处理的蒙特卡洛样本数量。内存使用量为 O( batch * sample.size[axis] )。默认值为 None，在这种情况下 batch 等于 n_resamples。

替代方案{‘双侧’, ‘小于’, ‘大于’}

计算p值的备择假设。对于每个备择假设，p值定义如下。

• 'greater' : 空分布中大于或等于检验统计量观测值的百分比。

• 'less' : 空分布中小于或等于检验统计量观测值的百分比。

• 'two-sided' : 上述p值中较小者的两倍。

轴int, 默认值: 0

计算统计量时所依据的 data`（或 `data 中的每个样本）的轴。

返回:

resMonteCarloTestResult

一个带有属性的对象：

统计浮点数或ndarray

观察到的 数据 的检验统计量。

p值浮点数或ndarray

给定替代假设的p值。

null_distributionndarray

在零假设下生成的检验统计量的值。

警告

p值是通过计算零分布中与统计量的观测值同样极端或更极端的元素数量来计算的。由于使用了有限精度算术，一些统计函数在理论值完全相等时返回数值上不同的值。在某些情况下，这可能导致计算的p值出现较大误差。monte_carlo_test 通过将零分布中与检验统计量的观测值“接近”（在非精确数据类型的浮点数epsilon的100倍相对容差范围内）的元素视为等于检验统计量的观测值来防止这种情况。然而，建议用户检查零分布，以评估这种比较方法是否合适，如果不合适，则手动计算p值。

参考文献

[1]

B. Phipson and G. K. Smyth. “Permutation P-values Should Never Be Zero: Calculating Exact P-values When Permutations Are Randomly Drawn.” Statistical Applications in Genetics and Molecular Biology 9.1 (2010).

示例

Try it in your browser!

假设我们希望测试一个小样本是否来自正态分布。我们决定将样本的偏度作为检验统计量，并且我们认为p值为0.05具有统计显著性。

>>> import numpy as np
>>> from scipy import stats
>>> def statistic(x, axis):
...     return stats.skew(x, axis)

在收集完数据后，我们计算检验统计量的观测值。

>>> rng = np.random.default_rng()
>>> x = stats.skewnorm.rvs(a=1, size=50, random_state=rng)
>>> statistic(x, axis=0)
0.12457412450240658

为了确定如果样本是从正态分布中抽取的，观察到如此极端的偏度值的概率，我们可以进行蒙特卡罗假设检验。该检验将从其正态分布中随机抽取许多样本，计算每个样本的偏度，并将我们原始的偏度与这个分布进行比较，以确定一个近似的p值。

>>> from scipy.stats import monte_carlo_test
>>> # because our statistic is vectorized, we pass `vectorized=True`
>>> rvs = lambda size: stats.norm.rvs(size=size, random_state=rng)
>>> res = monte_carlo_test(x, rvs, statistic, vectorized=True)
>>> print(res.statistic)
0.12457412450240658
>>> print(res.pvalue)
0.7012

在零假设下，获得小于或等于观测值的检验统计量的概率约为70%。这大于我们选择的5%的阈值，因此我们不能认为这是反对零假设的有力证据。

请注意，这个p值基本上与 scipy.stats.skewtest 的结果相匹配，后者依赖于基于样本偏度的检验统计量的渐近分布。

>>> stats.skewtest(x).pvalue
0.6892046027110614

这种渐近近似对于小样本量无效，但 monte_carlo_test 可以用于任何大小的样本。

>>> x = stats.skewnorm.rvs(a=1, size=7, random_state=rng)
>>> # stats.skewtest(x) would produce an error due to small sample
>>> res = monte_carlo_test(x, rvs, statistic, vectorized=True)

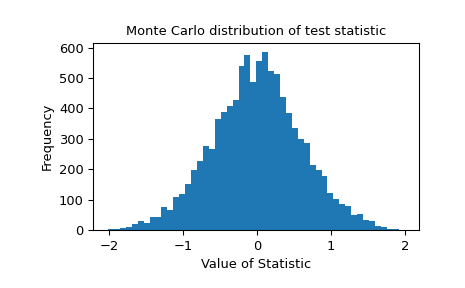
提供了测试统计量的蒙特卡罗分布，以供进一步研究。

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> ax.hist(res.null_distribution, bins=50)
>>> ax.set_title("Monte Carlo distribution of test statistic")
>>> ax.set_xlabel("Value of Statistic")
>>> ax.set_ylabel("Frequency")
>>> plt.show()

Go BackOpen In Tab