scipy.stats.

skewtest

scipy.stats.skewtest(a, axis=0, nan_policy='propagate', alternative='two-sided', *, keepdims=False)

测试偏度是否与正态分布不同。

此函数测试零假设，即样本所来自的总体的偏度与相应的正态分布的偏度相同。

参数:

a数组

要测试的数据。必须包含至少八个观测值。

轴int 或 None, 默认值: 0

如果是一个整数，表示输入数据中要计算统计量的轴。输入数据的每个轴切片（例如行）的统计量将出现在输出的相应元素中。如果为 None，则在计算统计量之前会将输入数据展平。

nan_policy{‘propagate’, ‘omit’, ‘raise’}

定义如何处理输入的 NaN。

• propagate: 如果在计算统计量的轴切片（例如行）中存在 NaN，则输出的相应条目将为 NaN。

• omit: 在执行计算时，NaN 将被省略。如果在计算统计量的轴切片中剩余的数据不足，则输出的相应条目将为 NaN。

• raise: 如果存在 NaN，将引发 ValueError。

替代方案{‘双侧’, ‘小于’, ‘大于’}, 可选

定义备择假设。默认是’双侧’。以下选项可用：

• ‘双侧’: 样本基础分布的偏度与正态分布的偏度不同（即0）

• ‘less’: 样本基础分布的偏度小于正态分布的偏度

• ‘greater’: 样本基础分布的偏度大于正态分布的偏度

Added in version 1.7.0.

keepdimsbool, 默认值: False

如果设置为True，被减少的轴将作为尺寸为1的维度保留在结果中。通过此选项，结果将正确地与输入数组进行广播。

返回:

统计浮动

此测试的计算z分数。

p值浮动

假设检验的p值。

注释

样本量必须至少为8。

从 SciPy 1.9 开始，np.matrix 输入（不推荐用于新代码）在计算执行前被转换为 np.ndarray。在这种情况下，输出将是一个标量或适当形状的 np.ndarray，而不是一个 2D 的 np.matrix。同样，虽然掩码数组的掩码元素被忽略，但输出将是一个标量或 np.ndarray，而不是一个 mask=False 的掩码数组。

参考文献

[1]

R. B. D’Agostino, A. J. Belanger and R. B. D’Agostino Jr., “A suggestion for using powerful and informative tests of normality”, American Statistician 44, pp. 316-321, 1990.

[2]

Shapiro, S. S., & Wilk, M. B. (1965). 正态性的方差分析检验（完整样本）。《生物统计学》, 52(3/4), 591-611.

[3]

B. Phipson and G. K. Smyth. “Permutation P-values Should Never Be Zero: Calculating Exact P-values When Permutations Are Randomly Drawn.” Statistical Applications in Genetics and Molecular Biology 9.1 (2010).

示例

Try it in your browser!

假设我们希望通过测量来推断医学研究中成年男性体重是否不符合正态分布 [2]。体重（磅）记录在下面的数组 x 中。

>>> import numpy as np
>>> x = np.array([148, 154, 158, 160, 161, 162, 166, 170, 182, 195, 236])

来自 [1] 的偏度检验首先基于样本偏度计算一个统计量。

>>> from scipy import stats
>>> res = stats.skewtest(x)
>>> res.statistic
2.7788579769903414

因为正态分布的偏度为零，所以从正态分布中抽取的样本的这一统计量的值往往较低。

测试是通过将统计量的观测值与零分布进行比较来进行的：零分布是指在权重是从正态分布中抽取的零假设下得出的统计量值的分布。

在这个测试中，对于非常大的样本，统计量的零分布是标准正态分布。

>>> import matplotlib.pyplot as plt
>>> dist = stats.norm()
>>> st_val = np.linspace(-5, 5, 100)
>>> pdf = dist.pdf(st_val)
>>> fig, ax = plt.subplots(figsize=(8, 5))
>>> def st_plot(ax):  # we'll reuse this
...     ax.plot(st_val, pdf)
...     ax.set_title("Skew Test Null Distribution")
...     ax.set_xlabel("statistic")
...     ax.set_ylabel("probability density")
>>> st_plot(ax)
>>> plt.show()

比较通过p值量化：零分布中与统计量的观测值同样极端或更极端的值的比例。在双侧检验中，零分布中大于观测统计量的元素和零分布中小于观测统计量负值的元素都被视为“更极端”。

>>> fig, ax = plt.subplots(figsize=(8, 5))
>>> st_plot(ax)
>>> pvalue = dist.cdf(-res.statistic) + dist.sf(res.statistic)
>>> annotation = (f'p-value={pvalue:.3f}\n(shaded area)')
>>> props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
>>> _ = ax.annotate(annotation, (3, 0.005), (3.25, 0.02), arrowprops=props)
>>> i = st_val >= res.statistic
>>> ax.fill_between(st_val[i], y1=0, y2=pdf[i], color='C0')
>>> i = st_val <= -res.statistic
>>> ax.fill_between(st_val[i], y1=0, y2=pdf[i], color='C0')
>>> ax.set_xlim(-5, 5)
>>> ax.set_ylim(0, 0.1)
>>> plt.show()

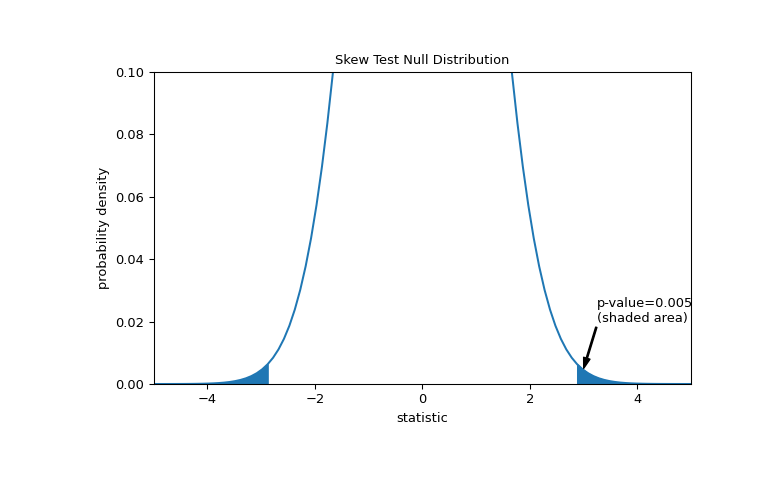
>>> res.pvalue
0.005455036974740185

如果 p 值是“小”的——也就是说，如果从正态分布的总体中抽取数据产生如此极端的统计值的概率很低——这可能被视为反对零假设而支持备择假设的证据：权重并非来自正态分布。请注意：

• 反之则不然；也就是说，测试并不用于为零假设提供证据。

• 被认为是“小”的值的阈值是在分析数据之前应做出的选择 [3] ，同时考虑到假阳性（错误地拒绝零假设）和假阴性（未能拒绝错误的零假设）的风险。

请注意，标准正态分布提供了零分布的渐近近似；它仅对具有许多观测值的样本准确。对于像我们这样的小样本，scipy.stats.monte_carlo_test 可能会提供更准确（尽管是随机的）的精确 p 值近似。

>>> def statistic(x, axis):
...     # get just the skewtest statistic; ignore the p-value
...     return stats.skewtest(x, axis=axis).statistic
>>> res = stats.monte_carlo_test(x, stats.norm.rvs, statistic)
>>> fig, ax = plt.subplots(figsize=(8, 5))
>>> st_plot(ax)
>>> ax.hist(res.null_distribution, np.linspace(-5, 5, 50),
...         density=True)
>>> ax.legend(['aymptotic approximation\n(many observations)',
...            'Monte Carlo approximation\n(11 observations)'])
>>> plt.show()

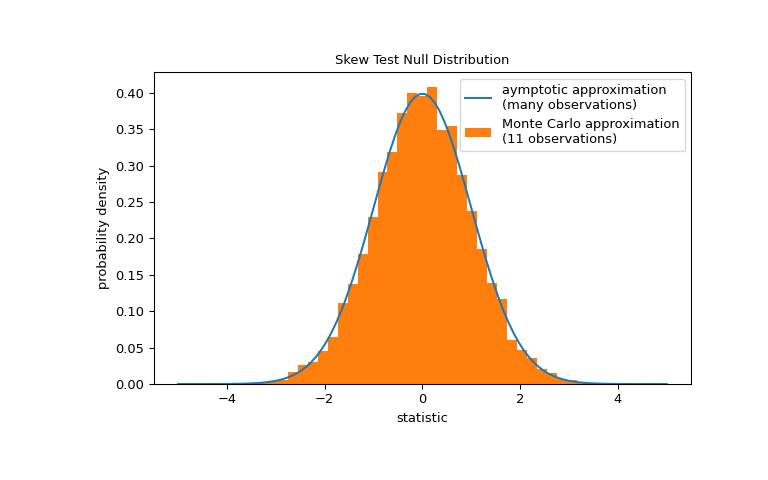
>>> res.pvalue
0.0062  # may vary

在这种情况下，渐近近似和蒙特卡罗近似相当接近，即使对于我们的小样本也是如此。

Go BackOpen In Tab