scipy.stats.

probplot

scipy.stats.probplot(x, sparams=(), dist='norm', fit=True, plot=None, rvalue=False)

计算概率图的分位数，并可选择显示该图。

生成样本数据与指定理论分布（默认是正态分布）的分位数的概率图。probplot 可以选择计算数据的最佳拟合线，并使用 Matplotlib 或给定的绘图函数绘制结果。

参数:

xarray_like

probplot 创建图表所依据的样本/响应数据。

sparamstuple, 可选

特定分布的形状参数（形状参数加上位置和尺度）。

diststr 或 stats.distributions 实例，可选

分布或分布函数名称。默认值为 ‘norm’，用于正态概率图。看起来足够像 stats.distributions 实例的对象（即它们具有 ppf 方法）也可以接受。

拟合bool, 可选

如果为 True（默认），则将最小二乘回归（最佳拟合）线拟合到样本数据。

绘图对象，可选

如果给出，绘制分位数。如果给出且 fit 为 True，还会绘制最小二乘拟合。plot 是一个必须具有“plot”和“text”方法的对象。可以使用 matplotlib.pyplot 模块或 Matplotlib Axes 对象，或者具有相同方法的自定义对象。默认值为 None，这意味着不创建绘图。

右值bool, 可选

如果提供了 plot 并且 fit 为 True，将 rvalue 设置为 True 会在图中包含决定系数。默认为 False。

返回:

(osm, osr)ndarrays 的元组

理论分位数元组（osm，或顺序统计中位数）和有序响应（osr）。osr 只是输入 x 的简单排序。有关如何计算 osm 的详细信息，请参见注释部分。

(斜率, 截距, r)浮点数元组，可选

包含最小二乘拟合结果的元组，如果这是由 probplot 执行的。r 是决定系数的平方根。如果 fit=False 且 plot=None，则不返回此元组。

注释

即使给出了 plot，probplot 也不会显示或保存图形；调用 probplot 后应使用 plt.show() 或 plt.savefig('figname.png')。

probplot 生成一个概率图，这不应与 Q-Q 图或 P-P 图混淆。Statsmodels 有更多此类功能，参见 statsmodels.api.ProbPlot。

用于理论分位数（概率图的水平轴）的公式是Filliben的估计:

quantiles = dist.ppf(val), for

        0.5**(1/n),                  for i = n
  val = (i - 0.3175) / (n + 0.365),  for i = 2, ..., n-1
        1 - 0.5**(1/n),              for i = 1

其中 i 表示第 i 个有序值，n 是值的总数。

示例

Try it in your browser!

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> nsample = 100
>>> rng = np.random.default_rng()

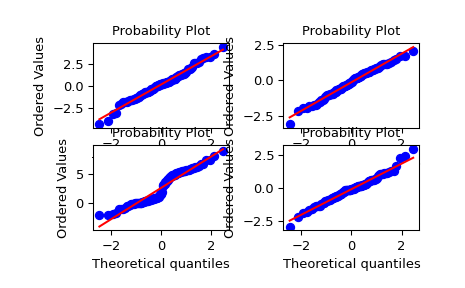
自由度较小的 t 分布：

>>> ax1 = plt.subplot(221)
>>> x = stats.t.rvs(3, size=nsample, random_state=rng)
>>> res = stats.probplot(x, plot=plt)

具有较大自由度的t分布：

>>> ax2 = plt.subplot(222)
>>> x = stats.t.rvs(25, size=nsample, random_state=rng)
>>> res = stats.probplot(x, plot=plt)

两个正态分布的混合，带有广播：

>>> ax3 = plt.subplot(223)
>>> x = stats.norm.rvs(loc=[0,5], scale=[1,1.5],
...                    size=(nsample//2,2), random_state=rng).ravel()
>>> res = stats.probplot(x, plot=plt)

标准正态分布：

>>> ax4 = plt.subplot(224)
>>> x = stats.norm.rvs(loc=0, scale=1, size=nsample, random_state=rng)
>>> res = stats.probplot(x, plot=plt)

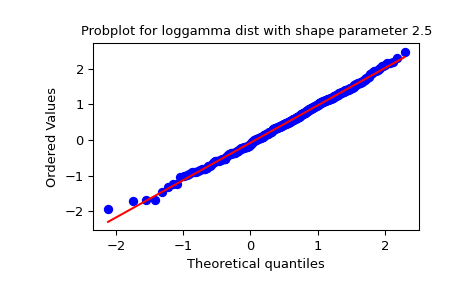
使用 dist 和 sparams 关键字生成一个新的具有对数伽马分布的图形：

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> x = stats.loggamma.rvs(c=2.5, size=500, random_state=rng)
>>> res = stats.probplot(x, dist=stats.loggamma, sparams=(2.5,), plot=ax)
>>> ax.set_title("Probplot for loggamma dist with shape parameter 2.5")

使用 Matplotlib 显示结果：

>>> plt.show()

Go BackOpen In Tab