scipy.stats.sampling.

SimpleRatioUniforms#

class scipy.stats.sampling.SimpleRatioUniforms(dist, *, mode=None, pdf_area=1, domain=None, cdf_at_mode=None, random_state=None)#

简单均匀比率 (SROU) 方法。

SROU 基于比率-均匀方法，该方法使用通用不等式来构造一个（通用）边界矩形。它适用于 T(x) = -1/sqrt(x) 的 T-凹分布。该方法的主要优点是设置速度快。如果在需要反复生成具有不同形状参数的分布的小到中等样本的情况下，这可能是有益的。在这种情况下，NumericalInverseHermite 或 NumericalInversePolynomial 的设置步骤将导致性能不佳。

参数:
dist对象

具有 pdf 方法的类的一个实例。

  • pdf: 分布的PDF。PDF的签名预期为：def pdf(self, x: float) -> float。即，PDF应接受一个Python浮点数并返回一个Python浮点数。它不需要积分为1，即PDF不需要归一化。如果未归一化，`pdf_area`应设置为PDF下的面积。

模式float, 可选

(精确) 分布的模式。当模式为 None 时，将使用一个缓慢的数值例程来近似它。默认值为 None。

pdf_areafloat, 可选

PDF 下的面积。可选地，可以在增加拒绝常数的情况下传递 PDF 下面积的上限。默认为 1。

领域长度为2的列表或元组，可选

对分布的支持。默认是 None。当 None 时：

  • 如果分布对象 dist 提供了 support 方法，它将用于设置分布的域。

  • 否则，支持集被假定为 \((-\infty, \infty)\)。

cdf_at_modefloat, 可选

在模式处的CDF。它可以被提供以提高算法的性能。当在模式处给出CDF时，拒绝常数减半。默认是 None。

random_state{None, int,}

用于生成均匀随机数流的底层 NumPy 随机数生成器的 NumPy 随机数生成器或种子。如果 random_state 是 None（或 np.random），则使用 numpy.random.RandomState 单例。如果 random_state 是整数，则使用一个新的 RandomState 实例，并以 random_state 为种子。如果 random_state 已经是 Generator 或 RandomState 实例，则使用该实例。

方法

rvs([size, random_state])

来自发行版的示例。

set_random_state([random_state])

设置底层均匀随机数生成器。

参考文献

[1]

UNU.RAN 参考手册，第5.3.16节，“SROU - 简单比率-均匀方法”，http://statmath.wu.ac.at/software/unuran/doc/unuran.html#SROU

[2]

Leydold, Josef. “一个用于连续和离散单变量 T-凹分布的简单通用生成器。” ACM 数学软件汇刊 (TOMS) 27.1 (2001): 66-82

[3]

Leydold, Josef. “通过广义比率-均匀方法的短通用生成器。” 《计算数学》72.243 (2003): 1453-1471

示例

>>> from scipy.stats.sampling import SimpleRatioUniforms
>>> import numpy as np

假设我们有一个正态分布：

>>> class StdNorm:
...     def pdf(self, x):
...         return np.exp(-0.5 * x**2)

请注意，PDF 没有积分到 1。我们可以在生成器初始化期间传递 PDF 下的确切面积或 PDF 下确切面积的上限。此外，建议传递分布的模式以加快设置速度：

>>> urng = np.random.default_rng()
>>> dist = StdNorm()
>>> rng = SimpleRatioUniforms(dist, mode=0,
...                           pdf_area=np.sqrt(2*np.pi),
...                           random_state=urng)

现在，我们可以使用 rvs 方法从分布中生成样本：

>>> rvs = rng.rvs(10)

如果模式下的CDF可用，可以设置它来提高 rvs 的性能：

>>> from scipy.stats import norm
>>> rng = SimpleRatioUniforms(dist, mode=0,
...                           pdf_area=np.sqrt(2*np.pi),
...                           cdf_at_mode=norm.cdf(0),
...                           random_state=urng)
>>> rvs = rng.rvs(1000)

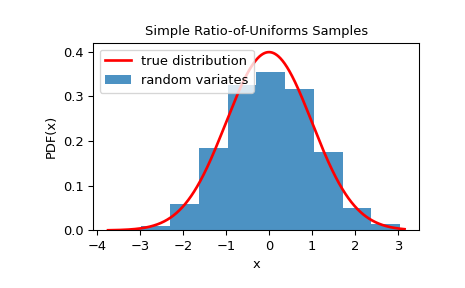
我们可以通过可视化其直方图来检查样本是否来自给定的分布：

>>> import matplotlib.pyplot as plt
>>> x = np.linspace(rvs.min()-0.1, rvs.max()+0.1, 1000)
>>> fx = 1/np.sqrt(2*np.pi) * dist.pdf(x)
>>> fig, ax = plt.subplots()
>>> ax.plot(x, fx, 'r-', lw=2, label='true distribution')
>>> ax.hist(rvs, bins=10, density=True, alpha=0.8, label='random variates')
>>> ax.set_xlabel('x')
>>> ax.set_ylabel('PDF(x)')
>>> ax.set_title('Simple Ratio-of-Uniforms Samples')
>>> ax.legend()
>>> plt.show()
../../_images/scipy-stats-sampling-SimpleRatioUniforms-1.png
On this page