scipy.stats.

theilslopes#

scipy.stats.theilslopes(y, x=None, alpha=0.95, method='separate')[源代码][源代码]#

计算一组点 (x, y) 的 Theil-Sen 估计量。

theilslopes 实现了一种稳健的线性回归方法。它计算斜率为所有配对值之间斜率的中位数。

参数:

yarray_like

因变量。

x类似数组或无，可选

自变量。如果为 None，则使用 arange(len(y)) 代替。

alphafloat, 可选

置信度在 0 到 1 之间。默认是 95% 置信度。注意 alpha 在 0.5 附近是对称的，即 0.1 和 0.9 都被解释为“找到 90% 置信区间”。

方法{‘联合’, ‘分开’}, 可选

用于计算截距估计值的方法。支持以下方法，

‘joint’: 使用 np.median(y - slope * x) 作为截距。

‘separate’: 使用 np.median(y) - 斜率 * np.median(x)
作为拦截。

默认值为 ‘separate’。

Added in version 1.8.0.

返回:

结果 : TheilslopesResult 实例TheilslopesResult 实例

返回值是一个具有以下属性的对象：

斜率浮动: Theil 斜率。
拦截浮动: Theil 线的截距。
低坡度浮动: 置信区间在 slope 上的下限。
陡坡浮动: 置信区间在 slope 上的上限。

参见

siegelslopes: 使用重复中位数的类似技术

注释

theilslopes 的实现遵循 [1]。在 [1] 中未定义截距，此处定义为 median(y) - slope*median(x)，这在 [3] 中给出。文献中存在其他截距定义，例如 [4] 中的 median(y - slope*x)。计算截距的方法可以通过参数 method 确定。由于 [1] 中未涉及此问题，因此未给出截距的置信区间。

为了与旧版本的 SciPy 兼容，返回值的行为类似于长度为 4 的 namedtuple，具有 slope、intercept、low_slope 和 high_slope 字段，因此可以继续编写:

slope, intercept, low_slope, high_slope = theilslopes(y, x)

参考文献

[1] (1,2,3)

P.K. Sen, “基于 Kendall’s tau 的回归系数估计”, J. Am. Stat. Assoc., 第 63 卷, 第 1379-1389 页, 1968 年。

[2]

H. Theil, “A rank-invariant method of linear and polynomial regression analysis I, II and III”, Nederl. Akad. Wetensch., Proc. 53:, pp. 386-392, pp. 521-525, pp. 1397-1412, 1950.

[3]

W.L. Conover, “实用非参数统计”, 第2版, John Wiley and Sons, 纽约, 第493页。

[4]

https://en.wikipedia.org/wiki/Theil%E2%80%93Sen_estimator

示例

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt

>>> x = np.linspace(-5, 5, num=150)
>>> y = x + np.random.normal(size=x.size)
>>> y[11:15] += 10  # add outliers
>>> y[-5:] -= 7

计算斜率、截距和90%的置信区间。为了比较，也使用 linregress 计算最小二乘拟合：

>>> res = stats.theilslopes(y, x, 0.90, method='separate')
>>> lsq_res = stats.linregress(x, y)

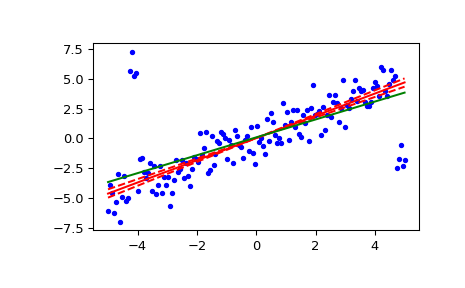
绘制结果。Theil-Sen回归线以红色显示，红色虚线表示斜率的置信区间（注意，红色虚线不是回归的置信区间，因为不包括截距的置信区间）。绿色线显示了用于比较的最小二乘拟合。

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(x, y, 'b.')
>>> ax.plot(x, res[1] + res[0] * x, 'r-')
>>> ax.plot(x, res[1] + res[2] * x, 'r--')
>>> ax.plot(x, res[1] + res[3] * x, 'r--')
>>> ax.plot(x, lsq_res[1] + lsq_res[0] * x, 'g-')
>>> plt.show()

../../_images/scipy-stats-theilslopes-1.png