固定长度模型的困惑度
困惑度(PPL)是评估语言模型最常用的指标之一。在深入探讨之前,我们应该注意到,该指标特别适用于经典语言模型(有时称为自回归或因果语言模型),而对于像BERT这样的掩码语言模型则没有很好的定义(参见模型摘要)。
困惑度被定义为一个序列的指数化平均负对数似然。如果我们有一个标记化的序列,那么的困惑度是,
其中 是第i个标记在前面的标记 条件下的对数似然。直观上,它可以被视为模型在语料库中指定标记集合中均匀预测能力的评估。重要的是,这意味着标记化过程对模型的困惑度有直接影响,在比较不同模型时应始终考虑这一点。
这也等同于数据和模型预测之间的交叉熵的指数化。要了解更多关于困惑度及其与每字符比特数(BPC)和数据压缩的关系的直觉,请查看这个The Gradient上的精彩博客文章。
使用固定长度模型计算PPL
如果我们不受模型上下文大小的限制,我们将通过自回归分解序列并在每一步以整个前序子序列为条件来评估模型的困惑度,如下所示。
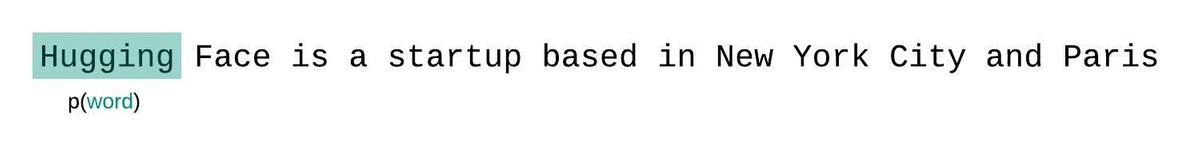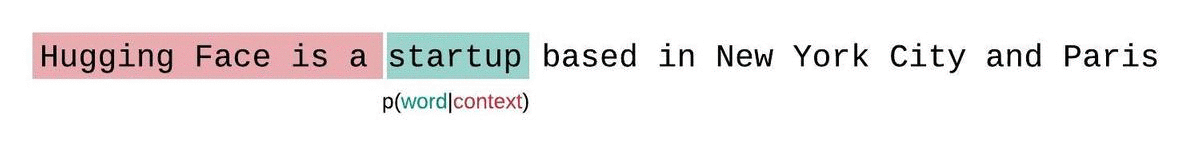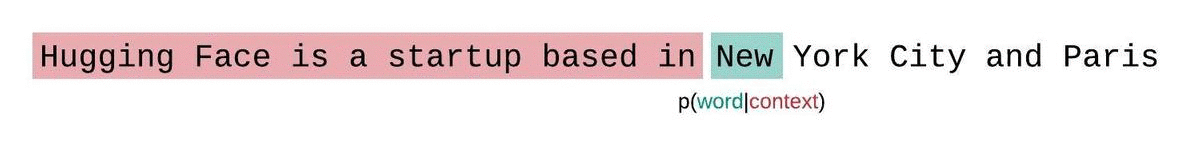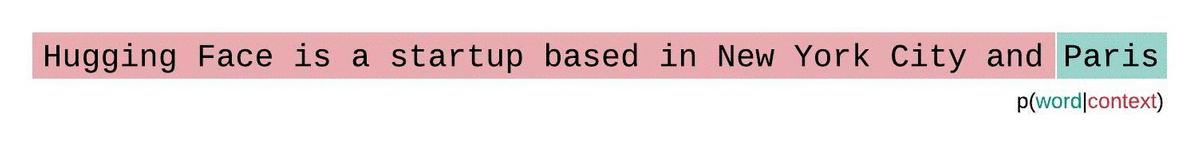
然而,在使用近似模型时,我们通常对模型可以处理的标记数量有限制。例如,GPT-2的最大版本有固定的1024个标记长度,因此当大于1024时,我们不能直接计算。
相反,序列通常被分解为与模型的最大输入大小相等的子序列。如果模型的最大输入大小是,那么我们通过仅以个前导标记为条件来近似标记的可能性,而不是整个上下文。在评估模型对序列的困惑度时,一种诱人但次优的方法是将序列分解为不相交的块,并独立地累加每个段的对数似然。
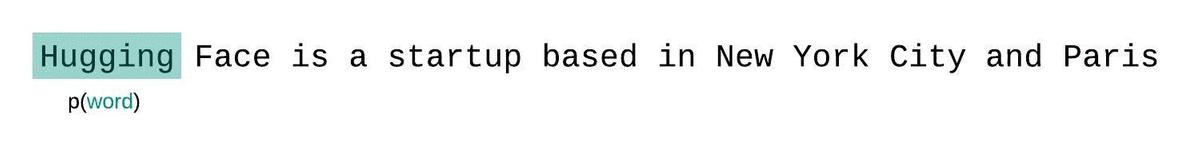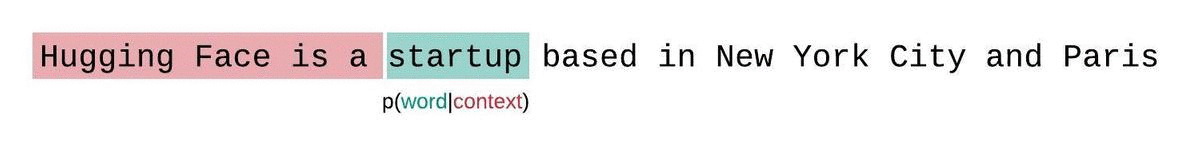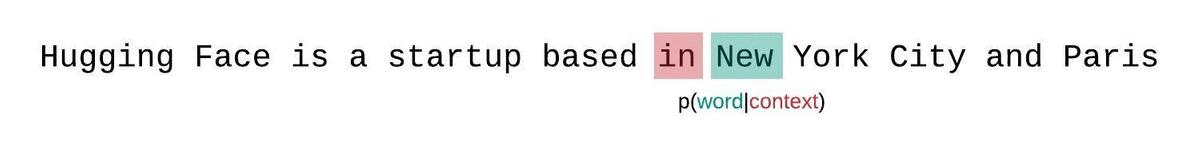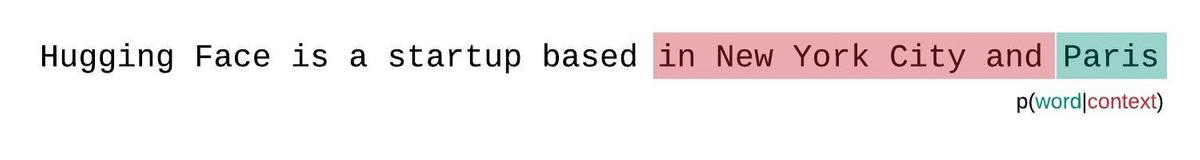
由于每个片段的困惑度可以通过一次前向传递计算出来,因此计算速度很快,但作为完全分解困惑度的近似值效果较差,通常会因为模型在大多数预测步骤中上下文较少而产生更高(更差)的PPL。
相反,固定长度模型的PPL应该使用滑动窗口策略进行评估。这包括重复滑动上下文窗口,以便模型在做出每个预测时有更多的上下文。
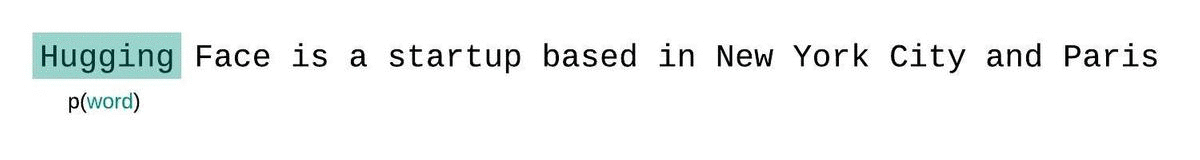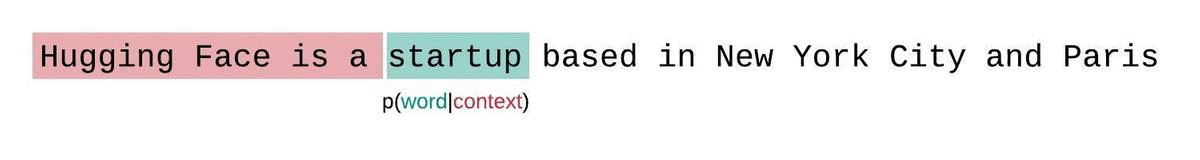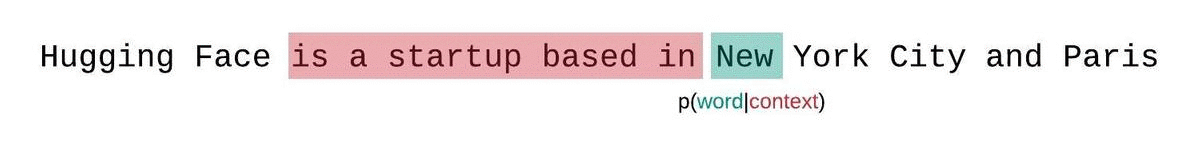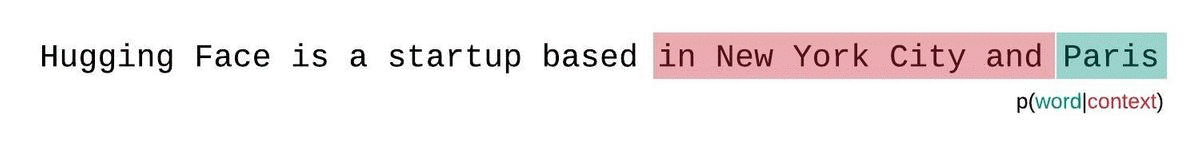
这是对序列概率真实分解的更接近的近似,通常会得到更有利的分数。缺点是它需要对语料库中的每个标记进行单独的前向传递。一个实用的折衷方案是采用跨步滑动窗口,以较大的步幅移动上下文,而不是每次滑动1个标记。这使得计算能够更快地进行,同时仍然为模型提供了在每个步骤进行预测的大上下文。
示例:在🤗 Transformers中使用GPT-2计算困惑度
让我们用GPT-2来演示这个过程。
from transformers import GPT2LMHeadModel, GPT2TokenizerFast
from accelerate.test_utils.testing import get_backend
device, _, _ = get_backend() # automatically detects the underlying device type (CUDA, CPU, XPU, MPS, etc.)
model_id = "openai-community/gpt2-large"
model = GPT2LMHeadModel.from_pretrained(model_id).to(device)
tokenizer = GPT2TokenizerFast.from_pretrained(model_id)我们将加载WikiText-2数据集,并使用几种不同的滑动窗口策略来评估困惑度。由于这个数据集很小,而且我们只对数据集进行一次前向传递,因此我们可以直接将整个数据集加载并编码到内存中。
from datasets import load_dataset
test = load_dataset("wikitext", "wikitext-2-raw-v1", split="test")
encodings = tokenizer("\n\n".join(test["text"]), return_tensors="pt")使用 🤗 Transformers,我们可以简单地将 input_ids 作为 labels 传递给我们的模型,每个标记的平均负对数似然将作为损失返回。然而,使用我们的滑动窗口方法时,每次迭代传递给模型的标记会有重叠。我们不希望仅作为上下文处理的标记的对数似然被包含在损失中,因此我们可以将这些目标设置为 -100,以便忽略它们。以下是一个示例,展示了我们如何使用步长为 512 来实现这一点。这意味着在计算任何一个标记的条件似然时,模型将至少有 512 个标记作为上下文(前提是有 512 个前面的标记可用作条件)。
import torch
from tqdm import tqdm
max_length = model.config.n_positions
stride = 512
seq_len = encodings.input_ids.size(1)
nll_sum = 0.0
n_tokens = 0
prev_end_loc = 0
for begin_loc in tqdm(range(0, seq_len, stride)):
end_loc = min(begin_loc + max_length, seq_len)
trg_len = end_loc - prev_end_loc # may be different from stride on last loop
input_ids = encodings.input_ids[:, begin_loc:end_loc].to(device)
target_ids = input_ids.clone()
target_ids[:, :-trg_len] = -100
with torch.no_grad():
outputs = model(input_ids, labels=target_ids)
# loss is calculated using CrossEntropyLoss which averages over valid labels
# N.B. the model only calculates loss over trg_len - 1 labels, because it internally shifts the labels
# to the left by 1.
neg_log_likelihood = outputs.loss
# Accumulate the total negative log-likelihood and the total number of tokens
num_valid_tokens = (target_ids != -100).sum().item() # number of valid tokens in target_ids
batch_size = target_ids.size(0)
num_loss_tokens = num_valid_tokens - batch_size # subtract batch_size due to internal label shift
nll_sum += neg_log_likelihood * num_loss_tokens
n_tokens += num_loss_tokens
prev_end_loc = end_loc
if end_loc == seq_len:
break
avg_nll = nll_sum / n_tokens # average negative log-likelihood per token
ppl = torch.exp(avg_nll)使用与最大输入长度相等的步幅长度运行此操作等同于我们上面讨论的非最优、非滑动窗口策略。步幅越小,模型在做出每个预测时将拥有更多的上下文,通常报告的困惑度也会更好。
当我们使用stride = 1024运行上述代码时,即没有重叠,得到的PPL为19.44,这与GPT-2论文中报告的19.93大致相同。通过使用stride = 512并采用我们的滑动窗口策略,这个值下降到16.44。这不仅是一个更有利的分数,而且是以更接近序列似然的真正自回归分解的方式计算的。