自动批处理用于贝叶斯推断#
本笔记本演示了一个简单的贝叶斯推断示例,其中自动批处理使用户代码更易于编写、阅读,并且不太可能包含错误。
灵感来自于@davmre的笔记本。
import matplotlib.pyplot as plt
import jax
import jax.numpy as jnp
import jax.scipy as jsp
from jax import random
import numpy as np
import scipy as sp
生成一个虚假的二元分类数据集#
np.random.seed(10009)
num_features = 10
num_points = 100
true_beta = np.random.randn(num_features).astype(jnp.float32)
all_x = np.random.randn(num_points, num_features).astype(jnp.float32)
y = (np.random.rand(num_points) < sp.special.expit(all_x.dot(true_beta))).astype(jnp.int32)
y
array([0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0,
1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0,
1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0,
0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1,
1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0], dtype=int32)
编写模型的对数联合函数#
我们将编写一个非批处理版本,一个手动批处理版本,以及一个自动批处理版本。
非批处理#
def log_joint(beta):
result = 0.
# 请注意,`jnp.sum` 函数未提供 `axis` 参数。
result = result + jnp.sum(jsp.stats.norm.logpdf(beta, loc=0., scale=1.))
result = result + jnp.sum(-jnp.log(1 + jnp.exp(-(2*y-1) * jnp.dot(all_x, beta))))
return result
log_joint(np.random.randn(num_features))
Array(-213.2356, dtype=float32)
# This doesn't work, because we didn't write `log_prob()` to handle batching.
try:
batch_size = 10
batched_test_beta = np.random.randn(batch_size, num_features)
log_joint(np.random.randn(batch_size, num_features))
except ValueError as e:
print("Caught expected exception " + str(e))
Caught expected exception Incompatible shapes for broadcasting: shapes=[(100,), (100, 10)]
手动批处理#
def batched_log_joint(beta):
result = 0.
# 在这里(以及下面),`sum` 需要一个 `axis` 参数。最糟糕的情况是,忘记设置轴。
# 或者设置不当会导致错误;最糟糕的是,它可能会悄然改变
# 模型的语义。
result = result + jnp.sum(jsp.stats.norm.logpdf(beta, loc=0., scale=1.),
axis=-1)
# 注意多次转置。正确处理这个问题并不复杂,
# but it's also not totally mindless. (I didn't get it right on the first
# 尝试。
result = result + jnp.sum(-jnp.log(1 + jnp.exp(-(2*y-1) * jnp.dot(all_x, beta.T).T)),
axis=-1)
return result
batch_size = 10
batched_test_beta = np.random.randn(batch_size, num_features)
batched_log_joint(batched_test_beta)
Array([-147.84033, -207.02205, -109.26076, -243.80833, -163.0291 ,
-143.8485 , -160.28773, -113.7717 , -126.60544, -190.81989], dtype=float32)
自动批处理与 vmap#
它就是这么简单。
vmap_batched_log_joint = jax.vmap(log_joint)
vmap_batched_log_joint(batched_test_beta)
Array([-147.84033, -207.02205, -109.26076, -243.80833, -163.0291 ,
-143.8485 , -160.28773, -113.7717 , -126.60544, -190.81989], dtype=float32)
自包含的变分推断示例#
从上面复制了一些代码。
设置(批处理)日志联合函数#
@jax.jit
def log_joint(beta):
result = 0.
# 注意,`jnp.sum` 没有提供 `axis` 参数。
result = result + jnp.sum(jsp.stats.norm.logpdf(beta, loc=0., scale=10.))
result = result + jnp.sum(-jnp.log(1 + jnp.exp(-(2*y-1) * jnp.dot(all_x, beta))))
return result
batched_log_joint = jax.jit(jax.vmap(log_joint))
定义ELBO及其梯度#
def elbo(beta_loc, beta_log_scale, epsilon):
beta_sample = beta_loc + jnp.exp(beta_log_scale) * epsilon
return jnp.mean(batched_log_joint(beta_sample), 0) + jnp.sum(beta_log_scale - 0.5 * np.log(2*np.pi))
elbo = jax.jit(elbo)
elbo_val_and_grad = jax.jit(jax.value_and_grad(elbo, argnums=(0, 1)))
使用随机梯度下降优化变分下界 (ELBO)#
def normal_sample(key, shape):
"""准状态随机数生成器的便捷函数。"""
new_key, sub_key = random.split(key)
return new_key, random.normal(sub_key, shape)
normal_sample = jax.jit(normal_sample, static_argnums=(1,))
key = random.key(10003)
beta_loc = jnp.zeros(num_features, jnp.float32)
beta_log_scale = jnp.zeros(num_features, jnp.float32)
step_size = 0.01
batch_size = 128
epsilon_shape = (batch_size, num_features)
for i in range(1000):
key, epsilon = normal_sample(key, epsilon_shape)
elbo_val, (beta_loc_grad, beta_log_scale_grad) = elbo_val_and_grad(
beta_loc, beta_log_scale, epsilon)
beta_loc += step_size * beta_loc_grad
beta_log_scale += step_size * beta_log_scale_grad
if i % 10 == 0:
print('{}\t{}'.format(i, elbo_val))
0 -180.8538818359375
10 -113.06045532226562
20 -102.73727416992188
30 -99.787353515625
40 -98.90898132324219
50 -98.29745483398438
60 -98.18633270263672
70 -97.57972717285156
80 -97.28599548339844
90 -97.46996307373047
100 -97.47715759277344
110 -97.5806655883789
120 -97.4943618774414
130 -97.50271606445312
140 -96.86396026611328
150 -97.44197845458984
160 -97.06941223144531
170 -96.84027862548828
180 -97.21337127685547
190 -97.56502532958984
200 -97.26397705078125
210 -97.11979675292969
220 -97.39595794677734
230 -97.16831970214844
240 -97.118408203125
250 -97.24345397949219
260 -97.29788970947266
270 -96.69285583496094
280 -96.96438598632812
290 -97.30055236816406
300 -96.63592529296875
310 -97.03518676757812
320 -97.52909851074219
330 -97.28813171386719
340 -97.07322692871094
350 -97.15620422363281
360 -97.25881958007812
370 -97.19515228271484
380 -97.13092041015625
390 -97.11727905273438
400 -96.938720703125
410 -97.26676940917969
420 -97.35322570800781
430 -97.21007537841797
440 -97.28436279296875
450 -97.16307830810547
460 -97.2612533569336
470 -97.21343231201172
480 -97.23997497558594
490 -97.14913177490234
500 -97.23527526855469
510 -96.93419647216797
520 -97.21209716796875
530 -96.82575988769531
540 -97.01285552978516
550 -96.94176483154297
560 -97.16520690917969
570 -97.2916488647461
580 -97.42941284179688
590 -97.24371337890625
600 -97.15222930908203
610 -97.49844360351562
620 -96.99069213867188
630 -96.88956451416016
640 -96.89968872070312
650 -97.137939453125
660 -97.43706512451172
670 -96.99235534667969
680 -97.15623474121094
690 -97.1869125366211
700 -97.11161041259766
710 -97.78104400634766
720 -97.23226165771484
730 -97.16206359863281
740 -96.99581909179688
750 -96.66722106933594
760 -97.16795349121094
770 -97.51435089111328
780 -97.28900146484375
790 -96.91226196289062
800 -97.17098999023438
810 -97.29048156738281
820 -97.16242218017578
830 -97.1910629272461
840 -97.56382751464844
850 -97.00194549560547
860 -96.86555480957031
870 -96.76338195800781
880 -96.83661651611328
890 -97.12178802490234
900 -97.09554290771484
910 -97.06825256347656
920 -97.11947631835938
930 -96.87930297851562
940 -97.45625305175781
950 -96.69279479980469
960 -97.29376220703125
970 -97.3353042602539
980 -97.34962463378906
990 -97.09675598144531
显示结果#
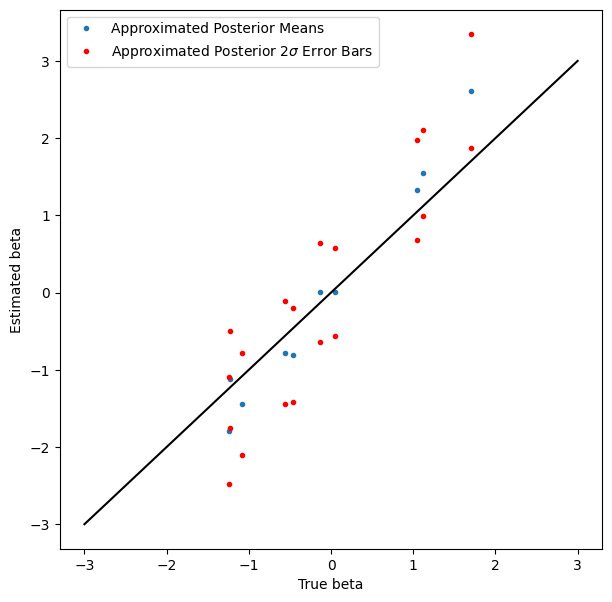
覆盖率虽然不是我们期望的那么好,但也不错,而且没有人说变分推断是精确的。
plt.figure(figsize=(7, 7))
plt.plot(true_beta, beta_loc, '.', label='Approximated Posterior Means')
plt.plot(true_beta, beta_loc + 2*jnp.exp(beta_log_scale), 'r.', label=r'Approximated Posterior $2\sigma$ Error Bars')
plt.plot(true_beta, beta_loc - 2*jnp.exp(beta_log_scale), 'r.')
plot_scale = 3
plt.plot([-plot_scale, plot_scale], [-plot_scale, plot_scale], 'k')
plt.xlabel('True beta')
plt.ylabel('Estimated beta')
plt.legend(loc='best')
<matplotlib.legend.Legend at 0x120e86e50>