make_smoothing_spline#
- scipy.interpolate.make_smoothing_spline(x, y, w=None, lam=None)[源代码][源代码]#
使用
lam计算平滑三次样条函数的(系数),以控制曲线平滑度与数据接近度之间的权衡。如果lam为 None,则使用 GCV 准则 [1] 来确定它。平滑样条作为正则化加权线性回归问题的解被找到:
\[\sum\limits_{i=1}^n w_i\lvert y_i - f(x_i) \rvert^2 + \lambda\int\limits_{x_1}^{x_n} (f^{(2)}(u))^2 d u\]其中,\(f\) 是一个样条函数,\(w\) 是一个权重向量,\(\lambda\) 是一个正则化参数。
如果
lam为 None,我们使用 GCV 准则来找到一个最优的正则化参数,否则我们用给定的参数来解决正则化的加权线性回归问题。该参数控制了以下权衡:参数越大,函数越平滑。- 参数:
- x类数组, 形状 (n,)
横坐标。n 必须至少为 5。
- y类数组, 形状 (n,)
纵坐标。n 必须至少为 5。
- w类似数组,形状 (n,),可选
权重向量。默认是
np.ones_like(x)。- lam : float, (\(\lambda \geq 0\)), 可选float, (\(\lambda \geq 0\)), optional
正则化参数。如果
lam为 None,则根据 GCV 准则找到它。默认为 None。
- 返回:
- 函数一个 BSpline 对象。
一个表示B样条基中的样条的可调用对象,作为使用GCV准则[1]的平滑样条问题的解,如果
lam为None,则使用给定的参数lam。
注释
该算法是对Woltring在FORTRAN中引入的算法的干净房间重新实现 [2]。由于许可证问题,原始版本不能在SciPy源代码中使用。重新实现的细节在这里讨论(仅提供俄文版本) [4]。
如果权重向量
w为 None,我们假设所有点的权重相等,并且权重向量是全一向量。请注意,在加权残差平方和中,权重没有平方:\(\sum\limits_{i=1}^n w_i\lvert y_i - f(x_i) \rvert^2\),而在
splrep中,总和是由平方权重构建的。在初始问题不适定的情况下(例如,产品 \(X^T W X\) 中,其中 \(X\) 是一个设计矩阵,不是一个正定矩阵),会引发 ValueError。
参考文献
[1]G. Wahba, “Estimating the smoothing parameter” in Spline models for observational data, Philadelphia, Pennsylvania: Society for Industrial and Applied Mathematics, 1990, pp. 45-65. DOI:10.1137/1.9781611970128
[2]H. J. Woltring, A Fortran package for generalized, cross-validatory spline smoothing and differentiation, Advances in Engineering Software, vol. 8, no. 2, pp. 104-113, 1986. DOI:10.1016/0141-1195(86)90098-7
[3]T. Hastie, J. Friedman, and R. Tisbshirani, “Smoothing Splines” in The elements of Statistical Learning: Data Mining, Inference, and prediction, New York: Springer, 2017, pp. 241-249. DOI:10.1007/978-0-387-84858-7
[4]E. Zemlyanoy, “Generalized cross-validation smoothing splines”, BSc thesis, 2022. https://www.hse.ru/ba/am/students/diplomas/620910604 (in Russian)
示例
生成一些噪声数据
>>> import numpy as np >>> np.random.seed(1234) >>> n = 200 >>> def func(x): ... return x**3 + x**2 * np.sin(4 * x) >>> x = np.sort(np.random.random_sample(n) * 4 - 2) >>> y = func(x) + np.random.normal(scale=1.5, size=n)
创建一个平滑样条函数
>>> from scipy.interpolate import make_smoothing_spline >>> spl = make_smoothing_spline(x, y)
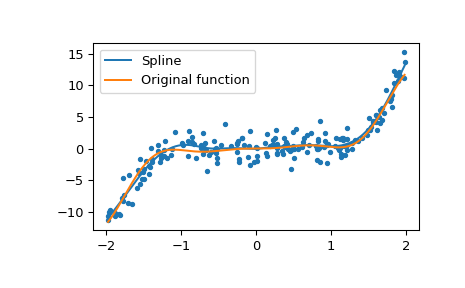
绘制两者
>>> import matplotlib.pyplot as plt >>> grid = np.linspace(x[0], x[-1], 400) >>> plt.plot(grid, spl(grid), label='Spline') >>> plt.plot(grid, func(grid), label='Original function') >>> plt.scatter(x, y, marker='.') >>> plt.legend(loc='best') >>> plt.show()