scipy.interpolate.

make_lsq_spline#

scipy.interpolate.make_lsq_spline(x, y, t, k=3, w=None, axis=0, check_finite=True)[源代码][源代码]#

计算基于 LSQ（最小二乘）拟合的 B 样条的（系数）。

结果是线性组合

\[S(x) = \sum_j c_j B_j(x; t)\]

B样条基元素的 \(B_j(x; t)\)，其最小化

\[\sum_{j} \left( w_j \times (S(x_j) - y_j) \right)^2\]
参数:
xarray_like, 形状 (m,)

横坐标。

y类数组, 形状 (m, …)

纵坐标。

tarray_like, 形状 (n + k + 1,).

结点。结点和数据点必须满足 Schoenberg-Whitney 条件。

kint, 可选

B样条度数。默认是三次，k = 3。

w类数组, 形状 (m,), 可选

样条拟合的权重。必须是正数。如果为 None ，则所有权重相等。默认值为 None 。

轴int, 可选

插值轴。默认值为零。

check_finitebool, 可选

是否检查输入数组是否仅包含有限数字。禁用可能会提高性能，但如果输入包含无穷大或NaN，可能会导致问题（崩溃、非终止）。默认值为True。

返回:
b : 一个次数为 k 且节点为 t 的 BSpline 对象。一个度数为的BSpline对象

参见

BSpline

表示 B 样条对象的基类

make_interp_spline

用于插值样条的类似工厂函数

LSQUnivariateSpline

基于 FITPACK 的样条拟合例程

splrep

基于 FITPACK 的拟合例程

注释

数据点的数量必须大于样条度数 k。

结 t 必须满足 Schoenberg-Whitney 条件，即，必须存在数据点的一个子集 x[j] 使得 t[j] < x[j] < t[j+k+1]，对于 j=0, 1,...,n-k-2。

示例

生成一些噪声数据：

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> x = np.linspace(-3, 3, 50)
>>> y = np.exp(-x**2) + 0.1 * rng.standard_normal(50)

现在拟合一个带有预定义内部节点的平滑三次样条。这里我们通过添加边界节点使节点向量 (k+1) 规则化：

>>> from scipy.interpolate import make_lsq_spline, BSpline
>>> t = [-1, 0, 1]
>>> k = 3
>>> t = np.r_[(x[0],)*(k+1),
...           t,
...           (x[-1],)*(k+1)]
>>> spl = make_lsq_spline(x, y, t, k)

作为对比，我们也为同一组数据构建了一个插值样条：

>>> from scipy.interpolate import make_interp_spline
>>> spl_i = make_interp_spline(x, y)

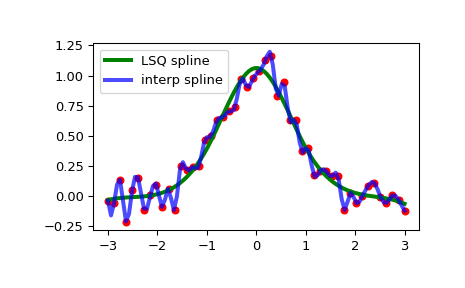
绘制两者：

>>> xs = np.linspace(-3, 3, 100)
>>> plt.plot(x, y, 'ro', ms=5)
>>> plt.plot(xs, spl(xs), 'g-', lw=3, label='LSQ spline')
>>> plt.plot(xs, spl_i(xs), 'b-', lw=3, alpha=0.7, label='interp spline')
>>> plt.legend(loc='best')
>>> plt.show()
../../_images/scipy-interpolate-make_lsq_spline-1_00_00.png

NaN 处理: 如果输入数组包含 nan 值，结果将无用，因为底层样条拟合例程无法处理 nan。一种解决方法是使用零权重表示非数字数据点：

>>> y[8] = np.nan
>>> w = np.isnan(y)
>>> y[w] = 0.
>>> tck = make_lsq_spline(x, y, t, w=~w)

注意需要将 nan 替换为一个数值（只要相应的权重为零，精确值并不重要。）

On this page