scipy.interpolate.

LSQUnivariateSpline

class scipy.interpolate.LSQUnivariateSpline(x, y, t, w=None, bbox=[None, None], k=3, ext=0, check_finite=False)

带有显式内部节点的1-D样条。

拟合一个度数为 k 的样条曲线 y = spl(x) 到提供的 x, y 数据。t 指定样条曲线的内部节点。

参数:

x(N,) 数组类

数据点的输入维度 – 必须递增

y(N,) 数组类

数据点的输入维度

t(M,) 数组类

样条的内部节点。必须按升序排列并且:

bbox[0] < t[0] < ... < t[-1] < bbox[-1]

w(N,) 数组类，可选

样条拟合的权重。必须是正数。如果为 None（默认），则所有权重均为 1。

bbox(2,) 数组类，可选

2-序列指定近似区间的边界。如果为 None（默认），则 bbox = [x[0], x[-1]]。

kint, 可选

平滑样条的阶数。必须满足 1 <= k <= 5。默认是 k = 3，即三次样条。

扩展int 或 str, 可选

控制不在由节点序列定义的区间内的元素的外推模式。

• 如果 ext=0 或 ‘extrapolate’，返回外推值。

• 如果 ext=1 或 ‘zeros’，返回 0

• 如果 ext=2 或 ‘raise’，则引发 ValueError

• 如果 ‘const’ 的 ext=3，返回边界值。

默认值为 0。

check_finitebool, 可选

是否检查输入数组是否仅包含有限数字。禁用可能会提高性能，但如果输入包含无穷大或NaN，则可能会导致问题（崩溃、非终止或无意义的结果）。默认值为False。

方法

__call__(x[, nu, ext])	在位置 x 处评估样条（或其 nu 阶导数）。
antiderivative([n])	构建一个新的样条曲线，表示此样条曲线的反导数。
derivative([n])	构造一个新的样条曲线，表示此样条曲线的导数。
derivatives(x)	返回在点 x 处样条的所有导数。
get_coeffs()	返回样条系数。
get_knots()	返回样条曲线的内部节点位置。
get_residual()	返回样条近似中残差的加权平方和。
integral(a, b)	返回给定两点之间样条的定积分。
roots()	返回样条的零点。
set_smoothing_factor(s)	使用给定的平滑因子 s 和在上次调用中找到的节点继续样条计算。

validate_input

Raises:

ValueError

如果内部节点不满足 Schoenberg-Whitney 条件

参见

UnivariateSpline

一个平滑的单变量样条曲线，用于拟合给定的数据点。

InterpolatedUnivariateSpline

给定一组数据点，进行插值的一元样条。

splrep

一个用于找到1-D曲线的B样条表示的函数

splev

一个用于评估B样条或其导数的函数

sproot

一个用于找到三次B样条根的函数

splint

一个用于计算B样条在两个给定点之间定积分的函数

spalde

一个用于评估B样条所有导数的函数

注释

数据点的数量必须大于样条度数 k。

结点 t 必须满足 Schoenberg-Whitney 条件，即，必须存在数据点的一个子集 x[j] 使得 t[j] < x[j] < t[j+k+1]，对于 j=0, 1,...,n-k-2。

示例

Try it in your browser!

>>> import numpy as np
>>> from scipy.interpolate import LSQUnivariateSpline, UnivariateSpline
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> x = np.linspace(-3, 3, 50)
>>> y = np.exp(-x**2) + 0.1 * rng.standard_normal(50)

拟合一个带有预定义内部节点的平滑样条：

>>> t = [-1, 0, 1]
>>> spl = LSQUnivariateSpline(x, y, t)

>>> xs = np.linspace(-3, 3, 1000)
>>> plt.plot(x, y, 'ro', ms=5)
>>> plt.plot(xs, spl(xs), 'g-', lw=3)
>>> plt.show()

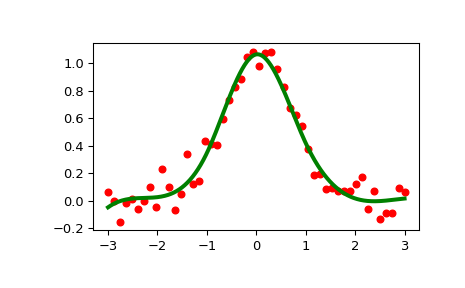
检查节点向量：

>>> spl.get_knots()
array([-3., -1., 0., 1., 3.])

使用另一个样条的节点构建lsq样条：

>>> x = np.arange(10)
>>> s = UnivariateSpline(x, x, s=0)
>>> s.get_knots()
array([ 0.,  2.,  3.,  4.,  5.,  6.,  7.,  9.])
>>> knt = s.get_knots()
>>> s1 = LSQUnivariateSpline(x, x, knt[1:-1])    # Chop 1st and last knot
>>> s1.get_knots()
array([ 0.,  2.,  3.,  4.,  5.,  6.,  7.,  9.])

Go BackOpen In Tab