scipy.linalg.

lstsq#

scipy.linalg.lstsq(a, b, cond=None, overwrite_a=False, overwrite_b=False, check_finite=True, lapack_driver=None)[源代码][源代码]#

计算方程 Ax = b 的最小二乘解。

计算一个向量 x 使得 2-范数 |b - A x| 最小化。

参数:

a(M, N) array_like: 左侧数组
b(M,) 或 (M, K) 数组类: 右侧数组
condfloat, 可选: 用于确定矩阵 a 的有效秩的 ‘小’ 奇异值的截断值。小于 cond * 最大奇异值 的奇异值被视为零。
overwrite_abool, 可选: 丢弃 a 中的数据（可能会提高性能）。默认为 False。
overwrite_bbool, 可选: 丢弃 b 中的数据（可能会提高性能）。默认值为 False。
check_finitebool, 可选: 是否检查输入矩阵是否仅包含有限数值。禁用可能会提高性能，但如果输入包含无穷大或NaN，可能会导致问题（崩溃、无法终止）。
lapack_driverstr, 可选: 用于解决最小二乘问题的LAPACK驱动程序。选项包括 'gelsd'、'gelsy'、'gelss'。默认 ('gelsd') 是一个不错的选择。然而，'gelsy' 在许多问题上可能会稍微快一些。'gelss' 在历史上曾被使用。它通常较慢，但使用更少的内存。

Added in version 0.17.0.

返回:

x(N,) 或 (N, K) ndarray: 最小二乘解。
残基(K,) ndarray 或 float: 如果 M > N 且 rank(A) == n，则返回 b - a x 中每一列的 2-范数的平方（如果 b 是 1-D，则返回标量）。否则返回一个 (0,)-形状的数组。
等级整数: a 的有效秩。
s(min(M, N),) ndarray 或 None: a 的奇异值。a 的条件数是 s[0] / s[-1]。

Raises:

LinAlgError: 如果计算不收敛。
ValueError: 当参数不兼容时。

参见

scipy.optimize.nnls: 非负约束的线性最小二乘法

注释

当 'gelsy' 被用作驱动程序时，residues 被设置为一个 (0,)-形状的数组，而 s 总是 None。

示例

>>> import numpy as np
>>> from scipy.linalg import lstsq
>>> import matplotlib.pyplot as plt

假设我们有以下数据：

>>> x = np.array([1, 2.5, 3.5, 4, 5, 7, 8.5])
>>> y = np.array([0.3, 1.1, 1.5, 2.0, 3.2, 6.6, 8.6])

我们希望将形式为 y = a + b*x**2 的二次多项式拟合到这些数据中。我们首先形成“设计矩阵” M，其中包含一个常数列 1 和一列包含 x**2：

>>> M = x[:, np.newaxis]**[0, 2]
>>> M
array([[  1.  ,   1.  ],
       [  1.  ,   6.25],
       [  1.  ,  12.25],
       [  1.  ,  16.  ],
       [  1.  ,  25.  ],
       [  1.  ,  49.  ],
       [  1.  ,  72.25]])

我们希望找到 M.dot(p) = y 的最小二乘解，其中 p 是一个长度为2的向量，包含参数 a 和 b。

>>> p, res, rnk, s = lstsq(M, y)
>>> p
array([ 0.20925829,  0.12013861])

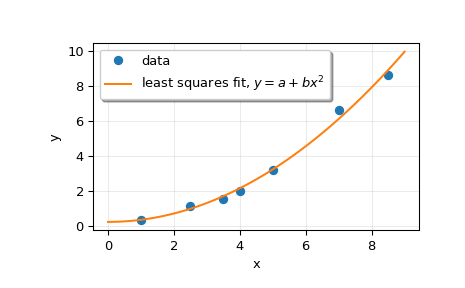
绘制数据和拟合曲线。

>>> plt.plot(x, y, 'o', label='data')
>>> xx = np.linspace(0, 9, 101)
>>> yy = p[0] + p[1]*xx**2
>>> plt.plot(xx, yy, label='least squares fit, $y = a + bx^2$')
>>> plt.xlabel('x')
>>> plt.ylabel('y')
>>> plt.legend(framealpha=1, shadow=True)
>>> plt.grid(alpha=0.25)
>>> plt.show()