curve_fit#
- scipy.optimize.curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False, check_finite=None, bounds=(-inf, inf), method=None, jac=None, *, full_output=False, nan_policy=None, **kwargs)[源代码][源代码]#
使用非线性最小二乘法来拟合一个函数 f 到数据上。
假设
ydata = f(xdata, *params) + eps。- 参数:
- f可调用
模型函数,f(x, …)。它必须将自变量作为第一个参数,并将拟合参数作为剩余的单独参数。
- xdataarray_like
测量数据的独立变量。通常应为 M 长度的序列或具有 k 个预测变量的函数的 (k,M) 形状的数组,如果它是类似数组的对象,则每个元素应可转换为浮点数。
- ydataarray_like
依赖数据,一个长度为 M 的数组 - 名义上是
f(xdata, ...)。- p0类似数组, 可选
参数的初始猜测值(长度为 N)。如果为 None,则初始值将全部为 1(如果可以通过内省确定函数的参数数量,否则将引发 ValueError)。
- sigmaNone 或标量或 M 长度的序列或 MxM 数组,可选
确定 ydata 中的不确定性。如果我们定义残差为
r = ydata - f(xdata, *popt),那么 sigma 的解释取决于其维数:标量或一维 sigma 应包含 ydata 中误差的标准偏差值。在这种情况下,优化的函数是
chisq = sum((r / sigma) ** 2)。二维的 sigma 应包含 ydata 中误差的协方差矩阵。在这种情况下,优化的函数是
chisq = r.T @ inv(sigma) @ r。Added in version 0.19.
None(默认)等同于用1填充的1-D sigma。
- absolute_sigmabool, 可选
如果为 True,sigma 以绝对值使用,并且估计的参数协方差 pcov 反映这些绝对值。
如果为 False(默认),则只有 sigma 值的相对大小重要。返回的参数协方差矩阵 pcov 是基于将 sigma 按一个常数因子缩放的结果。这个常数是通过要求在使用 缩放后 的 sigma 时,最优参数 popt 的减少 chisq 等于一来设定的。换句话说,sigma 被缩放以匹配拟合后残差的样本方差。默认是 False。在数学上,
pcov(absolute_sigma=False) = pcov(absolute_sigma=True) * chisq(popt)/(M-N)- check_finitebool, 可选
如果为 True,检查输入数组是否不包含 nans 或 infs,如果包含则引发 ValueError。将此参数设置为 False 可能会在输入数组包含 nans 时静默地产生无意义的结果。默认情况下,如果未明确指定 nan_policy,则为 True,否则为 False。
- bounds : 数组类或
Bounds的 2-tuple,可选数组类对象的2元组或 参数的下限和上限。默认为无界限。有两种方式指定界限:
Bounds类的实例。2-tuple of array_like: 元组的每个元素必须是长度等于参数数量的数组,或者是标量(在这种情况下,边界对所有参数都相同)。使用
np.inf并带有适当的符号来禁用所有或某些参数的边界。
- 方法{‘lm’, ‘trf’, ‘dogbox’}, 可选
用于优化的方法。有关更多详细信息,请参阅
least_squares。默认值为 ‘lm’ 用于无约束问题,如果提供了 bounds,则为 ‘trf’。当观测数量少于变量数量时,方法 ‘lm’ 将无法工作,此时请使用 ‘trf’ 或 ‘dogbox’。Added in version 0.17.
- jac可调用对象、字符串或 None,可选
具有签名
jac(x, ...)的函数,用于计算模型函数相对于参数的雅可比矩阵,作为类似数组的密集结构。它将根据提供的 sigma 进行缩放。如果为 None(默认),则将通过数值方法估计雅可比矩阵。对于 ‘trf’ 和 ‘dogbox’ 方法,可以使用字符串关键字来选择有限差分方案,参见least_squares。Added in version 0.18.
- 完整输出布尔值,可选
如果为真,此函数返回附加信息:infodict、mesg 和 ier。
Added in version 1.9.
- nan_policy{‘raise’, ‘omit’, None}, 可选
定义当输入包含 nan 时如何处理。以下选项可用(默认是 None):
‘raise’: 抛出一个错误
‘omit’: 执行计算时忽略 nan 值
None: 不执行对 NaN 的特殊处理(除了 check_finite 所做的处理);当存在 NaN 时,行为取决于实现,并且可能会改变。
请注意,如果此值被显式指定(不为 None),check_finite 将被设置为 False。
Added in version 1.11.
- **kwargs
传递给
leastsq的关键字参数用于method='lm',或者传递给least_squares的其他情况。
- 返回:
- popt数组
参数的最佳值,使得
f(xdata, *popt) - ydata的残差平方和最小化。- pcov二维数组
popt 的估计近似协方差。对角线提供了参数估计的方差。要计算参数的一个标准差误差,请使用
perr = np.sqrt(np.diag(pcov))。请注意,cov 和参数误差估计之间的关系是基于模型函数在最佳值附近线性近似的推导 [1]。当这种近似变得不准确时,cov 可能无法提供准确的不确定性度量。sigma 参数如何影响估计的协方差取决于 absolute_sigma 参数,如上所述。
如果在解处的雅可比矩阵没有满秩,那么 ‘lm’ 方法返回一个填充了
np.inf的矩阵,另一方面,’trf’ 和 ‘dogbox’ 方法使用 Moore-Penrose 伪逆来计算协方差矩阵。条件数较大的协方差矩阵(例如使用numpy.linalg.cond计算的)可能表明结果不可靠。- infodict : dict (仅在 full_output 为 True 时返回)dict(仅在返回时)
一个带有键的可选输出字典:
nfev函数调用的次数。方法 ‘trf’ 和 ‘dogbox’ 不计算数值雅可比近似的函数调用次数,这与 ‘lm’ 方法不同。
fvec在解处评估的残差值,对于一维 sigma 来说,这是
(f(x, *popt) - ydata)/sigma。fjacQR 分解的最终近似雅可比矩阵的 R 矩阵的排列,按列存储。与 ipvt 一起,可以近似估计的协方差。方法 ‘lm’ 仅提供此信息。
ipvt一个长度为 N 的整数数组,定义了一个置换矩阵 p,使得 fjac*p = q*r,其中 r 是上三角矩阵,其对角元素的幅度非递增。p 的第 j 列是单位矩阵的第 ipvt(j) 列。方法 ‘lm’ 仅提供此信息。
qtf向量 (转置(q) * fvec)。方法 ‘lm’ 仅提供此信息。
Added in version 1.9.
- mesg : str (仅在 full_output 为 True 时返回)str (仅在返回时)
提供关于解决方案的信息的字符串消息。
Added in version 1.9.
- ier : int (仅在 full_output 为 True 时返回)int (仅在返回时)
一个整数标志。如果它等于1、2、3或4,则找到了解决方案。否则,未找到解决方案。在任何情况下,可选的输出变量 mesg 提供更多信息。
Added in version 1.9.
- Raises:
- ValueError
如果 ydata 或 xdata 包含 NaN,或者使用了不兼容的选项。
- RuntimeError
如果最小二乘最小化失败。
- OptimizeWarning
如果无法估计参数的协方差。
参见
least_squares最小化非线性函数平方和。
scipy.stats.linregress计算两组测量值的线性最小二乘回归。
注释
用户应确保输入 xdata、ydata 以及 f 的输出为
float64,否则优化可能会返回不正确的结果。使用
method='lm'时,算法通过leastsq使用 Levenberg-Marquardt 算法。请注意,此算法只能处理无约束问题。箱型约束可以通过方法 ‘trf’ 和 ‘dogbox’ 来处理。更多信息请参阅
least_squares的文档字符串。需要拟合的参数必须具有相似的尺度。数量级差异过大可能导致不正确的结果。对于 ‘trf’ 和 ‘dogbox’ 方法,可以使用 x_scale 关键字参数来缩放参数。
参考文献
- [1] K. Vugrin 等人。非线性置信区域估计技术
地下水流动的回归分析:三个案例研究。水资源研究,第43卷,W03423,DOI:10.1029/2005WR004804
示例
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.optimize import curve_fit
>>> def func(x, a, b, c): ... return a * np.exp(-b * x) + c
定义带有噪声的拟合数据:
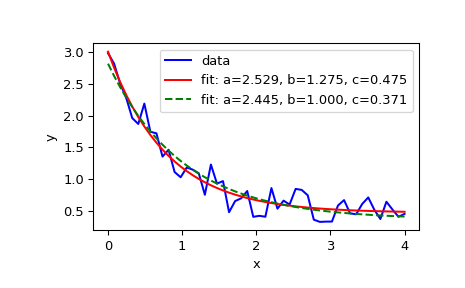
>>> xdata = np.linspace(0, 4, 50) >>> y = func(xdata, 2.5, 1.3, 0.5) >>> rng = np.random.default_rng() >>> y_noise = 0.2 * rng.normal(size=xdata.size) >>> ydata = y + y_noise >>> plt.plot(xdata, ydata, 'b-', label='data')
适用于函数 func 的参数 a, b, c:
>>> popt, pcov = curve_fit(func, xdata, ydata) >>> popt array([2.56274217, 1.37268521, 0.47427475]) >>> plt.plot(xdata, func(xdata, *popt), 'r-', ... label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))
将优化限制在
0 <= a <= 3,0 <= b <= 1和0 <= c <= 0.5的区域内:>>> popt, pcov = curve_fit(func, xdata, ydata, bounds=(0, [3., 1., 0.5])) >>> popt array([2.43736712, 1. , 0.34463856]) >>> plt.plot(xdata, func(xdata, *popt), 'g--', ... label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))
>>> plt.xlabel('x') >>> plt.ylabel('y') >>> plt.legend() >>> plt.show()
为了获得可靠的结果,模型 func 不应过度参数化;冗余参数可能导致协方差矩阵不可靠,并且在某些情况下,可能导致拟合质量下降。作为快速检查模型是否可能过度参数化的方法,计算协方差矩阵的条件数:
>>> np.linalg.cond(pcov) 34.571092161547405 # may vary
这个值很小,所以不会引起太多关注。然而,如果我们向 func 添加第四个参数
d,其效果与a相同:>>> def func2(x, a, b, c, d): ... return a * d * np.exp(-b * x) + c # a and d are redundant >>> popt, pcov = curve_fit(func2, xdata, ydata) >>> np.linalg.cond(pcov) 1.13250718925596e+32 # may vary
如此大的值值得关注。协方差矩阵的对角元素,与拟合的不确定性相关,提供了更多信息:
>>> np.diag(pcov) array([1.48814742e+29, 3.78596560e-02, 5.39253738e-03, 2.76417220e+28]) # may vary
注意,第一个和最后一个项比其他元素大得多,这表明这些参数的最优值是不明确的,并且模型中只需要其中一个参数。
如果 f 的最优参数相差多个数量级,那么得到的结果可能不准确。有时,
curve_fit可能无法找到任何结果:>>> ydata = func(xdata, 500000, 0.01, 15) >>> try: ... popt, pcov = curve_fit(func, xdata, ydata, method = 'trf') ... except RuntimeError as e: ... print(e) Optimal parameters not found: The maximum number of function evaluations is exceeded.
如果参数比例大致已知,可以在 x_scale 参数中定义:
>>> popt, pcov = curve_fit(func, xdata, ydata, method = 'trf', ... x_scale = [1000, 1, 1]) >>> popt array([5.00000000e+05, 1.00000000e-02, 1.49999999e+01])