scipy.special.huber#
- scipy.special.huber(delta, r, out=None) = <ufunc 'huber'>#
Huber 损失函数。
\[\begin{split}\text{huber}(\delta, r) = \begin{cases} \infty & \delta < 0 \\ \frac{1}{2}r^2 & 0 \le \delta, | r | \le \delta \\ \delta ( |r| - \frac{1}{2}\delta ) & \text{否则} \end{cases}\end{split}\]- 参数:
- deltandarray
输入数组,指示二次与线性损失的变化点。
- rndarray
输入数组,可能表示残差。
- 出ndarray,可选
函数值的可选输出数组
- 返回:
- 标量或ndarray
计算出的Huber损失函数值。
参见
pseudo_huber此函数的平滑近似
注释
huber在稳健统计或机器学习中作为损失函数时非常有用,与常见的平方误差损失相比,它可以减少异常值的影响,幅度大于 delta 的残差不会被平方 [1]。通常,r 表示残差,即模型预测与数据之间的差异。然后,对于 \(|r|\leq\delta\),
huber类似于平方误差,而对于 \(|r|>\delta\),它类似于绝对误差。这样,Huber 损失通常在模型拟合中对小残差(如平方误差损失函数)实现快速收敛,同时仍然减少异常值(\(|r|>\delta\))的影响(如绝对误差损失)。由于 \(\delta\) 是平方误差和绝对误差之间的分界点,因此需要针对每个问题仔细调整。huber也是凸的,使其适用于基于梯度的优化。Added in version 0.15.0.
参考文献
[1]Peter Huber. “位置参数的稳健估计”, 1964. 统计年鉴. 53 (1): 73 - 101.
示例
导入所有必要的模块。
>>> import numpy as np >>> from scipy.special import huber >>> import matplotlib.pyplot as plt
计算
delta=1在r=2处的函数>>> huber(1., 2.) 1.5
通过为 delta 提供一个 NumPy 数组或列表来计算不同 delta 的函数。
>>> huber([1., 3., 5.], 4.) array([3.5, 7.5, 8. ])
通过为 r 提供一个 NumPy 数组或列表,在不同的点上计算函数。
>>> huber(2., np.array([1., 1.5, 3.])) array([0.5 , 1.125, 4. ])
通过为 delta 和 r 提供兼容广播形状的数组,可以计算不同 delta 和 r 的函数。
>>> r = np.array([1., 2.5, 8., 10.]) >>> deltas = np.array([[1.], [5.], [9.]]) >>> print(r.shape, deltas.shape) (4,) (3, 1)
>>> huber(deltas, r) array([[ 0.5 , 2. , 7.5 , 9.5 ], [ 0.5 , 3.125, 27.5 , 37.5 ], [ 0.5 , 3.125, 32. , 49.5 ]])
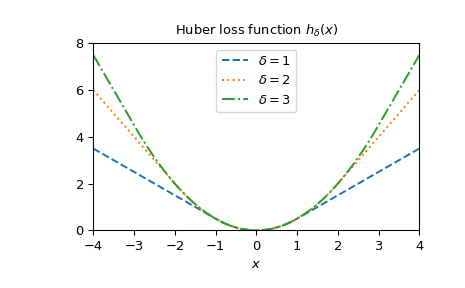
绘制不同 delta 的函数。
>>> x = np.linspace(-4, 4, 500) >>> deltas = [1, 2, 3] >>> linestyles = ["dashed", "dotted", "dashdot"] >>> fig, ax = plt.subplots() >>> combined_plot_parameters = list(zip(deltas, linestyles)) >>> for delta, style in combined_plot_parameters: ... ax.plot(x, huber(delta, x), label=fr"$\delta={delta}$", ls=style) >>> ax.legend(loc="upper center") >>> ax.set_xlabel("$x$") >>> ax.set_title(r"Huber loss function $h_{\delta}(x)$") >>> ax.set_xlim(-4, 4) >>> ax.set_ylim(0, 8) >>> plt.show()