scipy.special.smirnov

scipy.special.smirnov(n, d, out=None) = <ufunc 'smirnov'>

Kolmogorov-Smirnov 互补累积分布函数

返回Kolmogorov-Smirnov互补累积分布函数（即生存函数）的精确值，用于检验基于`n`样本的经验分布与理论分布之间相等性的一侧检验。它等于基于`n`样本的理论分布与经验分布之间的最大差异大于d的概率。

参数:

n整数

样本数量

d浮点数 类数组

经验累积分布函数 (ECDF) 与目标累积分布函数之间的偏差。

出ndarray，可选

函数结果的可选输出数组

返回:

标量或ndarray

smirnov(n, d) 的值，Prob(Dn+ >= d) (同样 Prob(Dn- >= d))

参见

smirnovi

分布的逆生存函数

scipy.stats.ksone

提供作为连续分布的功能

kolmogorov, kolmogi

双边分布的函数

注释

smirnov 在应用 Kolmogorov-Smirnov 拟合优度检验时被 stats.kstest 使用。出于历史原因，此函数在 scpy.special 中暴露，但推荐使用 stats.ksone 分布来实现最准确的 CDF/SF/PDF/PPF/ISF 计算。

示例

Try it in your browser!

>>> import numpy as np
>>> from scipy.special import smirnov
>>> from scipy.stats import norm

显示样本大小为5时，间隙至少为0、0.5和1.0的概率。

>>> smirnov(5, [0, 0.5, 1.0])
array([ 1.   ,  0.056,  0.   ])

将大小为5的样本与N(0, 1)进行比较，N(0, 1)是均值为0、标准差为1的标准正态分布。

x 是样本。

>>> x = np.array([-1.392, -0.135, 0.114, 0.190, 1.82])

>>> target = norm(0, 1)
>>> cdfs = target.cdf(x)
>>> cdfs
array([0.0819612 , 0.44630594, 0.5453811 , 0.57534543, 0.9656205 ])

构建经验累积分布函数和K-S统计量（Dn+，Dn-，Dn）。

>>> n = len(x)
>>> ecdfs = np.arange(n+1, dtype=float)/n
>>> cols = np.column_stack([x, ecdfs[1:], cdfs, cdfs - ecdfs[:n],
...                        ecdfs[1:] - cdfs])
>>> with np.printoptions(precision=3):
...    print(cols)
[[-1.392  0.2    0.082  0.082  0.118]
 [-0.135  0.4    0.446  0.246 -0.046]
 [ 0.114  0.6    0.545  0.145  0.055]
 [ 0.19   0.8    0.575 -0.025  0.225]
 [ 1.82   1.     0.966  0.166  0.034]]
>>> gaps = cols[:, -2:]
>>> Dnpm = np.max(gaps, axis=0)
>>> print(f'Dn-={Dnpm[0]:f}, Dn+={Dnpm[1]:f}')
Dn-=0.246306, Dn+=0.224655
>>> probs = smirnov(n, Dnpm)
>>> print(f'For a sample of size {n} drawn from N(0, 1):',
...       f' Smirnov n={n}: Prob(Dn- >= {Dnpm[0]:f}) = {probs[0]:.4f}',
...       f' Smirnov n={n}: Prob(Dn+ >= {Dnpm[1]:f}) = {probs[1]:.4f}',
...       sep='\n')
For a sample of size 5 drawn from N(0, 1):
 Smirnov n=5: Prob(Dn- >= 0.246306) = 0.4711
 Smirnov n=5: Prob(Dn+ >= 0.224655) = 0.5245

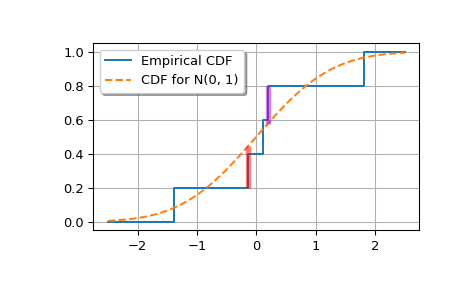
绘制经验累积分布函数和标准正态累积分布函数。

>>> import matplotlib.pyplot as plt
>>> plt.step(np.concatenate(([-2.5], x, [2.5])),
...          np.concatenate((ecdfs, [1])),
...          where='post', label='Empirical CDF')
>>> xx = np.linspace(-2.5, 2.5, 100)
>>> plt.plot(xx, target.cdf(xx), '--', label='CDF for N(0, 1)')

添加标记 Dn+ 和 Dn- 的垂直线。

>>> iminus, iplus = np.argmax(gaps, axis=0)
>>> plt.vlines([x[iminus]], ecdfs[iminus], cdfs[iminus], color='r',
...            alpha=0.5, lw=4)
>>> plt.vlines([x[iplus]], cdfs[iplus], ecdfs[iplus+1], color='m',
...            alpha=0.5, lw=4)

>>> plt.grid(True)
>>> plt.legend(framealpha=1, shadow=True)
>>> plt.show()

Go BackOpen In Tab