scipy.special.struve#
- scipy.special.struve(v, x, out=None) = <ufunc 'struve'>#
Struve 函数。
返回阶数 v 在 x 处的 Struve 函数的值。Struve 函数定义为,
\[ \begin{align}\begin{aligned}H_v(x) = (z/2)^{v + 1} \sum_{n=0}^\infty \frac{(-1)^n (z/2)^{2n}}{\Gamma(n + \frac{3}{2}) \Gamma(n + v + \frac{3}{2})},\\H_v(x) = (z/2)^{v + 1} \sum_{n=0}^\infty \frac{(-1)^n (z/2)^{2n}}{\Gamma(n + \frac{3}{2}) \Gamma(n + v + \frac{3}{2})},\end{aligned}\end{align} \]其中 \(\Gamma\) 是伽马函数。
- 参数:
- varray_like
Struve 函数的阶数(浮点数)。
- xarray_like
Struve 函数的参数(浮点数;除非 v 是整数,否则必须为正)。
- 出ndarray,可选
函数结果的可选输出数组
- 返回:
- H标量或ndarray
Struve 函数在阶数 v 处 x 的值。
参见
modstruve修正 Struve 函数
注释
在 [1] 中讨论的三种方法用于评估 Struve 函数:
幂级数
贝塞尔函数中的展开(如果 \(|z| < |v| + 20\))
渐近大z展开(如果 \(z \geq 0.7v + 12\))
根据和中的最大项估计舍入误差,并返回与最小误差相关的结果。
参考文献
[1]NIST 数学函数数字图书馆 https://dlmf.nist.gov/11
示例
计算阶数为1的Struve函数在2处的值。
>>> import numpy as np >>> from scipy.special import struve >>> import matplotlib.pyplot as plt >>> struve(1, 2.) 0.6467637282835622
计算在2处的Struve函数,阶数为1、2和3,通过为阶数参数`v`提供一个列表。
>>> struve([1, 2, 3], 2.) array([0.64676373, 0.28031806, 0.08363767])
通过为 x 提供一个数组,计算阶数为 1 的 Struve 函数在多个点的值。
>>> points = np.array([2., 5., 8.]) >>> struve(1, points) array([0.64676373, 0.80781195, 0.48811605])
通过为 v 和 z 提供数组,计算多个阶数在多个点的 Struve 函数。数组必须能够广播到正确的形状。
>>> orders = np.array([[1], [2], [3]]) >>> points.shape, orders.shape ((3,), (3, 1))
>>> struve(orders, points) array([[0.64676373, 0.80781195, 0.48811605], [0.28031806, 1.56937455, 1.51769363], [0.08363767, 1.50872065, 2.98697513]])
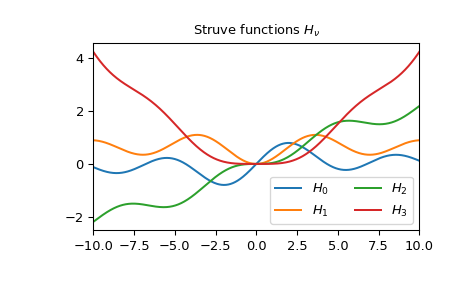
绘制从 -10 到 10 的 0 到 3 阶 Struve 函数。
>>> fig, ax = plt.subplots() >>> x = np.linspace(-10., 10., 1000) >>> for i in range(4): ... ax.plot(x, struve(i, x), label=f'$H_{i!r}$') >>> ax.legend(ncol=2) >>> ax.set_xlim(-10, 10) >>> ax.set_title(r"Struve functions $H_{\nu}$") >>> plt.show()