scipy.stats.

boxcox_normmax

scipy.stats.boxcox_normmax(x, brack=None, method='pearsonr', optimizer=None, *, ymax=BIG_FLOAT)

计算输入数据的最优 Box-Cox 变换参数。

参数:

xarray_like

输入数组。所有条目必须是正的、有限的、实数。

括号2-元组，可选，默认值为 (-2.0, 2.0)

默认 optimize.brent 求解器的下坡括号搜索的起始区间。请注意，在大多数情况下，这并不关键；最终结果允许超出此括号范围。如果传递了 optimizer，则 brack 必须为 None。

方法str, 可选

确定最优变换参数（boxcox lmbda 参数）的方法。选项有：

‘pearsonr’ (默认)

最大化 y = boxcox(x) 与 x 如果呈正态分布时 y 的期望值之间的皮尔逊相关系数。

‘mle’

最大化对数似然 boxcox_llf。这是在 boxcox 中使用的方法。

‘全部’

使用所有可用的优化方法，并返回所有结果。有助于比较不同的方法。

优化器, 可选可调用，可选

optimizer 是一个接受一个参数的可调用对象：

乐趣可调用

要最小化的目标函数。fun 接受一个参数，即 Box-Cox 变换参数 lmbda，并返回在给定参数下的函数值（例如，负对数似然）。optimizer 的工作是找到使 fun 最小化 的 lmbda 值。

并返回一个对象，例如 scipy.optimize.OptimizeResult 的实例，该对象在属性 x 中保存了 lmbda 的最优值。

请参见下面的示例或 scipy.optimize.minimize_scalar 的文档以获取更多信息。

ymaxfloat, 可选

无约束的最优变换参数可能导致Box-Cox变换后的数据具有极端大小，甚至溢出。此参数约束MLE优化，使得变换后的`x`的大小不超过`ymax`。默认值为输入数据类型的最大值。如果设置为无穷大，`boxcox_normmax`返回无约束的最优lambda。当``method=’pearsonr’``时忽略。

返回:

maxlog浮点数或ndarray

找到的最优变换参数。对于 method='all'，这是一个数组而不是标量。

参见

boxcox, boxcox_llf, boxcox_normplot, scipy.optimize.minimize_scalar

示例

Try it in your browser!

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt

我们可以生成一些数据，并通过多种方式确定最佳的 lmbda：

>>> rng = np.random.default_rng()
>>> x = stats.loggamma.rvs(5, size=30, random_state=rng) + 5
>>> y, lmax_mle = stats.boxcox(x)
>>> lmax_pearsonr = stats.boxcox_normmax(x)

>>> lmax_mle
2.217563431465757
>>> lmax_pearsonr
2.238318660200961
>>> stats.boxcox_normmax(x, method='all')
array([2.23831866, 2.21756343])

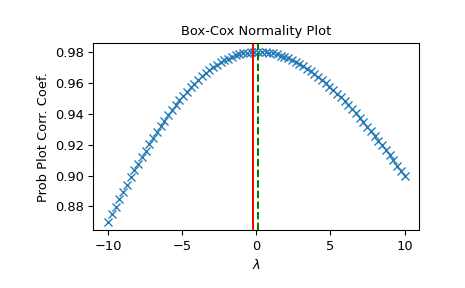
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> prob = stats.boxcox_normplot(x, -10, 10, plot=ax)
>>> ax.axvline(lmax_mle, color='r')
>>> ax.axvline(lmax_pearsonr, color='g', ls='--')

>>> plt.show()

或者，我们可以定义自己的 optimizer 函数。假设我们只对区间 [6, 7] 上的 lmbda 值感兴趣，我们希望使用 scipy.optimize.minimize_scalar 并设置 method='bounded'，并且在优化对数似然函数时使用更严格的容差。为此，我们定义一个接受位置参数 fun 的函数，并使用 scipy.optimize.minimize_scalar 在提供的边界和容差条件下最小化 fun：

>>> from scipy import optimize
>>> options = {'xatol': 1e-12}  # absolute tolerance on `x`
>>> def optimizer(fun):
...     return optimize.minimize_scalar(fun, bounds=(6, 7),
...                                     method="bounded", options=options)
>>> stats.boxcox_normmax(x, optimizer=optimizer)
6.000000000

Go BackOpen In Tab