scipy.stats.

力量

scipy.stats.power(test, rvs, n_observations, *, significance=0.01, vectorized=None, n_resamples=10000, batch=None, kwargs=None)

在备择假设下模拟假设检验的效力。

参数:

测试可调用

要模拟功效的假设检验。test 必须是一个可调用对象，接受一个样本（例如 test(sample)）或 len(rvs) 个单独的样本（例如，如果 rvs 包含两个可调用对象且 n_observations 包含两个值，则为 test(samples1, sample2)）并返回检验的 p 值。如果 vectorized 设置为 True，test 还必须接受一个关键字参数 axis，并且是向量化的，以便沿着提供的样本 axis 执行检验。scipy.stats 中任何带有 axis 参数并返回具有 pvalue 属性的对象的可调用对象也是可以接受的。

rvs可调用对象或可调用对象的元组

一个可调用对象或多个可调用对象的序列，用于在备择假设下生成随机变量。rvs 的每个元素必须接受关键字参数 size``（例如 ``rvs(size=(m, n))）并返回该形状的 N 维数组。如果 rvs 是一个序列，rvs 中的可调用对象数量必须与 n_observations 的元素数量匹配，即 len(rvs) == len(n_observations)。如果 rvs 是一个单独的可调用对象，n_observations 被视为单个元素。

n_observationsints 的元组或整数数组的元组

如果是一个整数序列，每个整数表示要传递给 test 的样本大小。如果是一个整数数组的序列，则对每组相应的样本大小进行功率模拟。参见示例。

重要性浮点数或浮点数数组，默认值：0.01

显著性的阈值；即，p值低于此值时，假设检验结果将被视为反对零假设的证据。等效地，在零假设下可接受的I类错误率。如果是一个数组，则针对每个显著性阈值模拟功效。

kwargsdict, 可选

传递给 rvs 和/或 test 可调用对象的关键字参数。使用内省来确定可以传递给每个可调用对象的关键字参数。每个关键字对应的值必须是一个数组。数组必须能够相互广播，并且能够与 n_observations 中的每个数组广播。对于每组相应的样本大小和参数，模拟计算其功效。参见示例。

矢量化bool, 可选

如果 vectorized 设置为 False，test 将不会传递关键字参数 axis，并且预期仅对 1D 样本执行测试。如果为 True，test 将传递关键字参数 axis，并且预期在传递 N-D 样本数组时沿 axis 执行测试。如果为 None``（默认），如果 `test` 的参数中包含 `axis`，则 `vectorized` 将被设置为 ``True。使用向量化测试通常会减少计算时间。

n_resamplesint, 默认值: 10000

从 rvs 的每个可调用对象中抽取的样本数量。等效地，这是在备择假设下执行的测试次数，以近似计算功效。

批处理int, 可选

每次调用 test 时处理的样本数量。内存使用量与 batch 和最大样本大小之积成正比。默认值为 None，在这种情况下，batch 等于 n_resamples。

返回:

resPowerResult

一个带有属性的对象：

力量浮点数或ndarray

对备择假设的估计功率。

p值ndarray

在备择假设下观察到的p值。

注释

功率模拟如下：

• 在由 rvs 指定的备择假设下，绘制许多随机样本（或样本集），每个样本的大小由 n_observations 指定。

• 对于每个样本（或样本集），根据 test 计算 p 值。这些 p 值记录在结果对象的 pvalues 属性中。

• 计算p值小于 significance 水平的比例。这是结果对象 power 属性中记录的效力。

假设 significance 是一个形状为 shape1 的数组，kwargs 和 n_observations 的元素可以相互广播到形状 shape2，并且 test 返回一个形状为 shape3 的 p 值数组。那么结果对象 power 属性将是形状 shape1 + shape2 + shape3，而 pvalues 属性将是形状 shape2 + shape3 + (n_resamples,)。

示例

Try it in your browser!

假设我们希望在以下条件下模拟独立样本t检验的效力：

• 第一个样本有10个观测值，这些观测值是从均值为0的正态分布中抽取的。

• 第二个样本有12个观测值，这些观测值是从均值为1.0的正态分布中抽取的。

• 显著性p值的阈值为0.05。

>>> import numpy as np
>>> from scipy import stats
>>> rng = np.random.default_rng()
>>>
>>> test = stats.ttest_ind
>>> n_observations = (10, 12)
>>> rvs1 = rng.normal
>>> rvs2 = lambda size: rng.normal(loc=1, size=size)
>>> rvs = (rvs1, rvs2)
>>> res = stats.power(test, rvs, n_observations, significance=0.05)
>>> res.power
0.6116

分别使用大小为10和12的样本，在所选的备择假设下，显著性阈值为0.05的t检验的功效大约为60%。我们可以通过传递样本大小数组来研究样本大小对功效的影响。

>>> import matplotlib.pyplot as plt
>>> nobs_x = np.arange(5, 21)
>>> nobs_y = nobs_x
>>> n_observations = (nobs_x, nobs_y)
>>> res = stats.power(test, rvs, n_observations, significance=0.05)
>>> ax = plt.subplot()
>>> ax.plot(nobs_x, res.power)
>>> ax.set_xlabel('Sample Size')
>>> ax.set_ylabel('Simulated Power')
>>> ax.set_title('Simulated Power of `ttest_ind` with Equal Sample Sizes')
>>> plt.show()

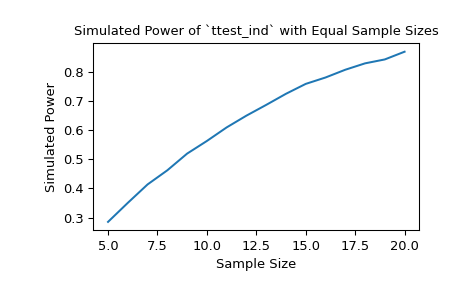
另外，我们可以研究效应量对统计功效的影响。在这种情况下，效应量是第二个样本所基于的分布的位置。

>>> n_observations = (10, 12)
>>> loc = np.linspace(0, 1, 20)
>>> rvs2 = lambda size, loc: rng.normal(loc=loc, size=size)
>>> rvs = (rvs1, rvs2)
>>> res = stats.power(test, rvs, n_observations, significance=0.05,
...                   kwargs={'loc': loc})
>>> ax = plt.subplot()
>>> ax.plot(loc, res.power)
>>> ax.set_xlabel('Effect Size')
>>> ax.set_ylabel('Simulated Power')
>>> ax.set_title('Simulated Power of `ttest_ind`, Varying Effect Size')
>>> plt.show()

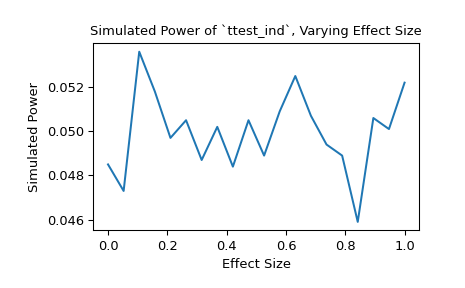
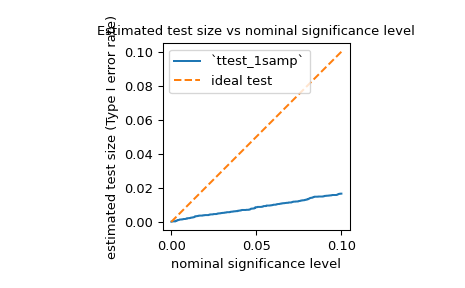
我们也可以使用 power 来估计检验的 I 类错误率（也被称为含糊的术语“大小”），并评估其是否与名义水平相匹配。例如，jarque_bera 的零假设是样本来自与正态分布具有相同偏度和峰度的分布。为了估计 I 类错误率，我们可以将零假设视为真实的*替代*假设并计算功效。

>>> test = stats.jarque_bera
>>> n_observations = 10
>>> rvs = rng.normal
>>> significance = np.linspace(0.0001, 0.1, 1000)
>>> res = stats.power(test, rvs, n_observations, significance=significance)
>>> size = res.power

如下所示，如文档中所述，对于如此小的样本，测试的I类错误率远低于名义水平。

>>> ax = plt.subplot()
>>> ax.plot(significance, size)
>>> ax.plot([0, 0.1], [0, 0.1], '--')
>>> ax.set_xlabel('nominal significance level')
>>> ax.set_ylabel('estimated test size (Type I error rate)')
>>> ax.set_title('Estimated test size vs nominal significance level')
>>> ax.set_aspect('equal', 'box')
>>> ax.legend(('`ttest_1samp`', 'ideal test'))
>>> plt.show()

正如从这样一个保守的测试中所预期的那样，相对于某些替代方案，其功效相当低。例如，在样本来自拉普拉斯分布的替代假设下，测试的功效可能不会比第一类错误率大很多。

>>> rvs = rng.laplace
>>> significance = np.linspace(0.0001, 0.1, 1000)
>>> res = stats.power(test, rvs, n_observations, significance=0.05)
>>> print(res.power)
0.0587

这不是 SciPy 实现中的错误；这只是由于测试统计量的零分布是在假设样本量较大（即趋近于无穷大）的情况下推导出来的，而对于小样本，这种渐近近似并不准确。在这种情况下，重采样和蒙特卡罗方法（例如 permutation_test、goodness_of_fit、monte_carlo_test）可能更为合适。

Go BackOpen In Tab