拟合优度#
- scipy.stats.goodness_of_fit(dist, data, *, known_params=None, fit_params=None, guessed_params=None, statistic='ad', n_mc_samples=9999, random_state=None)[源代码][源代码]#
执行一个拟合优度检验,比较数据与分布族。
给定一个分布族和数据,执行一个假设检验,即数据是从该族中的某个分布中抽取的。可以指定分布的任何已知参数。分布的剩余参数将根据数据进行拟合,并相应地计算检验的p值。有几种统计量可用于比较分布与数据。
- 参数:
- dist
scipy.stats.rv_continuous 表示零假设下分布族的对象。
- 数据1D array_like
有限、未经审查的数据待测试。
- 已知参数dict, 可选
一个包含已知分布参数的名称-值对的字典。蒙特卡罗样本从这些参数值的零假设分布中随机抽取。在计算每个蒙特卡罗样本的统计量之前,只有零假设分布族的剩余未知参数被拟合到样本中;已知参数保持不变。如果分布族的所有参数都是已知的,那么将分布族拟合到每个样本的步骤将被省略。
- fit_paramsdict, 可选
一个包含已拟合到数据的分布参数名称-值对的字典,例如使用
scipy.stats.fit或 dist 的fit方法。蒙特卡罗样本是从具有这些指定参数值的零假设分布中抽取的。然而,在这些蒙特卡罗样本上,零假设分布族的所有未知参数在统计量评估之前都会被拟合。- guessed_paramsdict, 可选
包含已猜测的分布参数名称-值对的字典。这些参数始终被视为自由参数,并且既适合提供的 data,也适合从零假设分布中抽取的蒙特卡罗样本。这些 guessed_params 的目的是用作数值拟合过程的初始值。
- 统计{“ad”, “ks”, “cvm”, “filliben”} 或可调用对象,可选
用于在将分布族的未知参数拟合到数据后,将数据与分布进行比较的统计量。Anderson-Darling(“ad”)[R48df2cf935d3-1]_、Kolmogorov-Smirnov(“ks”)[R48df2cf935d3-1]_、Cramer-von Mises(“cvm”)[R48df2cf935d3-1]_和Filliben(“filliben”)[R48df2cf935d3-7]_统计量是可用的。或者,可以提供一个带有签名``(dist, data, axis)``的可调用对象来计算统计量。这里``dist``是一个冻结的分布对象(可能带有数组参数),``data``是一个蒙特卡罗样本数组(形状兼容),``axis``是``data``上必须计算统计量的轴。
- n_mc_样本int, 默认值: 9999
从零假设分布中抽取的蒙特卡洛样本数量,以形成统计量的零分布。每个样本的大小与给定的 data 相同。
- random_state{None, int,}
用于生成蒙特卡罗样本的伪随机数生成器状态。
如果 random_state 是
None``(默认),则使用 `numpy.random.RandomState` 单例。如果 `random_state` 是整数,则使用一个新的 ``RandomState实例,并以 random_state 为种子。如果 random_state 已经是Generator或RandomState实例,则使用提供的实例。
- dist
- 返回:
- resGoodnessOfFitResult
一个具有以下属性的对象。
- fit_result
FitResult 一个表示 dist 对 data 拟合情况的对象。该对象包括了完全定义零假设分布的分布族参数值,即从中抽取蒙特卡洛样本的分布。
- 统计浮动
比较提供的 数据 与零假设分布的统计值。
- p值浮动
在零分布中,统计值至少与提供的 数据 的统计值一样极端的元素的比例。
- null_distributionndarray
从零假设分布中抽取的每个蒙特卡罗样本的统计值。
- fit_result
注释
这是一个广义的蒙特卡罗拟合优度程序,其特例对应于各种安德森-达林检验、利勒沃斯检验等。该检验在 [2]、[3] 和 [4] 中被描述为一个参数引导检验。这是一个蒙特卡罗检验,其中用于指定从中抽取样本的分布的参数已从数据中估计出来。我们使用“蒙特卡罗”而不是“参数引导”来描述该检验,以避免与更熟悉的非参数引导混淆,并在下面描述了如何执行该检验。
传统拟合优度检验
传统上,与一组固定的显著性水平相对应的临界值是使用蒙特卡罗方法预先计算的。用户通过仅计算其观测 数据 的检验统计量的值,并将此值与表格中的临界值进行比较来执行检验。这种做法不够灵活,因为表格并不适用于所有分布和已知与未知参数值的组合。此外,当临界值从有限的表格数据中插值以对应用户的样本量和拟合参数值时,结果可能不准确。为了克服这些缺点,此函数允许用户根据其特定数据执行适应的蒙特卡罗试验。
算法概述
简而言之,此例程执行以下步骤:
拟合未知参数到给定的 数据 ,从而形成“零假设”分布,并计算这对数据和分布的统计量。
从这个零假设分布中抽取随机样本。
将未知参数拟合到每个随机样本。
计算每个样本与拟合样本分布之间的统计量。
将 (1) 中与 data 对应的统计值与 (4) 中随机样本对应的统计值进行比较。p 值是统计值大于或等于观测数据统计值的样本比例。
更详细地说,步骤如下。
首先,使用最大似然估计法将 dist 指定的分布族的任何未知参数拟合到提供的 data 中。(一个例外是位置和尺度未知的正态分布:我们使用偏差校正的标准差
np.std(data, ddof=1)作为尺度,如 [1] 中所推荐的。)这些参数值指定了一个特定的分布族成员,称为“零假设分布”,即在零假设下数据被抽样的分布。statistic 用于比较数据与分布,计算 data 与零假设分布之间的差异。接下来,许多(具体为 n_mc_samples)新样本,每个样本包含与 data 相同数量的观测值,从零假设分布中抽取。分布族 dist 的所有未知参数都拟合到 每个重采样 中,并在每个样本与其对应的拟合分布之间计算 statistic。这些统计值形成了蒙特卡罗零分布(不要与上述“零假设分布”混淆)。
测试的p值是蒙特卡罗零分布中统计值的比例,这些统计值至少与提供的`数据`的统计值一样极端。更准确地说,p值由以下公式给出:
\[p = \frac{b + 1} {m + 1}\]其中 \(b\) 是蒙特卡罗零分布中大于或等于为 data 计算的统计值的统计值的数量,\(m\) 是蒙特卡罗零分布中的元素数量(n_mc_samples)。分子和分母加上 \(1\) 可以理解为将 data 对应的统计值包含在零分布中,但更正式的解释在 [5] 中给出。
限制
对于某些分布族,测试可能会非常慢,因为必须将分布族的未知参数拟合到每个蒙特卡罗样本中,而对于SciPy中的大多数分布,分布拟合是通过数值优化进行的。
反模式
因此,可能会诱使人们将预先拟合到 data`(由用户完成)的分布参数视为 `known_params,因为指定分布的所有参数可以避免将分布拟合到每个蒙特卡罗样本。(这基本上就是原始的 Kilmogorov-Smirnov 检验的执行方式。)尽管这种检验可以提供反对零假设的证据,但该检验在某种意义上是保守的,即小的 p 值往往会(大大)*高估* 犯第一类错误(即,尽管零假设为真,却拒绝了它)的概率,并且检验的效力较低(即,即使零假设为假,也不太可能拒绝它)。这是因为蒙特卡罗样本不太可能与零假设的分布以及 data 一致。这往往会增加记录在零分布中的统计量值,使得更多的统计量值超过 data 的统计量值,从而夸大了 p 值。
参考文献
[1] (1,2)M. A. Stephens (1974). “EDF Statistics for Goodness of Fit and Some Comparisons.” Journal of the American Statistical Association, Vol. 69, pp. 730-737.
[2]W. Stute, W. G. Manteiga, and M. P. Quindimil (1993). “Bootstrap based goodness-of-fit-tests.” Metrika 40.1: 243-256.
[3]C. Genest, & B Rémillard. (2008). “Validity of the parametric bootstrap for goodness-of-fit testing in semiparametric models.” Annales de l’IHP Probabilités et statistiques. Vol. 44. No. 6.
[4]I. Kojadinovic and J. Yan (2012). “Goodness-of-fit testing based on a weighted bootstrap: A fast large-sample alternative to the parametric bootstrap.” Canadian Journal of Statistics 40.3: 480-500.
[5]B. Phipson and G. K. Smyth (2010). “Permutation P-values Should Never Be Zero: Calculating Exact P-values When Permutations Are Randomly Drawn.” Statistical Applications in Genetics and Molecular Biology 9.1.
[6]H. W. Lilliefors (1967). “On the Kolmogorov-Smirnov test for normality with mean and variance unknown.” Journal of the American statistical Association 62.318: 399-402.
[7]Filliben, James J. “正态性的概率图相关系数检验。” 《Technometrics》 17.1 (1975): 111-117.
示例
一个著名的检验零假设的测试,即数据是从给定分布中抽取的,是Kolmogorov-Smirnov (KS) 测试,在SciPy中作为
scipy.stats.ks_1samp提供。假设我们希望测试以下数据:>>> import numpy as np >>> from scipy import stats >>> rng = np.random.default_rng() >>> x = stats.uniform.rvs(size=75, random_state=rng)
从正态分布中抽取样本。为了执行KS检验,观测数据的经验分布函数将与正态分布的理论累积分布函数进行比较。当然,为了做到这一点,零假设下的正态分布必须完全指定。这通常通过首先将分布的``loc``和``scale``参数拟合到观测数据,然后执行检验来完成。
>>> loc, scale = np.mean(x), np.std(x, ddof=1) >>> cdf = stats.norm(loc, scale).cdf >>> stats.ks_1samp(x, cdf) KstestResult(statistic=0.1119257570456813, pvalue=0.2827756409939257, statistic_location=0.7751845155861765, statistic_sign=-1)
KS-test 的一个优点是,p 值——在零假设下,获得与观测数据中获得的值一样极端的检验统计值的概率——可以被精确且高效地计算出来。
goodness_of_fit只能近似这些结果。>>> known_params = {'loc': loc, 'scale': scale} >>> res = stats.goodness_of_fit(stats.norm, x, known_params=known_params, ... statistic='ks', random_state=rng) >>> res.statistic, res.pvalue (0.1119257570456813, 0.2788)
统计数据完全匹配,但 p 值是通过形成一个“蒙特卡罗零分布”来估计的,也就是说,通过从
scipy.stats.norm中显式地抽取随机样本,并使用提供的参数计算每个样本的统计数据。这些统计值中至少与res.statistic一样极端的比例近似于scipy.stats.ks_1samp计算的精确 p 值。然而,在许多情况下,我们更倾向于测试数据是否从正态分布家族的*任何*成员中抽取,而不是特别从根据观察样本拟合的位置和尺度参数的正态分布中抽取。在这种情况下,Lilliefors [6] 认为KS检验过于保守(即p值夸大了实际拒绝真实零假设的概率),因此缺乏效力——即在零假设实际上为假时拒绝零假设的能力。实际上,我们上面的p值大约为0.28,这在任何常见的显著性水平上都无法拒绝零假设。
考虑为什么会这样。注意在上面的KS检验中,统计量总是将数据与拟合到*观测数据*的正态分布的CDF进行比较。这往往会降低观测数据的统计量值,但在计算其他样本(如我们随机抽取以形成蒙特卡罗零分布的样本)的统计量时,这是“不公平”的。很容易纠正这一点:每当我们计算一个样本的KS统计量时,我们都使用拟合到*该样本*的正态分布的CDF。在这种情况下,零分布尚未被精确计算,通常如上所述使用蒙特卡罗方法进行近似。这就是`goodness_of_fit`表现出色的地方。
>>> res = stats.goodness_of_fit(stats.norm, x, statistic='ks', ... random_state=rng) >>> res.statistic, res.pvalue (0.1119257570456813, 0.0196)
确实,这个p值要小得多,并且小到足以(正确地)在常见的显著性水平上拒绝零假设,包括5%和2.5%。
然而,KS统计量对所有偏离正态性的情况并不十分敏感。KS统计量最初的优势在于能够理论上计算零分布,但现在我们可以通过计算近似零分布,使用一个更敏感的统计量——从而提高测试功效。Anderson-Darling统计量 [1] 往往更为敏感,并且通过蒙特卡罗方法,该统计量的临界值已针对不同的显著性水平和样本量进行了制表。
>>> res = stats.anderson(x, 'norm') >>> print(res.statistic) 1.2139573337497467 >>> print(res.critical_values) [0.549 0.625 0.75 0.875 1.041] >>> print(res.significance_level) [15. 10. 5. 2.5 1. ]
在这里,统计量的观测值超过了与1%显著性水平对应的临界值。这告诉我们观测数据的p值小于1%,但它具体是多少呢?我们可以从这些(已经插值的)值中进行插值,但
goodness_of_fit可以直接估计它。>>> res = stats.goodness_of_fit(stats.norm, x, statistic='ad', ... random_state=rng) >>> res.statistic, res.pvalue (1.2139573337497467, 0.0034)
进一步的优势是,使用
goodness_of_fit并不局限于特定的分布集合或已知参数与必须从数据中估计的参数的条件。相反,goodness_of_fit可以相对快速地为任何具有足够快速和可靠的fit方法的分布估计 p 值。例如,这里我们使用 Cramer-von Mises 统计量对已知位置和未知尺度的瑞利分布进行拟合优度检验。>>> rng = np.random.default_rng() >>> x = stats.chi(df=2.2, loc=0, scale=2).rvs(size=1000, random_state=rng) >>> res = stats.goodness_of_fit(stats.rayleigh, x, statistic='cvm', ... known_params={'loc': 0}, random_state=rng)
这个执行得相当快,但为了检查
fit方法的可靠性,我们应该检查拟合结果。>>> res.fit_result # location is as specified, and scale is reasonable params: FitParams(loc=0.0, scale=2.1026719844231243) success: True message: 'The fit was performed successfully.' >>> import matplotlib.pyplot as plt # matplotlib must be installed to plot >>> res.fit_result.plot() >>> plt.show()
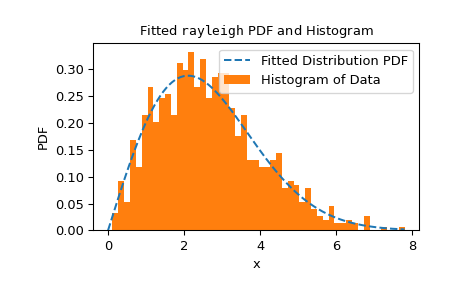
如果分布不能尽可能好地拟合观测数据,测试可能无法控制I类错误率,即即使在零假设为真时拒绝它的可能性。
我们还应该在零分布中寻找可能由不可靠拟合引起的极端异常值。这些并不一定会使结果无效,但它们往往会降低测试的效力。
>>> _, ax = plt.subplots() >>> ax.hist(np.log10(res.null_distribution)) >>> ax.set_xlabel("log10 of CVM statistic under the null hypothesis") >>> ax.set_ylabel("Frequency") >>> ax.set_title("Histogram of the Monte Carlo null distribution") >>> plt.show()
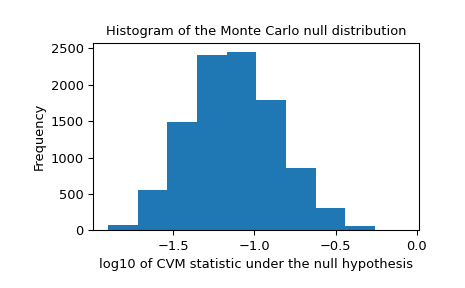
这个图看起来令人安心。
如果
fit方法工作可靠,并且如果检验统计量的分布对拟合参数的值不特别敏感,那么goodness_of_fit提供的 p 值预计会是一个很好的近似值。>>> res.statistic, res.pvalue (0.2231991510248692, 0.0525)