scipy.stats.

rv_histogram

class scipy.stats.rv_histogram(histogram, *args, density=None, **kwargs)

生成由直方图给出的分布。这对于从分箱数据样本生成模板分布非常有用。

作为 rv_continuous 类的子类，rv_histogram 继承了它的一系列通用方法（详见 rv_continuous 的完整列表），并基于提供的分箱数据样本的属性实现了这些方法。

参数:

直方图数组类元组

包含两个类数组对象的元组。第一个包含 n 个箱的内容，第二个包含 (n+1) 个箱边界。特别是，numpy.histogram 的返回值可以被接受。

密度bool, 可选

如果为 False，则假设直方图与每个箱子的计数成比例；否则，假设它与密度成比例。对于恒定的箱宽，这两者是等价的，但在箱宽变化时，这种区别很重要（参见注释）。如果为 None（默认），则设置 density=True 以保持向后兼容性，但如果箱宽可变，则会发出警告。显式设置 density 以消除警告。

Added in version 1.10.0.

属性:

random_state

获取或设置用于生成随机变量的生成器对象。

方法

__call__(*args, **kwds)	冻结给定参数的发行版。
cdf(x, *args, **kwds)	给定随机变量的累积分布函数。
entropy(*args, **kwds)	随机变量的微分熵。
expect([func, args, loc, scale, lb, ub, ...])	通过数值积分计算函数相对于分布的期望值。
fit(data, *args, **kwds)	从数据中返回形状（如果适用）、位置和尺度参数的估计值。
fit_loc_scale(data, *args)	使用数据的第1和第2矩估计位置和尺度参数。
freeze(*args, **kwds)	冻结给定参数的发行版。
interval(confidence, *args, **kwds)	在中位数周围等面积的置信区间。
isf(q, *args, **kwds)	给定随机变量在 q 处的逆生存函数（sf 的逆）。
logcdf(x, *args, **kwds)	给定随机变量在 x 处的累积分布函数的对数。
logpdf(x, *args, **kwds)	给定随机变量在 x 处的概率密度函数的对数。
logsf(x, *args, **kwds)	给定随机变量的生存函数的对数。
mean(*args, **kwds)	分布的均值。
median(*args, **kwds)	分布的中位数。
moment(order, *args, **kwds)	指定阶数的分布非中心矩。
nnlf(theta, x)	负对数似然函数。
pdf(x, *args, **kwds)	给定随机变量在 x 处的概率密度函数。
ppf(q, *args, **kwds)	百分位点函数（cdf 的逆函数）在给定随机变量 RV 的 q 处的值。
rvs(*args, **kwds)	给定类型的随机变量。
sf(x, *args, **kwds)	生存函数（1 - cdf）在给定随机变量 RV 的 x 处的值。
stats(*args, **kwds)	给定RV的一些统计数据。
std(*args, **kwds)	分布的标准差。
support(*args, **kwargs)	对发行版的支持。
var(*args, **kwds)	分布的方差。

注释

当直方图的区间宽度不均匀时，区分按区间计数的直方图和按区间概率密度成比例的直方图是有区别的。如果调用 numpy.histogram 时使用其默认的 density=False，则生成的直方图是每个区间的计数，因此应将 density=False 传递给 rv_histogram。如果调用 numpy.histogram 时使用 density=True，则生成的直方图是按概率密度计算的，因此应将 density=True 传递给 rv_histogram。为避免警告，当输入的直方图具有不均匀的区间宽度时，始终显式传递 density。

除了位置和尺度参数外，没有额外的形状参数。概率密度函数（pdf）是根据提供的直方图定义的分段函数。累积分布函数（cdf）是pdf的线性插值。

Added in version 0.19.0.

示例

Try it in your browser!

从 numpy 直方图创建一个 scipy.stats 分布

>>> import scipy.stats
>>> import numpy as np
>>> data = scipy.stats.norm.rvs(size=100000, loc=0, scale=1.5,
...                             random_state=123)
>>> hist = np.histogram(data, bins=100)
>>> hist_dist = scipy.stats.rv_histogram(hist, density=False)

表现得像一个普通的 scipy rv_continuous 分布

>>> hist_dist.pdf(1.0)
0.20538577847618705
>>> hist_dist.cdf(2.0)
0.90818568543056499

PDF 在直方图的最高（最低）区间之上（之下）为零，该区间由原始数据集的最大（最小）值定义。

>>> hist_dist.pdf(np.max(data))
0.0
>>> hist_dist.cdf(np.max(data))
1.0
>>> hist_dist.pdf(np.min(data))
7.7591907244498314e-05
>>> hist_dist.cdf(np.min(data))
0.0

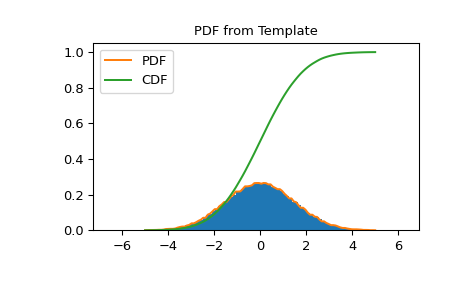
PDF 和 CDF 遵循直方图

>>> import matplotlib.pyplot as plt
>>> X = np.linspace(-5.0, 5.0, 100)
>>> fig, ax = plt.subplots()
>>> ax.set_title("PDF from Template")
>>> ax.hist(data, density=True, bins=100)
>>> ax.plot(X, hist_dist.pdf(X), label='PDF')
>>> ax.plot(X, hist_dist.cdf(X), label='CDF')
>>> ax.legend()
>>> fig.show()

Go BackOpen In Tab