scipy.stats.vonmises

scipy.stats.vonmises = <scipy.stats._continuous_distns.vonmises_gen object>

冯·米塞斯连续随机变量。

作为 rv_continuous 类的一个实例，vonmises 对象继承了它的一系列通用方法（完整列表见下文），并根据此特定分布的细节对其进行了补充。

方法

rvs(kappa, loc=0, scale=1, size=1, random_state=None)	随机变量。
pdf(x, kappa, loc=0, scale=1)	概率密度函数。
logpdf(x, kappa, loc=0, scale=1)	概率密度函数的对数。
cdf(x, kappa, loc=0, scale=1)	累积分布函数。
logcdf(x, kappa, loc=0, scale=1)	累积分布函数的对数。
sf(x, kappa, loc=0, scale=1)	生存函数 (也定义为 1 - cdf，但 sf 有时更精确)。
logsf(x, kappa, loc=0, scale=1)	生存函数的对数。
ppf(q, kappa, loc=0, scale=1)	百分点函数（cdf 的逆函数 — 百分位数）。
isf(q, kappa, loc=0, scale=1)	逆生存函数（sf 的逆函数）。
moment(order, kappa, loc=0, scale=1)	指定阶数的非中心矩。
stats(kappa, loc=0, scale=1, moments=’mv’)	均值(‘m’)、方差(‘v’)、偏度(‘s’) 和/或 峰度(‘k’)。
entropy(kappa, loc=0, scale=1)	（微分）随机变量的熵。
fit(data)	通用数据的参数估计。有关关键字参数的详细文档，请参见 scipy.stats.rv_continuous.fit 。
expect(func, args=(kappa,), loc=0, scale=1, lb=None, ub=None, conditional=False, **kwds)	函数（单参数）相对于分布的期望值。
median(kappa, loc=0, scale=1)	分布的中位数。
mean(kappa, loc=0, scale=1)	分布的均值。
var(kappa, loc=0, scale=1)	分布的方差。
std(kappa, loc=0, scale=1)	分布的标准差。
interval(confidence, kappa, loc=0, scale=1)	在中位数周围等面积的置信区间。

参见

scipy.stats.vonmises_fisher

超球面上的冯·米塞斯-费舍尔分布

注释

vonmises 和 vonmises_line 的概率密度函数为：

\[f(x, \kappa) = \frac{ \exp(\kappa \cos(x)) }{ 2 \pi I_0(\kappa) }\]

对于 \(-\pi \le x \le \pi\), \(\kappa \ge 0\)。\(I_0\) 是零阶修正贝塞尔函数（scipy.special.i0）。

vonmises 是一种不将分布限制在固定区间的圆形分布。目前，SciPy 中没有圆形分布框架。cdf 的实现方式是 cdf(x + 2*np.pi) == cdf(x) + 1。

vonmises_line 是相同的分布，定义在实数轴上的 \([-\pi, \pi]\) 区间。这是一个常规（即非循环）分布。

关于分布参数的说明：vonmises 和 vonmises_line 将 kappa 作为形状参数（浓度），将 loc 作为位置（循环均值）。接受 scale 参数，但没有任何效果。

示例

Try it in your browser!

导入必要的模块。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.stats import vonmises

定义分布参数。

>>> loc = 0.5 * np.pi  # circular mean
>>> kappa = 1  # concentration

通过 pdf 方法计算 x=0 处的概率密度。

>>> vonmises.pdf(0, loc=loc, kappa=kappa)
0.12570826359722018

验证百分位函数 ppf 在浮点精度范围内反转累积分布函数 cdf。

>>> x = 1
>>> cdf_value = vonmises.cdf(x, loc=loc, kappa=kappa)
>>> ppf_value = vonmises.ppf(cdf_value, loc=loc, kappa=kappa)
>>> x, cdf_value, ppf_value
(1, 0.31489339900904967, 1.0000000000000004)

通过调用 rvs 方法绘制1000个随机变量。

>>> sample_size = 1000
>>> sample = vonmises(loc=loc, kappa=kappa).rvs(sample_size)

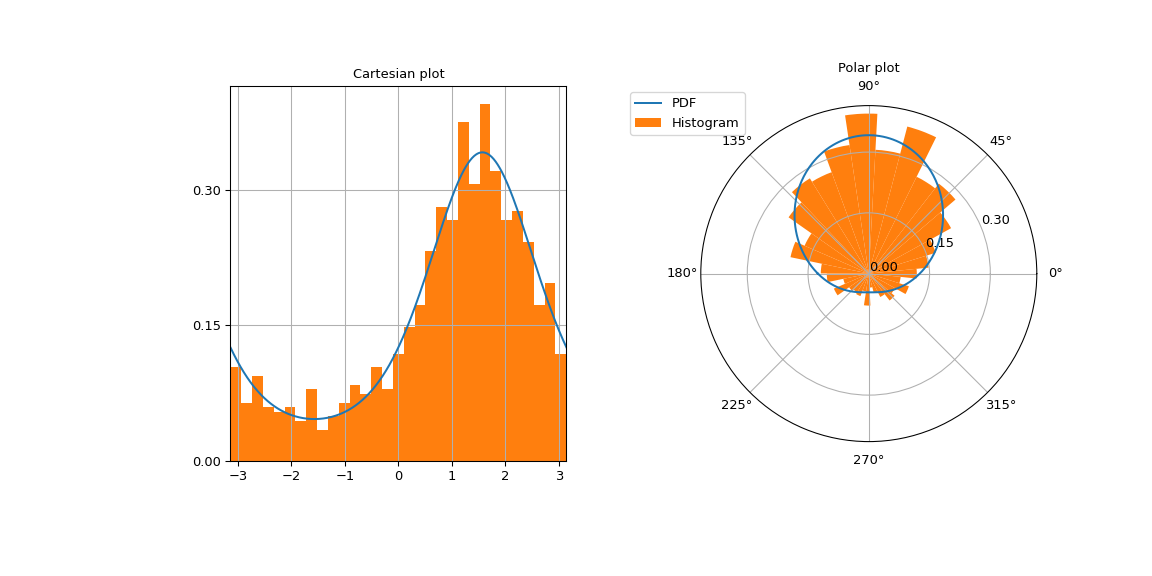
在笛卡尔和极坐标网格上绘制 von Mises 密度，以强调它是一个圆形分布。

>>> fig = plt.figure(figsize=(12, 6))
>>> left = plt.subplot(121)
>>> right = plt.subplot(122, projection='polar')
>>> x = np.linspace(-np.pi, np.pi, 500)
>>> vonmises_pdf = vonmises.pdf(x, loc=loc, kappa=kappa)
>>> ticks = [0, 0.15, 0.3]

左侧图像包含笛卡尔坐标图。

>>> left.plot(x, vonmises_pdf)
>>> left.set_yticks(ticks)
>>> number_of_bins = int(np.sqrt(sample_size))
>>> left.hist(sample, density=True, bins=number_of_bins)
>>> left.set_title("Cartesian plot")
>>> left.set_xlim(-np.pi, np.pi)
>>> left.grid(True)

右侧图像包含极坐标图。

>>> right.plot(x, vonmises_pdf, label="PDF")
>>> right.set_yticks(ticks)
>>> right.hist(sample, density=True, bins=number_of_bins,
...            label="Histogram")
>>> right.set_title("Polar plot")
>>> right.legend(bbox_to_anchor=(0.15, 1.06))

Go BackOpen In Tab