插值过渡指南

本页包含三组演示：

• 为 scipy.interpolate.interp2d 提供的低级 FITPACK 替换，用于与 scipy.interpolate.interp2d 的遗留错误兼容的替换；

• 在新代码中推荐使用的 scipy.interpolate.interp2d 的替代方法；

• 2D FITPACK 基础线性插值的故障模式演示及推荐的替代方案。

1. How to transition away from using interp2d

interp2d 在二维规则网格上的插值和二维散点数据的插值之间静默切换。切换基于（展开的）x、y 和 z 数组的长度。简而言之，对于规则网格使用 scipy.interpolate.RectBivariateSpline；对于散点插值，使用 bisprep/bisplev 组合。下面我们给出了逐点过渡的示例，这应该能完全保留 interp2d 的结果。

1.1 在规则网格上的 interp2d

我们从（稍作修改的）文档字符串示例开始。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import interp2d, RectBivariateSpline

>>> x = np.arange(-5.01, 5.01, 0.25)
>>> y = np.arange(-5.01, 7.51, 0.25)
>>> xx, yy = np.meshgrid(x, y)
>>> z = np.sin(xx**2 + 2.*yy**2)
>>> f = interp2d(x, y, z, kind='cubic')

这是“常规网格”代码路径，因为

>>> z.size == len(x) * len(y)
True

另外，请注意 x.size != y.size：

>>> x.size, y.size
(41, 51)

现在，让我们构建一个便利函数来构造插值器并绘制它。

>>> def plot(f, xnew, ynew):
...    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4))
...    znew = f(xnew, ynew)
...    ax1.plot(x, z[0, :], 'ro-', xnew, znew[0, :], 'b-')
...    im = ax2.imshow(znew)
...    plt.colorbar(im, ax=ax2)
...    plt.show()
...    return znew
...
>>> xnew = np.arange(-5.01, 5.01, 1e-2)
>>> ynew = np.arange(-5.01, 7.51, 1e-2)
>>> znew_i = plot(f, xnew, ynew)

替换：使用 RectBivariateSpline，结果相同

注意转置：首先，在构造函数中，其次，你需要转置评估的结果。这是为了撤销 interp2d 所做的转置。

>>> r = RectBivariateSpline(x, y, z.T)
>>> rt = lambda xnew, ynew: r(xnew, ynew).T
>>> znew_r = plot(rt, xnew, ynew)

>>> from numpy.testing import assert_allclose
>>> assert_allclose(znew_i, znew_r, atol=1e-14)

插值顺序：线性、立方等

interp2d 默认使用 kind="linear"，即在 x- 和 y- 方向上均为线性插值。而 RectBivariateSpline 则默认使用三次插值，kx=3, ky=3。

这里是完全等价的关系：

interp2d	RectBivariateSpline
无关键字参数	kx = 1, ky = 1
kind=’linear’	kx = 1, ky = 1
kind=’cubic’	kx = 3, ky = 3

1.2. 使用 interp2d 进行点全坐标插值（散点插值）

在这里，我们将前一个练习中的网格扁平化以说明其功能。

>>> xxr = xx.ravel()
>>> yyr = yy.ravel()
>>> zzr = z.ravel()
>>> f = interp2d(xxr, yyr, zzr, kind='cubic')

注意，这是“非规则网格”代码路径，适用于分散数据，其中 len(x) == len(y) == len(z)。

>>> len(xxr) == len(yyr) == len(zzr)
True

>>> xnew = np.arange(-5.01, 5.01, 1e-2)
>>> ynew = np.arange(-5.01, 7.51, 1e-2)
>>> znew_i = plot(f, xnew, ynew)

替换：直接使用 scipy.interpolate.bisplrep / scipy.interpolate.bisplev

>>> from scipy.interpolate import bisplrep, bisplev
>>> tck = bisplrep(xxr, yyr, zzr, kx=3, ky=3, s=0)
# convenience: make up a callable from bisplev
>>> ff = lambda xnew, ynew: bisplev(xnew, ynew, tck).T   # Note the transpose, to mimic what interp2d does
>>> znew_b = plot(ff, xnew, ynew)

>>> assert_allclose(znew_i, znew_b, atol=1e-15)

插值顺序：线性、立方等

interp2d 默认使用 kind="linear"，即在 x- 和 y- 方向上均为线性。而 bisplrep 则默认使用三次插值，kx=3, ky=3。

这里是完全等价的关系：

interp2d	bisplrep
无关键字参数	kx = 1, ky = 1
kind=’linear’	kx = 1, ky = 1
kind=’cubic’	kx = 3, ky = 3

2. Alternative to interp2d: regular grid

对于新代码，推荐的替代方案是 RegularGridInterpolator。这是一个独立的实现，不基于 FITPACK。支持最近邻、线性插值和奇数阶张量积样条。

样条结点保证与数据点重合。

请注意，这里：

1. 元组参数是 (x, y)

2. z 数组需要转置

3. 关键字名称是 method，而不是 kind。

4. bounds_error 参数默认为 True。

>>> from scipy.interpolate import RegularGridInterpolator as RGI
>>> r = RGI((x, y), z.T, method='linear', bounds_error=False)

评估：创建一个二维网格。使用 indexing=’ij’ 和 sparse=True 来节省一些内存：

>>> xxnew, yynew = np.meshgrid(xnew, ynew, indexing='ij', sparse=True)

评估，注意元组参数：

>>> znew_reggrid = r((xxnew, yynew))

>>> fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4))
# Again, note the transpose to undo the `interp2d` convention
>>> znew_reggrid_t = znew_reggrid.T
>>> ax1.plot(x, z[0, :], 'ro-', xnew, znew_reggrid_t[0, :], 'b-')
>>> im = ax2.imshow(znew_reggrid_t)
>>> plt.colorbar(im, ax=ax2)

3. Scattered 2D linear interpolation: prefer LinearNDInterpolator to SmoothBivariateSpline or bisplrep

对于二维散点线性插值，SmoothBivariateSpline 和 biplrep 可能会发出警告，或者无法插值数据，或者生成远离数据点的节点。相反，建议使用 LinearNDInterpolator，它基于通过 QHull 对数据进行三角剖分。

# TestSmoothBivariateSpline::test_integral
>>> from scipy.interpolate import SmoothBivariateSpline, LinearNDInterpolator
>>> x = np.array([1,1,1,2,2,2,4,4,4])
>>> y = np.array([1,2,3,1,2,3,1,2,3])
>>> z = np.array([0,7,8,3,4,7,1,3,4])

现在，使用基于Qhull的数据三角剖分的线性插值：

>>> xy = np.c_[x, y]   # or just list(zip(x, y))
>>> lut2 = LinearNDInterpolator(xy, z)
>>> X = np.linspace(min(x), max(x))
>>> Y = np.linspace(min(y), max(y))
>>> X, Y = np.meshgrid(X, Y)

结果易于理解和解释：

>>> fig = plt.figure()
>>> ax = fig.add_subplot(projection='3d')
>>> ax.plot_wireframe(X, Y, lut2(X, Y))
>>> ax.scatter(x, y, z,  'o', color='k', s=48)

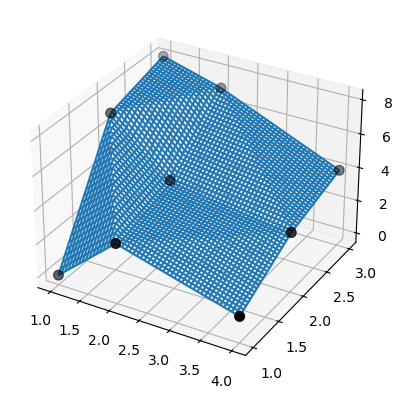
注意 bisplrep 做的事情不同！它可能会将样条结点放置在数据范围之外。

为了说明，考虑来自上一个示例的相同数据：

>>> tck = bisplrep(x, y, z, kx=1, ky=1, s=0)
>>> fig = plt.figure()
>>> ax = fig.add_subplot(projection='3d')
>>> xx = np.linspace(min(x), max(x))
>>> yy = np.linspace(min(y), max(y))
>>> X, Y = np.meshgrid(xx, yy)
>>> Z = bisplev(xx, yy, tck)
>>> Z = Z.reshape(*X.shape).T
>>> ax.plot_wireframe(X, Y, Z, rstride=2, cstride=2)
>>> ax.scatter(x, y, z,  'o', color='k', s=48)

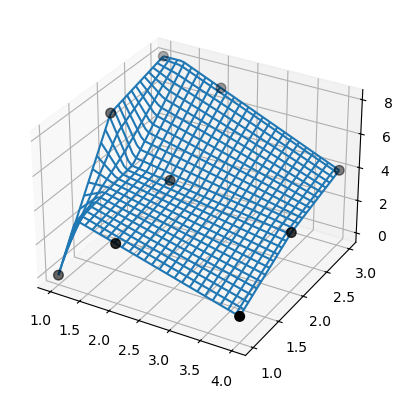
此外，SmoothBivariateSpline 未能插值数据。再次使用与前一个示例相同的数据。

>>> lut = SmoothBivariateSpline(x, y, z, kx=1, ky=1, s=0)
>>> fig = plt.figure()
>>> ax = fig.add_subplot(projection='3d')
>>> xx = np.linspace(min(x), max(x))
>>> yy = np.linspace(min(y), max(y))
>>> X, Y = np.meshgrid(xx, yy)
>>> ax.plot_wireframe(X, Y, lut(xx, yy).T, rstride=4, cstride=4)
>>> ax.scatter(x, y, z,  'o', color='k', s=48)

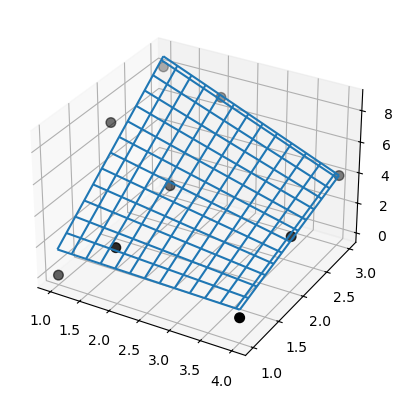
注意，与 LinearNDInterpolator 的结果不同，SmoothBivariateSpline 和 bisplrep 的结果都有瑕疵。这里展示的问题是在线性插值中报告的，然而 FITPACK 的节点选择机制并不能保证在高阶（例如三次）样条曲面中避免这些问题。