线性代数 (`scipy.linalg`)#

当使用优化的 ATLAS LAPACK 和 BLAS 库构建 SciPy 时，它具有非常快速的线性代数功能。如果你深入挖掘，所有原始的 LAPACK 和 BLAS 库都可以供你使用，以获得更快的速度。在本节中，将介绍一些更易于使用的这些例程的接口。

所有这些线性代数例程都期望一个可以转换为二维数组的对象。这些例程的输出也是一个二维数组。

scipy.linalg vs numpy.linalg#

scipy.linalg 包含 numpy.linalg 中的所有函数，以及 numpy.linalg 中不包含的一些更高级的函数。

使用 scipy.linalg 而不是 numpy.linalg 的另一个优势是，它总是使用 BLAS/LAPACK 支持编译的，而 NumPy 则是可选的。因此，SciPy 版本可能会更快，具体取决于 NumPy 的安装方式。

因此，除非你不希望将 scipy 作为依赖项添加到你的 numpy 程序中，否则请使用 scipy.linalg 而不是 numpy.linalg。

numpy.matrix vs 2-D numpy.ndarray#

表示矩阵的类以及基本操作，如矩阵乘法和转置，是 numpy 的一部分。为了方便起见，我们在这里总结了 numpy.matrix 和 numpy.ndarray 之间的区别。

numpy.matrix 是一个矩阵类，它比 numpy.ndarray 具有更方便的接口，用于矩阵操作。例如，该类支持通过分号创建 MATLAB 风格的语法，默认情况下 * 运算符表示矩阵乘法，并且包含 I 和 T 成员，它们分别是逆和转置的快捷方式：

>>> import numpy as np

>>> A = np.asmatrix('[1 2;3 4]')
>>> A
matrix([[1, 2],
        [3, 4]])
>>> A.I
matrix([[-2. ,  1. ],
        [ 1.5, -0.5]])
>>> b = np.asmatrix('[5 6]')
>>> b
matrix([[5, 6]])
>>> b.T
matrix([[5],
        [6]])
>>> A*b.T
matrix([[17],
        [39]])

尽管使用 numpy.matrix 类很方便，但不推荐使用，因为它并没有增加任何不能通过二维 numpy.ndarray 对象实现的功能，而且可能会导致混淆正在使用的类。例如，上述代码可以重写为：

>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1,2],[3,4]])
>>> A
array([[1, 2],
      [3, 4]])
>>> linalg.inv(A)
array([[-2. ,  1. ],
      [ 1.5, -0.5]])
>>> b = np.array([[5,6]]) #2D 数组
>>> b
array([[5, 6]])
>>> b.T
array([[5],
      [6]])
>>> A*b #不是矩阵乘法！
array([[ 5, 12],
      [15, 24]])
>>> A.dot(b.T) #矩阵乘法
array([[17],
      [39]])
>>> b = np.array([5,6]) #1D 数组
>>> b
array([5, 6])
>>> b.T  #不是矩阵转置！
array([5, 6])
>>> A.dot(b)  #对乘法没有影响
array([17, 39])

scipy.linalg 操作可以同样应用于 numpy.matrix 或二维 numpy.ndarray 对象。

基本例程#

求逆矩阵#

矩阵 \(\mathbf{A}\) 的逆矩阵是 \(\mathbf{B}\)，使得 \(\mathbf{AB}=\mathbf{I}\)，其中 \(\mathbf{I}\) 是主对角线上为1的单位矩阵。通常，\(\mathbf{B}\) 表示为 \(\mathbf{B}=\mathbf{A}^{-1}\)。在 SciPy 中，NumPy 数组 A 的逆矩阵可以通过 linalg.inv (A) 获得，或者如果 A 是 Matrix，则可以使用 A.I。例如，设

\[\begin{split}\mathbf{A} = \left[\begin{array}{ccc} 1 & 3 & 5\\ 2 & 5 & 1\\ 2 & 3 & 8\end{array}\right],\end{split}\]

那么

\[\begin{split}\mathbf{A^{-1}} = \frac{1}{25} \left[\begin{array}{ccc} -37 & 9 & 22 \\ 14 & 2 & -9 \\ 4 & -3 & 1 \end{array}\right] = % \left[\begin{array}{ccc} -1.48 & 0.36 & 0.88 \\ 0.56 & 0.08 & -0.36 \\ 0.16 & -0.12 & 0.04 \end{array}\right].\end{split}\]

以下示例演示了在SciPy中进行此计算

>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1,3,5],[2,5,1],[2,3,8]])
>>> A
array([[1, 3, 5],
      [2, 5, 1],
      [2, 3, 8]])
>>> linalg.inv(A)
array([[-1.48,  0.36,  0.88],
      [ 0.56,  0.08, -0.36],
      [ 0.16, -0.12,  0.04]])
>>> A.dot(linalg.inv(A)) #双重检查
array([[  1.00000000e+00,  -1.11022302e-16,  -5.55111512e-17],
      [  3.05311332e-16,   1.00000000e+00,   1.87350135e-16],
      [  2.22044605e-16,  -1.11022302e-16,   1.00000000e+00]])

求解线性系统#

使用scipy命令 linalg.solve 求解线性方程组非常直接。该命令期望输入一个矩阵和一个右侧向量。然后计算解向量。提供了一个输入对称矩阵的选项，在适用的情况下可以加快处理速度。例如，假设我们希望求解以下联立方程：

\begin{eqnarray*} x + 3y + 5z & = & 10 \\ 2x + 5y + z & = & 8 \\ 2x + 3y + 8z & = & 3 \end{eqnarray*}

我们可以使用矩阵逆来找到解向量：

\[\begin{split}\left[\begin{array}{c} x\\ y\\ z\end{array}\right]=\left[\begin{array}{ccc} 1 & 3 & 5\\ 2 & 5 & 1\\ 2 & 3 & 8\end{array}\right]^{-1}\left[\begin{array}{c} 10\\ 8\\ 3\end{array}\right]=\frac{1}{25}\left[\begin{array}{c} -232\\ 129\\ 19\end{array}\right]=\left[\begin{array}{c} -9.28\\ 5.16\\ 0.76\end{array}\right].\end{split}\]

然而，使用 linalg.solve 命令会更好，因为它可以更快且在数值上更稳定。在这种情况下，它给出的答案与以下示例所示相同：

>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1, 2], [3, 4]])
>>> A
array([[1, 2],
      [3, 4]])
>>> b = np.array([[5], [6]])
>>> b
array([[5],
      [6]])
>>> linalg.inv(A).dot(b)  # 慢
array([[-4. ],
      [ 4.5]])
>>> A.dot(linalg.inv(A).dot(b)) - b  # 检查
array([[  8.88178420e-16],
      [  2.66453526e-15]])
>>> np.linalg.solve(A, b)  # 快
array([[-4. ],
      [ 4.5]])
>>> A.dot(np.linalg.solve(A, b)) - b  # 检查
array([[ 0.],
      [ 0.]])

计算行列式#

方阵 \(\mathbf{A}\) 的行列式通常表示为 \(\left|\mathbf{A}\right|\)，是线性代数中常用的一个量。假设 \(a_{ij}\) 是矩阵 \(\mathbf{A}\) 的元素，并且令 \(M_{ij}=\left|\mathbf{A}_{ij}\right|\) 为从 \(\mathbf{A}\) 中移除第 \(i^{\textrm{th}}\) 行和第 \(j^{\textrm{th}}\) 列后得到的矩阵的行列式。那么，对于任意行 \(i,\)

\[\left|\mathbf{A}\right|=\sum_{j}\left(-1\right)^{i+j}a_{ij}M_{ij}.\]

这是一种递归定义行列式的方法，其中基本情况是通过接受 \(1\times1\) 矩阵的行列式就是该矩阵的唯一元素来定义的。在 SciPy 中，行列式可以通过 linalg.det 计算。例如，行列式为

\[\begin{split}\mathbf{A=}\left[\begin{array}{ccc} 1 & 3 & 5\\ 2 & 5 & 1\\ 2 & 3 & 8\end{array}\right]\end{split}\]

是

\begin{eqnarray*} \left|\mathbf{A}\right| & = & 1\left|\begin{array}{cc} 5 & 1\\ 3 & 8\end{array}\right|-3\left|\begin{array}{cc} 2 & 1\\ 2 & 8\end{array}\right|+5\left|\begin{array}{cc} 2 & 5\\ 2 & 3\end{array}\right|\\ & = & 1\left(5\cdot8-3\cdot1\right)-3\left(2\cdot8-2\cdot1\right)+5\left(2\cdot3-2\cdot5\right)=-25.\end{eqnarray*}.

在 SciPy 中，这是按以下示例计算的：

>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1,2],[3,4]])
>>> A
array([[1, 2],
      [3, 4]])
>>> linalg.det(A)
-2.0

计算范数#

矩阵和向量的范数也可以使用 SciPy 计算。通过 linalg.norm 的 order 参数，可以使用多种范数定义。此函数接受一个秩为 1（向量）或秩为 2（矩阵）的数组以及一个可选的 order 参数（默认值为 2）。根据这些输入，将计算请求的阶数的向量或矩阵范数。

对于向量 x，order 参数可以是任何实数，包括 inf 或 -inf。计算的范数为

\[\begin{split}\left\Vert \mathbf{x}\right\Vert =\left\{ \begin{array}{cc} \max\left|x_{i}\right| & \textrm{ord}=\textrm{inf}\\ \min\left|x_{i}\right| & \textrm{ord}=-\textrm{inf}\\ \left(\sum_{i}\left|x_{i}\right|^{\textrm{ord}}\right)^{1/\textrm{ord}} & \left|\textrm{ord}\right|<\infty.\end{array}\right.\end{split}\]

对于矩阵 \(\mathbf{A}\)，norm 的有效值仅为 \(\pm2,\pm1,\) \(\pm\) inf 和 ‘fro’（或 ‘f’）。因此，

\[\begin{split}\left\Vert \mathbf{A}\right\Vert =\left\{ \begin{array}{cc} \max_{i}\sum_{j}\left|a_{ij}\right| & \textrm{ord}=\textrm{inf}\\ \min_{i}\sum_{j}\left|a_{ij}\right| & \textrm{ord}=-\textrm{inf}\\ \max_{j}\sum_{i}\left|a_{ij}\right| & \textrm{ord}=1\\ \min_{j}\sum_{i}\left|a_{ij}\right| & \textrm{ord}=-1\\ \max\sigma_{i} & \textrm{ord}=2\\ \min\sigma_{i} & \textrm{ord}=-2\\ \sqrt{\textrm{trace}\left(\mathbf{A}^{H}\mathbf{A}\right)} & \textrm{ord}=\textrm{'fro'}\end{array}\right.\end{split}\]

其中 \(\sigma_{i}\) 是 \(\mathbf{A}\) 的奇异值。

示例:

>>> import numpy as np
>>> from scipy import linalg
>>> A=np.array([[1,2],[3,4]])
>>> A
array([[1, 2],
      [3, 4]])
>>> linalg.norm(A)
5.4772255750516612
>>> linalg.norm(A,'fro') # Frobenius 范数是默认值
5.4772255750516612
>>> linalg.norm(A,1) # L1 范数（最大列和）
6
>>> linalg.norm(A,-1)
4
>>> linalg.norm(A,np.inf) # L inf 范数（最大行和）
7

求解线性最小二乘问题和伪逆#

线性最小二乘问题出现在应用数学的许多分支中。在这个问题中，寻求一组线性缩放系数，使得模型能够拟合数据。特别地，假设数据 \(y_{i}\) 与数据 \(\mathbf{x}_{i}\) 通过一组系数 \(c_{j}\) 和模型函数 \(f_{j}\left(\mathbf{x}_{i}\right)\) 通过模型相关联

\[y_{i}=\sum_{j}c_{j}f_{j}\left(\mathbf{x}_{i}\right)+\epsilon_{i},\]

其中 \(\epsilon_{i}\) 表示数据中的不确定性。最小二乘法的策略是选择系数 \(c_{j}\) 以最小化

\[ \begin{align}\begin{aligned}J\left(\mathbf{c}\right)=\sum_{i}\left|y_{i}-\sum_{j}c_{j}f_{j}\left(x_{i}\right)\right|^{2}.\\\frac{\partial J}{\partial c_{n}^{*}}=0=\sum_{i}\left(y_{i}-\sum_{j}c_{j}f_{j}\left(x_{i}\right)\right)\left(-f_{n}^{*}\left(x_{i}\right)\right)\end{aligned}\end{align} \]

或

\begin{eqnarray*} \sum_{j}c_{j}\sum_{i}f_{j}\left(x_{i}\right)f_{n}^{*}\left(x_{i}\right) & = & \sum_{i}y_{i}f_{n}^{*}\left(x_{i}\right)\\ \mathbf{A}^{H}\mathbf{Ac} & = & \mathbf{A}^{H}\mathbf{y}\end{eqnarray*},

其中

\[\left\{ \mathbf{A}\right\} _{ij}=f_{j}\left(x_{i}\right).\]

当 \(\mathbf{A^{H}A}\) 可逆时，则

\[\mathbf{c}=\left(\mathbf{A}^{H}\mathbf{A}\right)^{-1}\mathbf{A}^{H}\mathbf{y}=\mathbf{A}^{\dagger}\mathbf{y},\]

其中 \(\mathbf{A}^{\dagger}\) 被称为 \(\mathbf{A}\) 的伪逆。注意，使用这个定义的 \(\mathbf{A}\)，模型可以写成

\[\mathbf{y}=\mathbf{Ac}+\boldsymbol{\epsilon}.\]

命令 linalg.lstsq 将解决给定 \(\mathbf{A}\) 和 \(\mathbf{y}\) 的线性最小二乘问题，求解 \(\mathbf{c}\)。此外，linalg.pinv 将找到给定 \(\mathbf{A}\) 的 \(\mathbf{A}^{\dagger}\)。

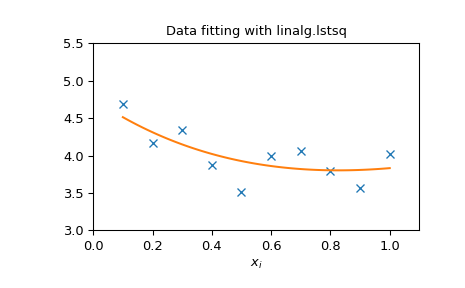
以下示例和图表展示了使用 linalg.lstsq 和 linalg.pinv 解决数据拟合问题的方法。下面显示的数据是使用以下模型生成的：

\[y_{i}=c_{1}e^{-x_{i}}+c_{2}x_{i},\]

其中 \(x_{i}=0.1i\) 对于 \(i=1\ldots10\)，\(c_{1}=5\)，以及 \(c_{2}=4\)。向 \(y_{i}\) 添加噪声，并使用线性最小二乘法估计系数 \(c_{1}\) 和 \(c_{2}\)。

>>> import numpy as np
>>> from scipy import linalg
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

>>> c1, c2 = 5.0, 2.0
>>> i = np.r_[1:11]
>>> xi = 0.1*i
>>> yi = c1*np.exp(-xi) + c2*xi
>>> zi = yi + 0.05 * np.max(yi) * rng.standard_normal(len(yi))

>>> A = np.c_[np.exp(-xi)[:, np.newaxis], xi[:, np.newaxis]]

>>> c, resid, rank, sigma = linalg.lstsq(A, zi)

>>> xi2 = np.r_[0.1:1.0:100j]
>>> yi2 = c[0]*np.exp(-xi2) + c[1]*xi2

>>> plt.plot(xi,zi,'x',xi2,yi2)
>>> plt.axis([0,1.1,3.0,5.5])
>>> plt.xlabel('$x_i$')
>>> plt.title('Data fitting with linalg.lstsq')
>>> plt.show()

广义逆#

广义逆通过命令 linalg.pinv 计算。设 \(\mathbf{A}\) 是一个 \(M\times N\) 矩阵，那么如果 \(M>N\)，广义逆为

\[\mathbf{A}^{\dagger}=\left(\mathbf{A}^{H}\mathbf{A}\right)^{-1}\mathbf{A}^{H},\]

而如果 \(M<N\) 矩阵，广义逆为

\[\mathbf{A}^{\#}=\mathbf{A}^{H}\left(\mathbf{A}\mathbf{A}^{H}\right)^{-1}.\]

在 \(M=N\) 的情况下，则

\[\mathbf{A}^{\dagger}=\mathbf{A}^{\#}=\mathbf{A}^{-1},\]

只要 \(\mathbf{A}\) 是可逆的。

分解#

在许多应用中，使用其他表示形式分解矩阵非常有用。SciPy 支持多种分解方法。

特征值和特征向量#

特征值-特征向量问题是线性代数中最常用的操作之一。在一种常见形式中，特征值-特征向量问题是为某个方阵 \(\mathbf{A}\) 找到标量 \(\lambda\) 和相应的向量 \(\mathbf{v}\)，使得

\[\mathbf{Av}=\lambda\mathbf{v}.\]

对于一个 \(N\times N\) 矩阵，存在 \(N\) 个（不一定是不同的）特征值 — 即（特征）多项式的根

\[\left|\mathbf{A}-\lambda\mathbf{I}\right|=0.\]

特征向量 \(\mathbf{v}\) 有时也称为右特征向量，以区别于另一组满足

\[\mathbf{v}_{L}^{H}\mathbf{A}=\lambda\mathbf{v}_{L}^{H}\]

或

\[\mathbf{A}^{H}\mathbf{v}_{L}=\lambda^{*}\mathbf{v}_{L}.\]

使用其默认的可选参数，命令 linalg.eig 返回 \(\lambda\) 和 \(\mathbf{v}.\) 然而，它也可以返回 \(\mathbf{v}_{L}\) 和仅 \(\lambda\) 本身（linalg.eigvals 也仅返回 \(\lambda\)）。

此外，linalg.eig 还可以解决更一般的特征值问题

\begin{eqnarray*} \mathbf{Av} & = & \lambda\mathbf{Bv}\\ \mathbf{A}^{H}\mathbf{v}_{L} & = & \lambda^{*}\mathbf{B}^{H}\mathbf{v}_{L}\end{eqnarray*}

对于方阵 \(\mathbf{A}\) 和 \(\mathbf{B}.\) 标准特征值问题是 \(\mathbf{B}=\mathbf{I}\) 时的一般特征值问题的一个例子。当一个广义特征值问题可以求解时，它提供了 \(\mathbf{A}\) 的分解为

\[\mathbf{A}=\mathbf{BV}\boldsymbol{\Lambda}\mathbf{V}^{-1},\]

其中 \(\mathbf{V}\) 是列向量形式的特征向量集合，\(\boldsymbol{\Lambda}\) 是对角矩阵形式的特征值。

根据定义，特征向量仅在常数比例因子下定义。在 SciPy 中，特征向量的比例因子选择为使得 \(\left\Vert \mathbf{v}\right\Vert ^{2}=\sum_{i}v_{i}^{2}=1.\)

作为一个例子，考虑求矩阵的特征值和特征向量

\[\begin{split}\mathbf{A}=\left[\begin{array}{ccc} 1 & 5 & 2\\ 2 & 4 & 1\\ 3 & 6 & 2\end{array}\right].\end{split}\]

其特征多项式为

\begin{eqnarray*} \left|\mathbf{A}-\lambda\mathbf{I}\right| & = & \left(1-\lambda\right)\left[\left(4-\lambda\right)\left(2-\lambda\right)-6\right]-\\ & & 5\left[2\left(2-\lambda\right)-3\right]+2\left[12-3\left(4-\lambda\right)\right]\\ & = & -\lambda^{3}+7\lambda^{2}+8\lambda-3.\end{eqnarray*}

这个多项式的根是 \(\mathbf{A}\) 的特征值：

每个特征值对应的特征向量可以通过原始方程找到。然后可以找到与这些特征值相关的特征向量。

>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1, 2], [3, 4]])
>>> la, v = linalg.eig(A)
>>> l1, l2 = la
>>> print(l1, l2)   # 特征值
(-0.3722813232690143+0j) (5.372281323269014+0j)
>>> print(v[:, 0])   # 第一个特征向量
[-0.82456484  0.56576746]
>>> print(v[:, 1])   # 第二个特征向量
[-0.41597356 -0.90937671]
>>> print(np.sum(abs(v**2), axis=0))  # 特征向量是酉的
[1. 1.]
>>> v1 = np.array(v[:, 0]).T
>>> print(linalg.norm(A.dot(v1) - l1*v1))  # 检查计算
3.23682852457e-16

奇异值分解#

奇异值分解（SVD）可以被视为对非方阵的特征值问题的扩展。设 \(\mathbf{A}\) 是一个 \(M\times N\) 矩阵，其中 \(M\) 和 \(N\) 是任意的。矩阵 \(\mathbf{A}^{H}\mathbf{A}\) 和 \(\mathbf{A}\mathbf{A}^{H}\) 分别是大小为 \(N\times N\) 和 \(M\times M\) 的厄米特矩阵 [1]。已知厄米特矩阵的特征值是实数且非负的。此外，\(\mathbf{A}^{H}\mathbf{A}\) 和 \(\mathbf{A}\mathbf{A}^{H}\) 最多有 \(\min\left(M,N\right)\) 个相同的非零特征值。将这些正特征值定义为 \(\sigma_{i}^{2}\)。这些特征值的平方根称为 \(\mathbf{A}\) 的奇异值。\(\mathbf{A}^{H}\mathbf{A}\) 的特征向量按列收集到一个 \(N\times N\) 酉矩阵 [2] \(\mathbf{V}\) 中，而 \(\mathbf{A}\mathbf{A}^{H}\) 的特征向量按列收集在酉矩阵 \(\mathbf{U}\)，奇异值被收集在一个 \(M\times N\) 的零矩阵 \(\mathbf{\boldsymbol{\Sigma}}\) 中，其主对角线元素设置为奇异值。然后

\[\mathbf{A=U}\boldsymbol{\Sigma}\mathbf{V}^{H}\]

是 \(\mathbf{A}\) 的奇异值分解。每个矩阵都有一个奇异值分解。有时，奇异值被称为 \(\mathbf{A}\) 的谱。命令 linalg.svd 将返回 \(\mathbf{U}\)、\(\mathbf{V}^{H}\) 和 \(\sigma_{i}\) 作为奇异值的数组。要获得矩阵 \(\boldsymbol{\Sigma}\)，请使用 linalg.diagsvd。以下示例说明了 linalg.svd 的使用：

>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1,2,3],[4,5,6]])
>>> A
array([[1, 2, 3],
      [4, 5, 6]])
>>> M,N = A.shape
>>> U,s,Vh = linalg.svd(A)
>>> Sig = linalg.diagsvd(s,M,N)
>>> U, Vh = U, Vh
>>> U
array([[-0.3863177 , -0.92236578],
      [-0.92236578,  0.3863177 ]])
>>> Sig
array([[ 9.508032  ,  0.        ,  0.        ],
      [ 0.        ,  0.77286964,  0.        ]])
>>> Vh
array([[-0.42866713, -0.56630692, -0.7039467 ],
      [ 0.80596391,  0.11238241, -0.58119908],
      [ 0.40824829, -0.81649658,  0.40824829]])
>>> U.dot(Sig.dot(Vh)) #检查计算
array([[ 1.,  2.,  3.],
      [ 4.,  5.,  6.]])

LU 分解#

LU 分解找到一个表示 \(M\times N\) 矩阵 \(\mathbf{A}\) 为

\[\mathbf{A}=\mathbf{P}\,\mathbf{L}\,\mathbf{U},\]

其中 \(\mathbf{P}\) 是一个 \(M\times M\) 的置换矩阵（单位矩阵的行的置换），\(\mathbf{L}\) 是一个 \(M\times K\) 的下三角或梯形矩阵（\(K=\min\left(M,N\right)\)）且对角线为单位对角线，\(\mathbf{U}\) 是一个上三角或梯形矩阵。SciPy 中用于此分解的命令是 linalg.lu。

这种分解通常对于解决许多左侧不变而右侧变化的联立方程非常有用。例如，假设我们要解决

\[\mathbf{A}\mathbf{x}_{i}=\mathbf{b}_{i}\]

对于许多不同的 \(\mathbf{b}_{i}\)。LU 分解允许将其写为

\[\mathbf{PLUx}_{i}=\mathbf{b}_{i}.\]

因为 \(\mathbf{L}\) 是下三角矩阵，方程可以快速地通过前代和回代求解 \(\mathbf{U}\mathbf{x}_{i}\) 和最终的 \(\mathbf{x}_{i}\)。初始时间用于分解 \(\mathbf{A}\) 可以在未来非常快速地解决类似的方程组。如果进行 LU 分解的目的是为了求解线性系统，那么应该使用命令 linalg.lu_factor，然后通过重复应用命令 linalg.lu_solve 来为每个新的右侧求解系统。

Cholesky 分解#

Cholesky 分解是适用于 Hermitian 正定矩阵的 LU 分解的特例。当 \(\mathbf{A}=\mathbf{A}^{H}\) 且 \(\mathbf{x}^{H}\mathbf{Ax}\geq0\) 对于所有 \(\mathbf{x}\) 成立时，可以找到 \(\mathbf{A}\) 的分解，使得

\begin{eqnarray*} \mathbf{A} & = & \mathbf{U}^{H}\mathbf{U}\\ \mathbf{A} & = & \mathbf{L}\mathbf{L}^{H}\end{eqnarray*},

其中 \(\mathbf{L}\) 是下三角矩阵，\(\mathbf{U}\) 是上三角矩阵。注意 \(\mathbf{L}=\mathbf{U}^{H}.\) 命令 linalg.cholesky 计算 Cholesky 分解。为了使用 Cholesky 分解来求解方程组，还有 linalg.cho_factor 和 linalg.cho_solve 例程，它们的工作方式类似于它们的 LU 分解对应部分。

QR 分解#

QR 分解（有时称为极分解）适用于任何 \(M\times N\) 数组，并找到一个 \(M\times M\) 的酉矩阵 \(\mathbf{Q}\) 和一个 \(M\times N\) 的上梯形矩阵 \(\mathbf{R}\)，使得

\[\mathbf{A=QR}.\]

请注意，如果已知 \(\mathbf{A}\) 的 SVD，则可以找到 QR 分解。

\[\mathbf{A}=\mathbf{U}\boldsymbol{\Sigma}\mathbf{V}^{H}=\mathbf{QR}\]

这意味着 \(\mathbf{Q}=\mathbf{U}\) 和 \(\mathbf{R}=\boldsymbol{\Sigma}\mathbf{V}^{H}\)。然而，请注意，在 SciPy 中，QR 分解和 SVD 分解使用独立的算法。QR 分解的命令是 linalg.qr。

Schur 分解#

对于一个方形的 \(N\times N\) 矩阵 \(\mathbf{A}\)，Schur 分解找到（不一定是唯一的）矩阵 \(\mathbf{T}\) 和 \(\mathbf{Z}\)，使得

\[\mathbf{A}=\mathbf{ZT}\mathbf{Z}^{H},\]

其中 \(\mathbf{Z}\) 是酉矩阵，而 \(\mathbf{T}\) 是上三角矩阵或准上三角矩阵，具体取决于是否请求了实 Schur 形式或复 Schur 形式。对于实 Schur 形式，当 \(\mathbf{A}\) 是实值矩阵时，\(\mathbf{T}\) 和 \(\mathbf{Z}\) 都是实值的。当 \(\mathbf{A}\) 是实值矩阵时，实 Schur 形式仅是准上三角的，因为对应于任何复值特征值的 \(2\times2\) 块会从主对角线上突出。命令 linalg.schur 找到 Schur 分解，而命令 linalg.rsf2csf 转换 \(\mathbf{T}\) 和 \(\mathbf{Z}\) 从实 Schur 形式转换为复 Schur 形式。Schur 形式在计算矩阵函数时特别有用。

以下示例说明了 Schur 分解：

>>> from scipy import linalg
>>> A = np.asmatrix('[1 3 2; 1 4 5; 2 3 6]')
>>> T, Z = linalg.schur(A)
>>> T1, Z1 = linalg.schur(A, 'complex')
>>> T2, Z2 = linalg.rsf2csf(T, Z)
>>> T
array([[ 9.90012467,  1.78947961, -0.65498528],
       [ 0.        ,  0.54993766, -1.57754789],
       [ 0.        ,  0.51260928,  0.54993766]])
>>> T2
array([[ 9.90012467+0.00000000e+00j, -0.32436598+1.55463542e+00j,
        -0.88619748+5.69027615e-01j],
       [ 0.        +0.00000000e+00j,  0.54993766+8.99258408e-01j,
         1.06493862+3.05311332e-16j],
       [ 0.        +0.00000000e+00j,  0.        +0.00000000e+00j,
         0.54993766-8.99258408e-01j]])
>>> abs(T1 - T2) # 不同
array([[  1.06604538e-14,   2.06969555e+00,   1.69375747e+00],  # 可能会有所不同
       [  0.00000000e+00,   1.33688556e-15,   4.74146496e-01],
       [  0.00000000e+00,   0.00000000e+00,   1.13220977e-15]])
>>> abs(Z1 - Z2) # 不同
array([[ 0.06833781,  0.88091091,  0.79568503],    # 可能会有所不同
       [ 0.11857169,  0.44491892,  0.99594171],
       [ 0.12624999,  0.60264117,  0.77257633]])
>>> T, Z, T1, Z1, T2, Z2 = map(np.asmatrix,(T,Z,T1,Z1,T2,Z2))
>>> abs(A - Z*T*Z.H)  # 相同
matrix([[  5.55111512e-16,   1.77635684e-15,   2.22044605e-15],
        [  0.00000000e+00,   3.99680289e-15,   8.88178420e-16],
        [  1.11022302e-15,   4.44089210e-16,   3.55271368e-15]])
>>> abs(A - Z1*T1*Z1.H)  # 相同
matrix([[  4.26993904e-15,   6.21793362e-15,   8.00007092e-15],
        [  5.77945386e-15,   6.21798014e-15,   1.06653681e-14],
        [  7.16681444e-15,   8.90271058e-15,   1.77635764e-14]])
>>> abs(A - Z2*T2*Z2.H)  # 相同

matrix([[ 6.02594127e-16, 1.77648931e-15, 2.22506907e-15],: [ 2.46275555e-16, 3.99684548e-15, 8.91642616e-16], [ 8.88225111e-16, 8.88312432e-16, 4.44104848e-15]])

插值分解#

scipy.linalg.interpolative 包含计算矩阵插值分解（ID）的例程。对于秩为 \(k \leq \min \{ m, n \}\) 的矩阵 \(A \in \mathbb{C}^{m \times n}\)，这是一个分解

\[A \Pi = \begin{bmatrix} A \Pi_{1} & A \Pi_{2} \end{bmatrix} = A \Pi_{1} \begin{bmatrix} I & T \end{bmatrix},\]

其中 \(\Pi = [\Pi_{1}, \Pi_{2}]\) 是一个置换矩阵，且 \(\Pi_{1} \in \{ 0, 1 \}^{n \times k}\)，即 \(A \Pi_{2} = A \Pi_{1} T\)。这可以等价地写成 \(A = BP\)，其中 \(B = A \Pi_{1}\) 和 \(P = [I, T] \Pi^{\mathsf{T}}\) 分别是 骨架矩阵 和 插值矩阵。

参见

scipy.linalg.interpolative — 了解更多信息。

矩阵函数#

考虑函数 \(f\left(x\right)\) 的泰勒级数展开

\[f\left(x\right)=\sum_{k=0}^{\infty}\frac{f^{\left(k\right)}\left(0\right)}{k!}x^{k}.\]

可以使用这个泰勒级数来定义方阵 \(\mathbf{A}\) 的矩阵函数

\[f\left(\mathbf{A}\right)=\sum_{k=0}^{\infty}\frac{f^{\left(k\right)}\left(0\right)}{k!}\mathbf{A}^{k}.\]

备注

虽然这为矩阵函数提供了一个有用的表示，但它很少是计算矩阵函数的最佳方法。特别是，如果矩阵不可对角化，结果可能不准确。

指数和对数函数#

矩阵指数是更常见的矩阵函数之一。实现矩阵指数的首选方法是使用缩放和 Padé 近似法来计算 \(e^{x}\)。该算法是实现为 linalg.expm。

矩阵指数的逆是矩阵对数，定义为矩阵指数的逆：

\[\mathbf{A}\equiv\exp\left(\log\left(\mathbf{A}\right)\right).\]

矩阵对数可以通过 linalg.logm 获得。

三角函数#

三角函数 \(\sin\)、\(\cos\) 和 \(\tan\) 分别在 linalg.sinm、linalg.cosm 和 linalg.tanm 中为矩阵实现。矩阵的正弦和余弦可以使用欧拉公式定义为

\begin{eqnarray*} \sin\left(\mathbf{A}\right) & = & \frac{e^{j\mathbf{A}}-e^{-j\mathbf{A}}}{2j}\\ \cos\left(\mathbf{A}\right) & = & \frac{e^{j\mathbf{A}}+e^{-j\mathbf{A}}}{2}.\end{eqnarray*}

正切为

\[\tan\left(x\right)=\frac{\sin\left(x\right)}{\cos\left(x\right)}=\left[\cos\left(x\right)\right]^{-1}\sin\left(x\right)\]

因此，矩阵正切定义为

\[\left[\cos\left(\mathbf{A}\right)\right]^{-1}\sin\left(\mathbf{A}\right).\]

命令 linalg.funm。该命令接受一个矩阵和一个任意的Python函数。然后，它实现了一个来自Golub和Van Loan的著作《矩阵计算》中的算法，通过Schur分解来计算应用于矩阵的函数。请注意，*该函数需要接受复数*作为输入，以便与此算法一起使用。例如，以下代码计算应用于矩阵的零阶贝塞尔函数。

>>> from scipy import special, linalg
>>> rng = np.random.default_rng()
>>> A = rng.random((3, 3))
>>> B = linalg.funm(A, lambda x: special.jv(0, x))
>>> A
array([[0.06369197, 0.90647174, 0.98024544],
       [0.68752227, 0.5604377 , 0.49142032],
       [0.86754578, 0.9746787 , 0.37932682]])
>>> B
array([[ 0.6929219 , -0.29728805, -0.15930896],
       [-0.16226043,  0.71967826, -0.22709386],
       [-0.19945564, -0.33379957,  0.70259022]])
>>> linalg.eigvals(A)
array([ 1.94835336+0.j, -0.72219681+0.j, -0.22270006+0.j])
>>> special.jv(0, linalg.eigvals(A))
array([0.25375345+0.j, 0.87379738+0.j, 0.98763955+0.j])
>>> linalg.eigvals(B)
array([0.25375345+0.j, 0.87379738+0.j, 0.98763955+0.j])

请注意，由于矩阵解析函数的定义方式，贝塞尔函数是如何作用于矩阵特征值的。

特殊矩阵#

SciPy和NumPy提供了几个用于创建工程和科学中常用的特殊矩阵的函数。

类型	函数	描述
块对角矩阵	`scipy.linalg.block_diag`	从提供的数组创建一个块对角矩阵。
circulant	`scipy.linalg.circulant`	创建一个循环矩阵。
companion	`scipy.linalg.companion`	创建一个伴随矩阵。
convolution	`scipy.linalg.convolution_matrix`	创建一个卷积矩阵。
Discrete Fourier	`scipy.linalg.dft`	创建一个离散傅里叶变换矩阵。
Fiedler	`scipy.linalg.fiedler`	创建一个对称Fiedler矩阵。
Fiedler Companion	`scipy.linalg.fiedler_companion`	创建一个Fiedler伴随矩阵。
Hadamard	`scipy.linalg.hadamard`	创建一个Hadamard矩阵。
Hankel	`scipy.linalg.hankel`	创建一个Hankel矩阵。
Helmert	`scipy.linalg.helmert`	创建一个Helmert矩阵。
Hilbert	`scipy.linalg.hilbert`	创建一个希尔伯特矩阵。
Inverse Hilbert	`scipy.linalg.invhilbert`	创建希尔伯特矩阵的逆矩阵。
Leslie	`scipy.linalg.leslie`	创建一个莱斯利矩阵。
Pascal	`scipy.linalg.pascal`	创建一个帕斯卡矩阵。
Inverse Pascal	`scipy.linalg.invpascal`	创建帕斯卡矩阵的逆矩阵。
Toeplitz	`scipy.linalg.toeplitz`	创建一个Toeplitz矩阵。
Van der Monde	`numpy.vander`	创建一个范德蒙矩阵。

有关这些函数的使用示例，请参阅它们各自的文档字符串。

线性代数 (scipy.linalg)#