分段多项式与样条#
一维插值例程 在上一节中讨论过,通过构建某些 分段多项式 来工作:插值范围由所谓的 断点 分割成区间,每个区间上有一个特定的多项式。这些多项式片段在断点处根据预定义的平滑度匹配:三次样条的二阶导数,单调插值的一阶导数等等。
一个次数为 \(k\) 的多项式可以被认为是 \(k+1\) 个单项基元素 \(1, x, x^2, \cdots, x^k\) 的线性组合。在某些应用中,考虑替代的(形式上等价的)基是有用的。scipy.interpolate 中实现了两种流行的基:B样条 (BSpline) 和 Bernstein 多项式 (BPoly)。B样条常用于非参数回归问题,而 Bernstein 多项式用于构造 Bezier 曲线。
PPoly 对象表示以“通常”幂基表示的分段多项式。这是 CubicSpline 实例和单调插值的情况。一般来说,PPoly 对象可以表示任意次数的多项式,不仅仅是三次多项式。对于数据数组 x,断点位于数据点处,系数数组 c 定义了次数为 \(k\) 的多项式,使得 c[i, j] 是 (x - x[j])**(k-i) 在 x[j] 和 x[j+1] 之间的区段上的系数。
BSpline 对象表示 B 样条函数—— B 样条基元素 的线性组合。这些对象可以直接实例化,也可以通过 make_interp_spline 工厂函数从数据构造。
最后,Bernstein 多项式表示为 BPoly 类的实例。
所有这些类实现了一个(大部分)相似的接口,PPoly 是最为功能完善的。接下来,我们将考虑这个接口的主要特性,并讨论分段多项式的替代基底的一些细节。
操作 PPoly 对象#
PPoly 对象具有方便的方法来构造导数和原函数,计算积分和求根。例如,我们列出正弦函数的值并找到其导数的根。
>>> import numpy as np
>>> from scipy.interpolate import CubicSpline
>>> x = np.linspace(0, 10, 71)
>>> y = np.sin(x)
>>> spl = CubicSpline(x, y)
现在,对样条进行求导:
>>> dspl = spl.derivative()
这里 dspl 是一个 PPoly 实例,表示对原始对象 spl 的导数的近似多项式。在固定参数处评估 dspl 等同于使用 nu=1 参数评估原始样条:
>>> dspl(1.1), spl(1.1, nu=1)
(0.45361436, 0.45361436)
注意,上面的第二种形式在原地评估导数,而使用 dspl 对象,我们可以找到 spl 导数的零点:
>>> dspl.roots() / np.pi
array([-0.45480801, 0.50000034, 1.50000099, 2.5000016 , 3.46249993])
这与 \(\cos(x) = \sin'(x)\) 的根 \(\pi/2 + \pi\,n\) 吻合良好。 注意,默认情况下,它计算了插值区间 \(0 \leqslant x \leqslant 10\) 之外的*外推*根,并且外推结果(第一个和最后一个值)的精度较低。 我们可以关闭外推,并将求根限制在插值区间内:
>>> dspl.roots(extrapolate=False) / np.pi
array([0.50000034, 1.50000099, 2.5000016])
事实上,root 方法是更一般的 solve 方法的一个特例,该方法为给定的常数 \(y\) 找到方程的解。
方程 \(f(x) = y\) ,其中 \(f(x)\) 是分段多项式:
>>> dspl.solve(0.5, extrapolate=False) / np.pi
array([0.33332755, 1.66667195, 2.3333271])
这与预期的值 \(\pm\arccos(1/2) + 2\pi\,n\) 非常吻合。
分段多项式的积分可以使用 .integrate 方法计算,该方法接受积分的下限和上限。作为一个例子,我们计算完全椭圆积分 \(K(m) = \int_0^{\pi/2} [1 - m\sin^2 x]^{-1/2} dx\) 的近似值:
>>> from scipy.special import ellipk
>>> m = 0.5
>>> ellipk(m)
1.8540746773013719
为此,我们制表被积函数并用单调 PCHIP 插值器对其进行插值(我们也可以使用 CubicSpline):
>>> from scipy.interpolate import PchipInterpolator
>>> x = np.linspace(0, np.pi/2, 70)
>>> y = (1 - m*np.sin(x)**2)**(-1/2)
>>> spl = PchipInterpolator(x, y)
并进行积分
>>> spl.integrate(0, np.pi/2)
1.854074674965991
这确实接近于 scipy.special.ellipk 计算的值。
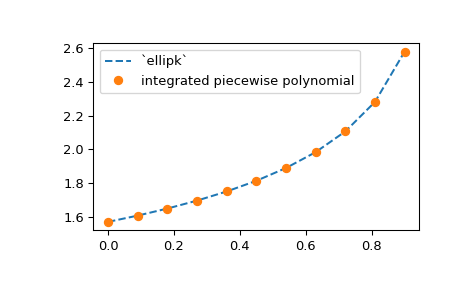
所有分段多项式都可以用 N 维的 y 值构建。如果 y.ndim > 1,则将其理解为沿插值轴(默认值为 0)排列的 1D y 值的堆栈。后者通过 axis 参数指定,并且不变量是 len(x) == y.shape[axis]。作为一个例子,我们将上面的椭圆积分示例扩展到计算一系列 m 值的近似值,使用 NumPy 广播:
>>> from scipy.interpolate import PchipInterpolator
>>> m = np.linspace(0, 0.9, 11)
>>> x = np.linspace(0, np.pi/2, 70)
>>> y = 1 / np.sqrt(1 - m[:, None]*np.sin(x)**2)
现在 y 数组的形状为 (11, 70),因此对于固定的 m 值,y 的值沿 y 数组的第二轴排列。
>>> spl = PchipInterpolator(x, y, axis=1) # 默认是 axis=0
>>> import matplotlib.pyplot as plt
>>> plt.plot(m, spl.integrate(0, np.pi/2), '--')
>>> from scipy.special import ellipk
>>> plt.plot(m, ellipk(m), 'o')
>>> plt.legend(['`ellipk`', 'integrated piecewise polynomial'])
>>> plt.show()
B样条:节点与系数#
一个B样条函数——例如,通过`make_interp_spline`调用从数据构建的——由所谓的*节点*和系数定义。
为了说明这一点,让我们再次构建一个正弦函数的插值。节点可以通过`BSpline`实例的``t``属性获得:
>>> x = np.linspace(0, 3/2, 7)
>>> y = np.sin(np.pi*x)
>>> from scipy.interpolate import make_interp_spline
>>> bspl = make_interp_spline(x, y, k=3)
>>> print(bspl.t)
[0. 0. 0. 0. 0.5 0.75 1. 1.5 1.5 1.5 1.5 ]
>>> print(x)
[ 0. 0.25 0.5 0.75 1. 1.25 1.5 ]
我们看到,节点向量默认是从输入数组``x``构建的:首先,它被制成:math:(k+1)-正则(在开头和结尾附加了``k``个重复的节点);然后,输入数组的第二个和倒数第二个点被移除——这就是所谓的*非节点*边界条件。
一般来说,一个度数为``k``的插值样条需要``len(t) - len(x) - k - 1``个边界条件。对于具有``(k+1)``-正则节点数组的立方样条,这意味着两个边界条件——或者从``x``数组中移除两个值。可以使用`make_interp_spline`的可选``bc_type``参数请求各种边界条件。
B样条系数通过`BSpline`对象的``c``属性访问:
>>> len(bspl.c)
7
约定是对于``len(t)``个节点有``len(t) - k - 1``个系数。一些例程(参见:ref:平滑样条部分)会将``c``数组零填充,以便
len(c) == len(t). 这些额外的系数在评估时会被忽略。
我们强调,这些系数是以 B样条基 给出的,而不是以 \(1, x, \cdots, x^k\) 的幂基给出的。
B样条基元素#
B样条是分段多项式,表示为 B样条基元素 的线性组合——这些基元素本身是某些通常的单项式 \(x^m\) (其中 \(m=0, 1, \dots, k\))的线性组合。
B样条基通常比幂基在计算上更稳定,并且对于包括插值、回归和曲线表示在内的各种应用都很有用。其主要特点是这些基元素是 局部的,并且在由 节点数组 定义的区间之外等于零。
具体来说,一个度数为 k 的B样条基元素(例如,对于三次样条,k=3)由 \(k+2\) 个节点定义,并且在这些节点之外为零。为了说明,在一个特定区间上绘制一组非零基元素:
>>> k = 3 # 三次样条
>>> t = [0., 1.4, 2., 3.1, 5.] # 内部节点
>>> t = np.r_[[0]*k, t, [5]*k] # 添加边界节点
>>> from scipy.interpolate import BSpline
>>> import matplotlib.pyplot as plt
>>> for j in [-2, -1, 0, 1, 2]:
... a, b = t[k+j], t[-k+j-1]
... xx = np.linspace(a, b, 101)
... bspl = BSpline.basis_element(t[k+j:-k+j])
... plt.plot(xx, bspl(xx), label=f'j = {j}')
>>> plt.legend(loc='best')
>>> plt.show()
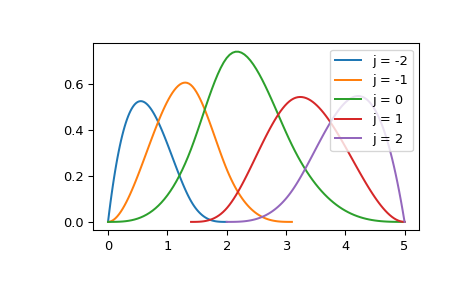
这里 BSpline.basis_element 本质上是一个简写,用于构造只有一个非零系数的样条。例如,上面例子中的 j=2 元素等价于
>>> c = np.zeros(t.size - k - 1)
>>> c[-2] = 1
>>> b = BSpline(t, c, k)
>>> np.allclose(b(xx), bspl(xx))
True
如果需要,可以使用 PPoly.from_spline 方法将 b-spline 转换为 PPoly 对象,该方法接受一个 BSpline 实例并返回一个 PPoly 实例。反向转换则由 BSpline.from_power_basis 方法执行。然而,最好避免在基之间进行转换,因为这会累积舍入误差。
B-spline 基中的设计矩阵#
b-spline 的一个常见应用是非参数回归。其原因是 b-spline 基元素的局部性质使得线性代数具有带状结构。这是因为在一个给定的评估点上,最多有 \(k+1\) 个基元素是非零的,因此基于 b-spline 构建的设计矩阵最多有 \(k+1\) 个对角线。
作为说明,我们考虑一个简单的例子。假设我们的数据是一维的,并且限定在区间 \([0, 6]\) 内。我们构造一个 4-regular 的节点向量,对应于 7 个数据点和三次(k=3)样条:
>>> t = [0., 0., 0., 0., 2., 3., 4., 6., 6., 6., 6.]
接下来,取 ‘观测值’ 为
>>> xnew = [1, 2, 3]
并在稀疏 CSR 格式中构造设计矩阵
>>> from scipy.interpolate import BSpline
>>> mat = BSpline.design_matrix(xnew, t, k=3)
>>> mat
<Compressed Sparse Row sparse array of dtype 'float64'
with 12 stored elements and shape (3, 7)>
这里,设计矩阵的每一行对应于 xnew 数组中的一个值,并且一行最多有 k+1 = 4 个非零元素;第 j 行包含在 xnew[j] 处评估的基元素:
>>> with np.printoptions(precision=3):
... print(mat.toarray())
[[0.125 0.514 0.319 0.042 0. 0. 0. ]
[0. 0.111 0.556 0.333 0. 0. 0. ]
[0. 0. 0.125 0.75 0.125 0. 0. ]]