%%capture
!pip install hierarchicalforecast statsforecast引导程序
在许多情况下,只有层次结构中最低级别的时间序列(底层时间序列)可用。 HierarchicalForecast 提供了创建所有层次结构时间序列的工具,并允许你计算所有层次结构的预测区间。在本笔记本中,我们将看看如何做到这一点。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 计算基础预测无连贯性
from statsforecast.models import ETS, Naive
from statsforecast.core import StatsForecast
#获取层次协调方法及评估
from hierarchicalforecast.methods import BottomUp, MinTrace
from hierarchicalforecast.utils import aggregate, HierarchicalPlot
from hierarchicalforecast.core import HierarchicalReconciliation
from hierarchicalforecast.evaluation import HierarchicalEvaluation/Users/fedex/miniconda3/envs/hierarchicalforecast/lib/python3.10/site-packages/statsforecast/core.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
from tqdm.autonotebook import tqdm汇总底部时间序列
在这个示例中,我们将使用来自《预测:原理与实践》一书的旅游数据集。该数据集仅包含最低层级的时间序列,因此我们需要为所有层级创建时间序列。
Y_df = pd.read_csv('https://raw.githubusercontent.com/Nixtla/transfer-learning-time-series/main/datasets/tourism.csv')
Y_df = Y_df.rename({'Trips': 'y', 'Quarter': 'ds'}, axis=1)
Y_df.insert(0, 'Country', 'Australia')
Y_df = Y_df[['Country', 'Region', 'State', 'Purpose', 'ds', 'y']]
Y_df['ds'] = Y_df['ds'].str.replace(r'(\d+) (Q\d)', r'\1-\2', regex=True)
Y_df['ds'] = pd.to_datetime(Y_df['ds'])
Y_df.head()| Country | Region | State | Purpose | ds | y | |
|---|---|---|---|---|---|---|
| 0 | Australia | Adelaide | South Australia | Business | 1998-01-01 | 135.077690 |
| 1 | Australia | Adelaide | South Australia | Business | 1998-04-01 | 109.987316 |
| 2 | Australia | Adelaide | South Australia | Business | 1998-07-01 | 166.034687 |
| 3 | Australia | Adelaide | South Australia | Business | 1998-10-01 | 127.160464 |
| 4 | Australia | Adelaide | South Australia | Business | 1999-01-01 | 137.448533 |
数据集可以在以下非严格层次结构中进行分组。
spec = [
['Country'],
['Country', 'State'],
['Country', 'Purpose'],
['Country', 'State', 'Region'],
['Country', 'State', 'Purpose'],
['Country', 'State', 'Region', 'Purpose']
]使用HierarchicalForecast中的aggregate函数,我们可以生成: 1. Y_df: 层次结构化的序列 \(\mathbf{y}_{[a,b]\tau}\) 2. S_df: 具有 \(S_{[a,b]}\) 的聚合约束数据框 3. tags: 一个包含每个聚合级别的’unique_ids’的列表。
Y_df, S_df, tags = aggregate(df=Y_df, spec=spec)
Y_df = Y_df.reset_index()/Users/fedex/miniconda3/envs/hierarchicalforecast/lib/python3.10/site-packages/sklearn/preprocessing/_encoders.py:828: FutureWarning: `sparse` was renamed to `sparse_output` in version 1.2 and will be removed in 1.4. `sparse_output` is ignored unless you leave `sparse` to its default value.
warnings.warn(Y_df.head()| unique_id | ds | y | |
|---|---|---|---|
| 0 | Australia | 1998-01-01 | 23182.197269 |
| 1 | Australia | 1998-04-01 | 20323.380067 |
| 2 | Australia | 1998-07-01 | 19826.640511 |
| 3 | Australia | 1998-10-01 | 20830.129891 |
| 4 | Australia | 1999-01-01 | 22087.353380 |
S_df.iloc[:5, :5]| Australia/ACT/Canberra/Business | Australia/ACT/Canberra/Holiday | Australia/ACT/Canberra/Other | Australia/ACT/Canberra/Visiting | Australia/New South Wales/Blue Mountains/Business | |
|---|---|---|---|---|---|
| Australia | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Australia/ACT | 1.0 | 1.0 | 1.0 | 1.0 | 0.0 |
| Australia/New South Wales | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| Australia/Northern Territory | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Australia/Queensland | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
tags['Country/Purpose']array(['Australia/Business', 'Australia/Holiday', 'Australia/Other',
'Australia/Visiting'], dtype=object)我们可以使用 HierarchicalPlot 类可视化 S_df 数据框和 Y_df,具体如下。
hplot = HierarchicalPlot(S=S_df, tags=tags)hplot.plot_summing_matrix()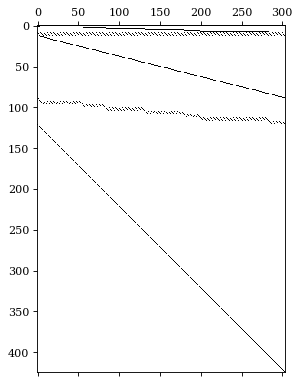
hplot.plot_hierarchically_linked_series(
bottom_series='Australia/ACT/Canberra/Holiday',
Y_df=Y_df.set_index('unique_id')
)
切分训练/测试集
我们使用最后两年(8个季度)作为测试集。
Y_test_df = Y_df.groupby('unique_id').tail(8)
Y_train_df = Y_df.drop(Y_test_df.index)Y_test_df = Y_test_df.set_index('unique_id')
Y_train_df = Y_train_df.set_index('unique_id')Y_train_df.groupby('unique_id').size()unique_id
Australia 72
Australia/ACT 72
Australia/ACT/Business 72
Australia/ACT/Canberra 72
Australia/ACT/Canberra/Business 72
..
Australia/Western Australia/Experience Perth/Other 72
Australia/Western Australia/Experience Perth/Visiting 72
Australia/Western Australia/Holiday 72
Australia/Western Australia/Other 72
Australia/Western Australia/Visiting 72
Length: 425, dtype: int64计算基础预测
以下单元格使用 AutoETS 模型计算 Y_df 中每个时间序列的 基础预测。请注意,Y_hat_df 包含预测值,但它们并不一致。由于我们使用自助法计算预测区间,因此我们只需要模型的拟合值。
fcst = StatsForecast(df=Y_train_df,
models=[ETS(season_length=4, model='ZAA')],
freq='QS', n_jobs=-1)
Y_hat_df = fcst.forecast(h=8, fitted=True)
Y_fitted_df = fcst.forecast_fitted_values()/Users/fedex/miniconda3/envs/hierarchicalforecast/lib/python3.10/site-packages/statsforecast/models.py:526: FutureWarning: `ETS` will be deprecated in future versions of `StatsForecast`. Please use `AutoETS` instead.
ETS._warn()调和基础预测
以下单元使用 HierarchicalReconciliation 类使之前的预测结果一致。由于层次结构并不严格,我们无法使用 TopDown 或 MiddleOut 等方法。在这个例子中,我们使用 BottomUp 和 MinTrace。如果您想计算预测区间,则必须使用 level 参数,如下所示,并将 intervals_method 设置为 'bootstrap'。
reconcilers = [
BottomUp(),
MinTrace(method='mint_shrink'),
MinTrace(method='ols')
]
hrec = HierarchicalReconciliation(reconcilers=reconcilers)
Y_rec_df = hrec.reconcile(Y_hat_df=Y_hat_df, Y_df=Y_fitted_df, S=S_df,
tags=tags, level=[80, 90],
intervals_method='bootstrap')数据框 Y_rec_df 包含已调和的预测数据。
Y_rec_df.head()| ds | ETS | ETS/BottomUp | ETS/BottomUp-lo-90 | ETS/BottomUp-lo-80 | ETS/BottomUp-hi-80 | ETS/BottomUp-hi-90 | ETS/MinTrace_method-mint_shrink | ETS/MinTrace_method-mint_shrink-lo-90 | ETS/MinTrace_method-mint_shrink-lo-80 | ETS/MinTrace_method-mint_shrink-hi-80 | ETS/MinTrace_method-mint_shrink-hi-90 | ETS/MinTrace_method-ols | ETS/MinTrace_method-ols-lo-90 | ETS/MinTrace_method-ols-lo-80 | ETS/MinTrace_method-ols-hi-80 | ETS/MinTrace_method-ols-hi-90 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| unique_id | |||||||||||||||||
| Australia | 2016-01-01 | 26080.878906 | 24487.349609 | 23244.120996 | 23333.694727 | 25381.792969 | 25426.333984 | 25532.523559 | 24428.911701 | 24709.210638 | 26365.606934 | 26476.255501 | 26034.114241 | 24914.136375 | 25100.462938 | 27102.735022 | 27176.416922 |
| Australia | 2016-04-01 | 24587.011719 | 23069.744141 | 21826.519434 | 21912.962891 | 23946.606250 | 24281.447266 | 24118.557177 | 23199.968626 | 23295.244252 | 25108.470410 | 25489.383606 | 24567.460995 | 23484.050568 | 23640.638423 | 25709.763678 | 25809.249492 |
| Australia | 2016-07-01 | 24147.308594 | 22689.777344 | 21297.136719 | 21530.438281 | 23701.173828 | 24155.820312 | 23731.251387 | 22627.639669 | 22818.729182 | 24821.488458 | 25246.867432 | 24150.134898 | 23030.156834 | 23155.025556 | 25359.992376 | 25404.841402 |
| Australia | 2016-10-01 | 24794.041016 | 23429.757812 | 22037.123047 | 22276.453125 | 24241.417969 | 24441.160156 | 24486.549344 | 23385.927232 | 23600.704525 | 25353.555625 | 25481.478557 | 24831.584516 | 23725.924464 | 23836.475174 | 25900.205254 | 25977.265089 |
| Australia | 2017-01-01 | 26284.000000 | 24940.042969 | 23696.722754 | 23904.382812 | 25814.941406 | 25974.169922 | 26041.867488 | 24972.077858 | 25158.986710 | 26918.104747 | 27135.580845 | 26348.203335 | 25254.659324 | 25487.502291 | 27410.873035 | 27477.334507 |
绘制预测结果
然后我们可以使用以下函数绘制概率预测。
plot_df = pd.concat([Y_df.set_index(['unique_id', 'ds']),
Y_rec_df.set_index('ds', append=True)], axis=1)
plot_df = plot_df.reset_index('ds')绘制单个时间序列
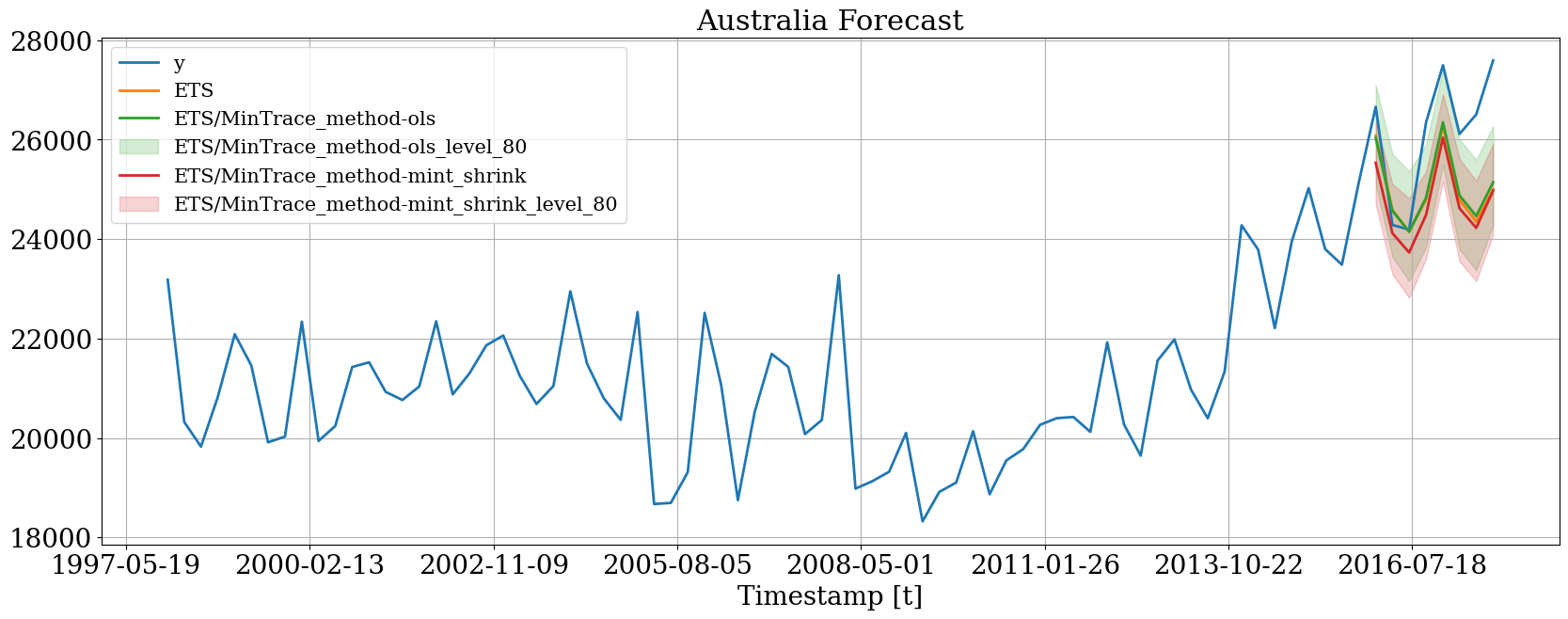
hplot.plot_series(
series='Australia',
Y_df=plot_df,
models=['y', 'ETS', 'ETS/MinTrace_method-ols', 'ETS/MinTrace_method-mint_shrink'],
level=[80]
)
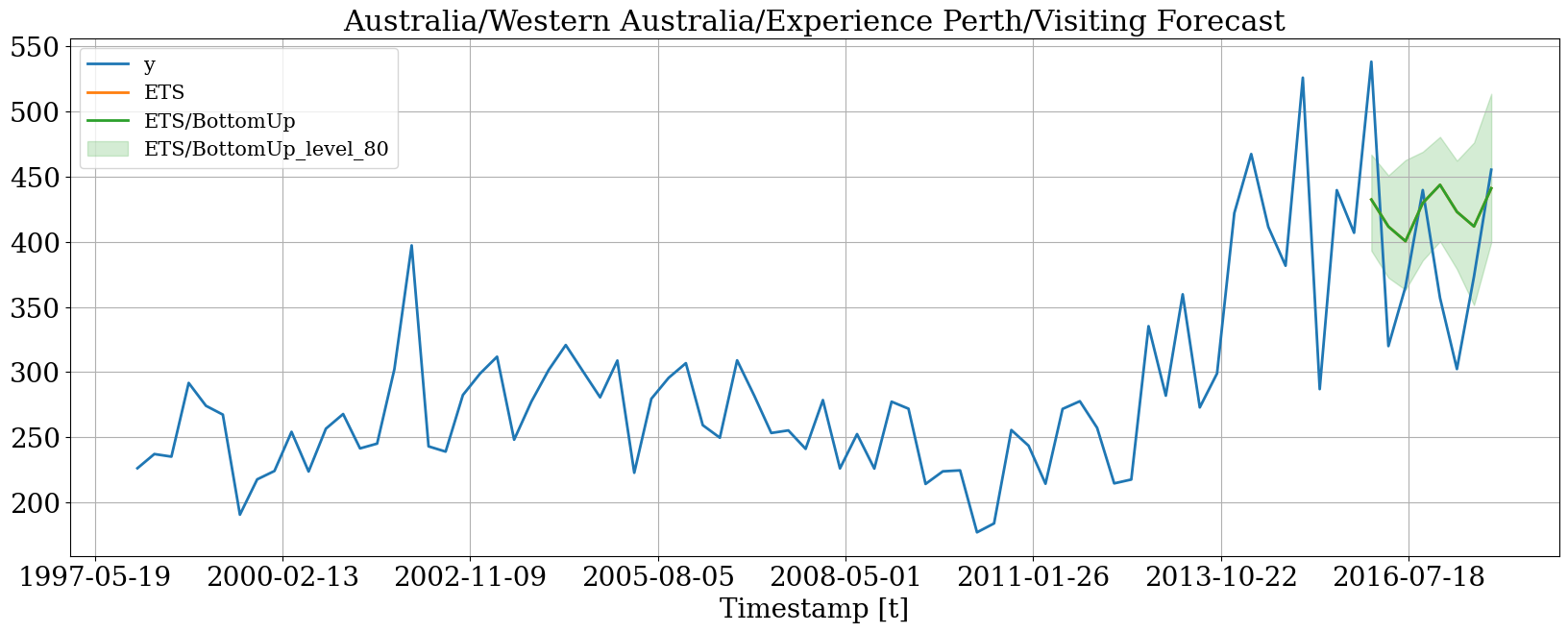
# 由于我们正在绘制一个底部时间序列
# 概率预报和平均预报
# 由于自举而有所不同
hplot.plot_series(
series='Australia/Western Australia/Experience Perth/Visiting',
Y_df=plot_df,
models=['y', 'ETS', 'ETS/BottomUp'],
level=[80]
)
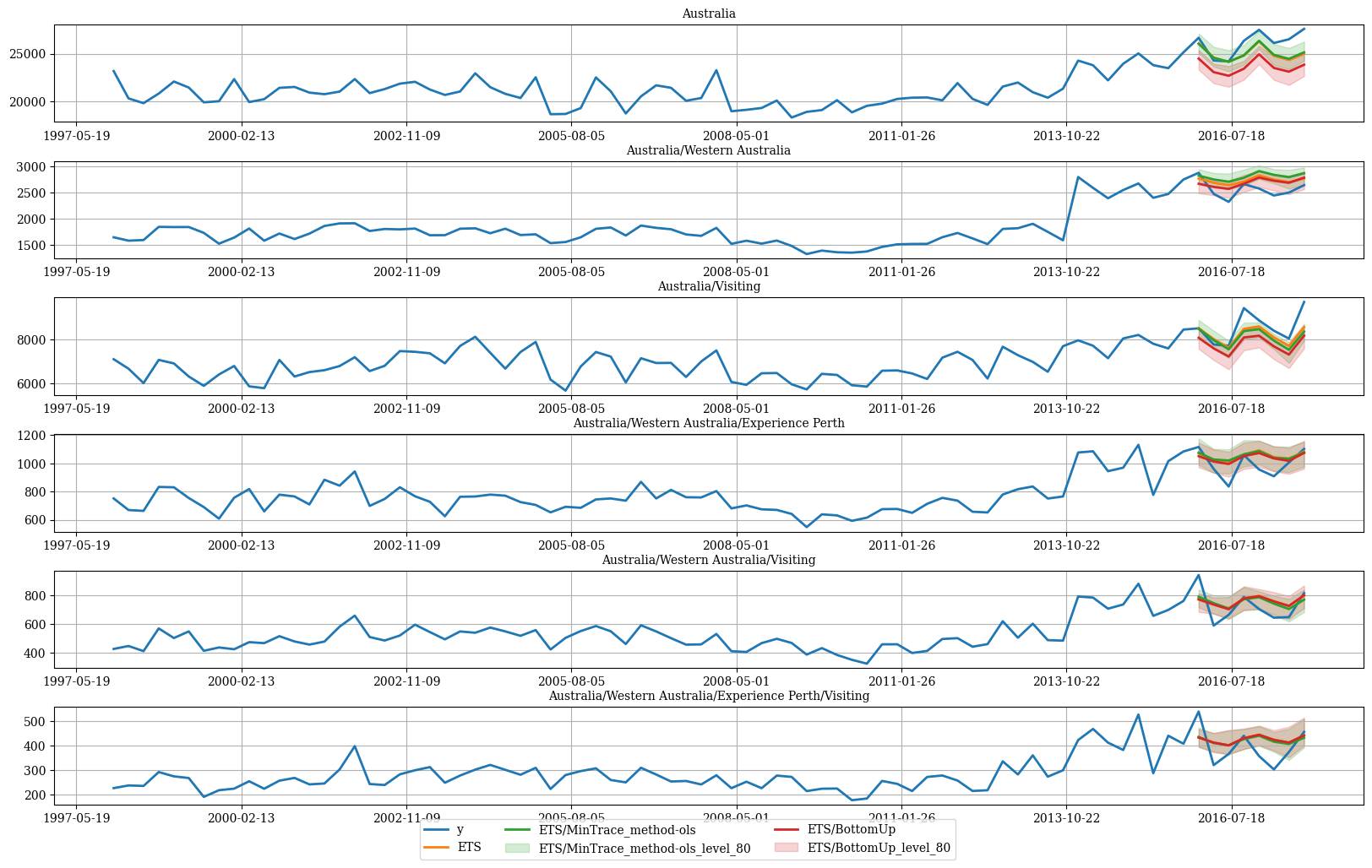
绘制层级关联时间序列
hplot.plot_hierarchically_linked_series(
bottom_series='Australia/Western Australia/Experience Perth/Visiting',
Y_df=plot_df,
models=['y', 'ETS', 'ETS/MinTrace_method-ols', 'ETS/BottomUp'],
level=[80]
)
# ACT仅包括堪培拉
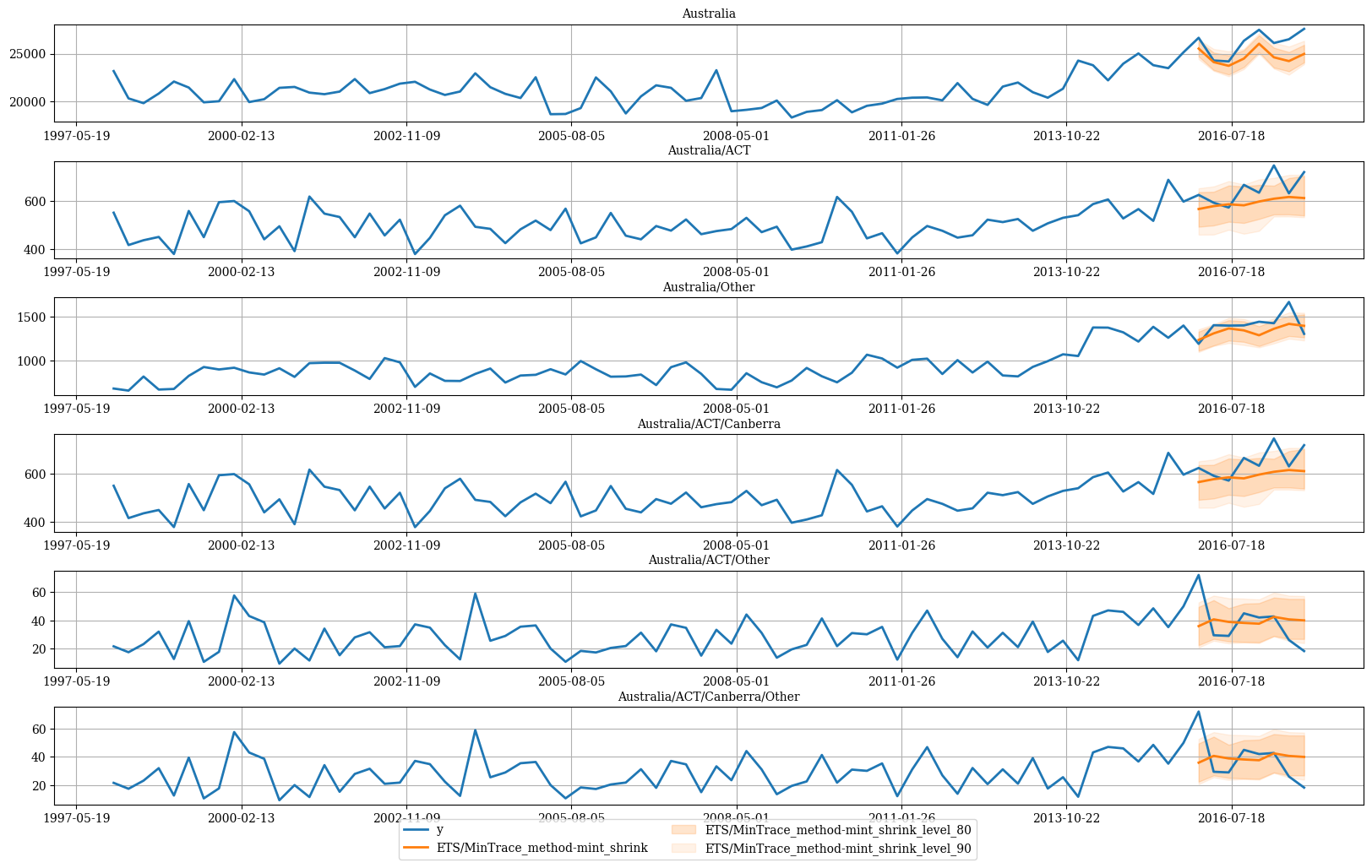
hplot.plot_hierarchically_linked_series(
bottom_series='Australia/ACT/Canberra/Other',
Y_df=plot_df,
models=['y', 'ETS/MinTrace_method-mint_shrink'],
level=[80, 90]
)
参考文献
- Hyndman, R.J. 和 Athanasopoulos, G. (2021). “预测:原则与实践,第3版: 第11章:预测层次和分组系列。” OTexts: 墨尔本,澳大利亚。OTexts.com/fpp3 访问于2022年7月。
- Shanika L. Wickramasuriya, George Athanasopoulos 和 Rob J. Hyndman. 通过迹最小化实现层次和分组时间序列的最佳预测协调。美国统计协会杂志, 114(526):804–819, 2019. doi: 10.1080/01621459.2018.1448825. URL https://robjhyndman.com/publications/mint/.
- Puwasala Gamakumara 博士论文。蒙纳士大学,计量经济学与商业统计 (2020). “概率预测协调”
If you find the code useful, please ⭐ us on Github