神经网络/机器学习预测

这个示例笔记本演示了HierarchicalForecast的调和方法与流行的机器学习库的兼容性，特别是NeuralForecast和MLForecast。

该笔记本利用NBEATS和XGBRegressor模型为TourismLarge层次数据集创建基础预测。之后，我们使用HierarchicalForecast来调和基础预测结果。

参考文献
- Boris N. Oreshkin, Dmitri Carpov, Nicolas Chapados, Yoshua Bengio（2019）。“N-BEATS：用于可解释时间序列预测的神经基础扩展分析”。网址：https://arxiv.org/abs/1905.10437
- Tianqi Chen和Carlos Guestrin。“XGBoost：一种可扩展的树提升系统”。发表于：第22届ACM SIGKDD国际知识发现与数据挖掘会议论文集。KDD ’16。美国加利福尼亚州旧金山：计算机协会，2016年，页码785–794。ISBN: 9781450342322。DOI: 10.1145/2939672.2939785。网址：https://doi.org/10.1145/2939672.2939785（引用于第26页）。

您可以使用CPU或GPU在Google Colab中运行这些实验。

1. 安装包

# %pip 安装 datasetsforecast hierarchicalforecast mlforecast neuralforecast 

import numpy as np
import pandas as pd

from datasetsforecast.hierarchical import HierarchicalData

from neuralforecast import NeuralForecast
from neuralforecast.models import NBEATS
from neuralforecast.losses.pytorch import GMM

from mlforecast import MLForecast
from mlforecast.utils import PredictionIntervals
import xgboost as xgb

#获取层次协调方法及评估
from hierarchicalforecast.methods import BottomUp, ERM, MinTrace
from hierarchicalforecast.utils import HierarchicalPlot
from hierarchicalforecast.core import HierarchicalReconciliation
from hierarchicalforecast.evaluation import scaled_crps

2. 加载层次数据集

这个详细的澳大利亚旅游数据集来自国家游客调查，由澳大利亚旅游研究机构管理，包含1998年至2016年间的555个月度时间序列，按地理位置和旅行目的组织。自然地理层级包括七个州，进一步分为27个区域和76个地区。旅行目的分类包括假期、探访朋友和亲戚（VFR）、商务及其他。MinT（Wickramasuriya等人，2019）等其他层次预测研究曾在过去使用该数据集。该数据集可以在MinT对账网页中访问，尽管还有其他来源可用。

地理区划	每个区划的系列数量	每个目的的系列数量	总计
澳大利亚	1	4	5
各州	7	28	35
区域	27	108	135
地区	76	304	380
总计	111	444	555

Y_df, S_df, tags = HierarchicalData.load('./data', 'TourismLarge')
Y_df['ds'] = pd.to_datetime(Y_df['ds'])

Y_df.head()

	unique_id	ds	y
0	TotalAll	1998-01-01	45151.071280
1	TotalAll	1998-02-01	17294.699551
2	TotalAll	1998-03-01	20725.114184
3	TotalAll	1998-04-01	25388.612353
4	TotalAll	1998-05-01	20330.035211

可视化聚合矩阵。

hplot = HierarchicalPlot(S=S_df, tags=tags)
hplot.plot_summing_matrix()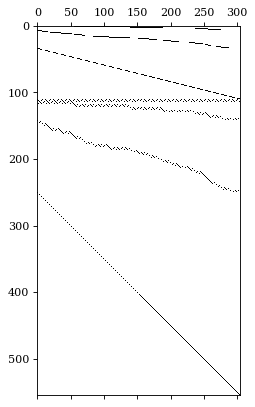

将数据框拆分为训练/测试集。

def sort_hier_df(Y_df, S_df):
    # 按字典顺序排序唯一标识符
    Y_df.unique_id = Y_df.unique_id.astype('category')
    Y_df.unique_id = Y_df.unique_id.cat.set_categories(S_df.index)
    Y_df = Y_df.sort_values(by=['unique_id', 'ds'])
    return Y_df

Y_df = sort_hier_df(Y_df, S_df)

horizon = 12
Y_test_df = Y_df.groupby('unique_id').tail(horizon)
Y_train_df = Y_df.drop(Y_test_df.index)

3. 拟合和预测模型

HierarchicalForecast与许多不同的机器学习模型兼容。这里，我们展示两个示例：
1. NBEATS，一种基于多层感知器的深度神经网络架构。
2. XGBRegressor，一种基于树的架构。

level = np.arange(0, 100, 2)
qs = [[50-lv/2, 50+lv/2] for lv in level]
quantiles = np.sort(np.concatenate(qs)/100)

#拟合/预测 从NeuralForecast使用NBEATS
nbeats = NBEATS(h=horizon,
              input_size=2*horizon,
              loss=GMM(n_components=10, quantiles=quantiles),
              scaler_type='robust',
              max_steps=2000)
nf = NeuralForecast(models=[nbeats], freq='MS')
nf.fit(df=Y_train_df)
Y_hat_nf = nf.predict()
insample_nf = nf.predict_insample(step_size=horizon)

#拟合/预测 来自MLForecast的XGBRegressor
mf = MLForecast(models=[xgb.XGBRegressor()], 
                freq='MS',
                lags=[1,2,12,24],
                date_features=['month'],
                )
mf.fit(Y_train_df, fitted=True, prediction_intervals=PredictionIntervals(n_windows=10, h=horizon)) 
Y_hat_mf = mf.predict(horizon, level=level).set_index('unique_id')
insample_mf = mf.forecast_fitted_values()

Y_hat_nf

	ds	NBEATS	NBEATS-lo-98.0	NBEATS-lo-96.0	NBEATS-lo-94.0	NBEATS-lo-92.0	NBEATS-lo-90.0	NBEATS-lo-88.0	NBEATS-lo-86.0	NBEATS-lo-84.0	...	NBEATS-hi-80.0	NBEATS-hi-82.0	NBEATS-hi-84.0	NBEATS-hi-86.0	NBEATS-hi-88.0	NBEATS-hi-90.0	NBEATS-hi-92.0	NBEATS-hi-94.0	NBEATS-hi-96.0	NBEATS-hi-98.0
unique_id
TotalAll	2016-01-01	44525.652344	21232.554688	26024.839844	27435.285156	28136.705078	28766.150391	29569.240234	30344.240234	31163.099609	...	51812.953125	52171.792969	52628.562500	52890.750000	53160.312500	54025.210938	54451.109375	55651.007812	57686.027344	61461.066406
TotalAll	2016-02-01	20819.431641	18020.289062	18314.943359	18480.269531	18612.464844	18695.382812	18807.242188	18912.910156	19027.187500	...	22719.998047	22802.921875	22887.734375	23031.005859	23133.865234	23230.322266	23406.496094	23622.166016	23887.796875	24165.496094
TotalAll	2016-03-01	23676.291016	19303.222656	19684.693359	19928.400391	20150.691406	20319.113281	20499.980469	20632.185547	20748.207031	...	26215.312500	26291.195312	26402.853516	26578.257812	26848.179688	27054.107422	27310.746094	27723.867188	28211.294922	29011.082031
TotalAll	2016-04-01	27978.587891	23936.988281	24329.892578	24532.740234	24735.703125	24902.812500	25165.074219	25256.669922	25489.455078	...	30192.365234	30278.451172	30339.017578	30381.443359	30465.722656	30574.056641	30682.609375	30860.427734	31032.648438	31199.992188
TotalAll	2016-05-01	22810.310547	20037.218750	20194.531250	20387.541016	20510.244141	20594.226562	20675.720703	20767.025391	20876.550781	...	24975.916016	25149.097656	25240.177734	25401.996094	25577.400391	25800.574219	26132.904297	26559.906250	27273.566406	28567.857422
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
GBDOth	2016-08-01	3.384338	-31.891897	-15.230768	-1.954657	-1.143704	-0.994592	-0.947800	-0.884839	-0.824748	...	9.635074	10.517044	11.374988	12.784556	14.568413	22.581669	37.880905	51.512486	62.645977	81.495415
GBDOth	2016-09-01	4.842800	-41.682514	-23.578377	-6.487054	-1.238661	-1.024779	-0.927368	-0.856639	-0.758568	...	11.743630	12.755230	14.384780	16.579344	19.425726	36.155537	44.394543	60.144749	78.533859	101.363129
GBDOth	2016-10-01	4.466261	-21.124041	-1.662255	-1.157058	-0.949211	-0.857361	-0.755605	-0.699540	-0.659419	...	10.405193	11.605769	12.686687	14.218900	19.963741	26.705273	34.361160	51.898552	68.361931	89.458908
GBDOth	2016-11-01	3.689114	-22.615982	-11.813770	-1.530864	-1.049960	-0.922807	-0.868391	-0.802971	-0.723462	...	8.213260	8.837670	10.219457	12.300932	13.135829	23.325760	37.628525	43.993382	63.594315	84.825226
GBDOth	2016-12-01	3.994789	-38.856083	-24.361221	-7.503808	-1.199999	-1.003695	-0.880594	-0.788414	-0.737489	...	9.881157	11.406334	12.636977	15.831536	26.059269	32.270000	37.316460	51.765774	68.933304	91.916100

6660 rows × 102 columns

Y_hat_mf

	ds	XGBRegressor	XGBRegressor-lo-98	XGBRegressor-lo-96	XGBRegressor-lo-94	XGBRegressor-lo-92	XGBRegressor-lo-90	XGBRegressor-lo-88	XGBRegressor-lo-86	XGBRegressor-lo-84	...	XGBRegressor-hi-80	XGBRegressor-hi-82	XGBRegressor-hi-84	XGBRegressor-hi-86	XGBRegressor-hi-88	XGBRegressor-hi-90	XGBRegressor-hi-92	XGBRegressor-hi-94	XGBRegressor-hi-96	XGBRegressor-hi-98
unique_id
TotalAll	2016-01-01	43060.226562	38276.974483	38677.670530	39078.366577	39479.062624	39879.758671	40009.218877	40041.809140	40074.399403	...	45980.873195	46013.463459	46046.053722	46078.643985	46111.234248	46240.694454	46641.390501	47042.086548	47442.782595	47843.478642
TotalAll	2016-02-01	18008.296875	14687.962868	14813.816467	14939.670066	15065.523666	15191.377265	15247.400539	15278.484410	15309.568281	...	20644.857726	20675.941597	20707.025469	20738.109340	20769.193211	20825.216485	20951.070084	21076.923684	21202.777283	21328.630882
TotalAll	2016-03-01	20694.080078	16407.351099	16594.149043	16780.946987	16967.744931	17154.542875	17209.434677	17217.217141	17224.999606	...	24147.595620	24155.378085	24163.160550	24170.943015	24178.725480	24233.617281	24420.415225	24607.213169	24794.011113	24980.809057
TotalAll	2016-04-01	24474.349609	20859.120558	20978.737726	21098.354893	21217.972060	21337.589227	21380.287167	21395.513953	21410.740739	...	27507.504906	27522.731693	27537.958479	27553.185266	27568.412052	27611.109991	27730.727159	27850.344326	27969.961493	28089.578660
TotalAll	2016-05-01	19281.087891	15045.235849	15460.108990	15874.982131	16289.855271	16704.728412	16861.927796	16927.100837	16992.273878	...	21439.555822	21504.728863	21569.901904	21635.074945	21700.247986	21857.447369	22272.320510	22687.193651	23102.066792	23516.939933
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
GBDOth	2016-08-01	11.040442	-0.720264	0.934877	2.590017	4.245157	5.900298	6.396993	6.479957	6.562921	...	15.352035	15.435000	15.517964	15.600928	15.683892	16.180587	17.835727	19.490868	21.146008	22.801149
GBDOth	2016-09-01	6.440751	-0.275863	-0.182214	-0.088566	0.005083	0.098732	0.123376	0.123376	0.123376	...	12.758126	12.758126	12.758126	12.758126	12.758126	12.782771	12.876419	12.970068	13.063716	13.157365
GBDOth	2016-10-01	9.995112	2.407870	2.407870	2.407870	2.407870	2.407870	2.407870	2.407870	2.407870	...	17.582355	17.582355	17.582355	17.582355	17.582355	17.582355	17.582355	17.582355	17.582355	17.582355
GBDOth	2016-11-01	6.747566	2.791389	2.791389	2.791389	2.791389	2.791389	2.791389	2.791389	2.791389	...	10.703742	10.703742	10.703742	10.703742	10.703742	10.703742	10.703742	10.703742	10.703742	10.703742
GBDOth	2016-12-01	7.367904	2.349200	2.349200	2.349200	2.349200	2.349200	2.349200	2.349200	2.349200	...	12.386609	12.386609	12.386609	12.386609	12.386609	12.386609	12.386609	12.386609	12.386609	12.386609

6660 rows × 102 columns

4. 预测的协调

通过最小的解析，我们可以使用不同的层次预测协调方法来协调原始输出预测。

reconcilers = [
    ERM(method='closed'),
    BottomUp(),
    MinTrace('ols'),
]
hrec = HierarchicalReconciliation(reconcilers=reconcilers)

Y_rec_nf = hrec.reconcile(Y_hat_df=Y_hat_nf, Y_df=insample_nf, S=S_df, tags=tags, level=level)
Y_rec_mf = hrec.reconcile(Y_hat_df=Y_hat_mf, Y_df=insample_mf, S=S_df, tags=tags, level=level)

5. 评估

为了进行评估，我们使用Rangapuram（2021）提出的CRPS的缩放变体，以测量预测分位数y_hat与观测值y之间的准确性。

\[ \mathrm{sCRPS}(\hat{F}_{\tau}, \mathbf{y}_{\tau}) = \frac{2}{N} \sum_{i} \int^{1}_{0} \frac{\mathrm{QL}(\hat{F}_{i,\tau}, y_{i,\tau})_{q}}{\sum_{i} | y_{i,\tau} |} dq \]

rec_model_names_nf = ['NBEATS/BottomUp', 'NBEATS/MinTrace_method-ols', 'NBEATS/ERM_method-closed_lambda_reg-0.01']
rec_model_names_mf = ['XGBRegressor/BottomUp', 'XGBRegressor/MinTrace_method-ols', 'XGBRegressor/ERM_method-closed_lambda_reg-0.01']

n_quantiles = len(quantiles)
n_series = len(S_df)

for name in rec_model_names_nf:
    quantile_columns = [col for col in Y_rec_nf.columns if (name+'-lo') in col or (name+'-hi') in col]
    y_rec  = Y_rec_nf[quantile_columns].values 
    y_test = Y_test_df['y'].values

    y_rec  = y_rec.reshape(n_series, horizon, n_quantiles)
    y_test = y_test.reshape(n_series, horizon)
    scrps  = scaled_crps(y=y_test, y_hat=y_rec, quantiles=quantiles)
    print("{:<50} {:.3f}".format(name+":", scrps))

for name in rec_model_names_mf:
    quantile_columns = [col for col in Y_rec_mf.columns if (name+'-lo') in col or (name+'-hi') in col]
    y_rec  = Y_rec_mf[quantile_columns].values 
    y_test = Y_test_df['y'].values

    y_rec  = y_rec.reshape(n_series, horizon, n_quantiles)
    y_test = y_test.reshape(n_series, horizon)
    scrps  = scaled_crps(y=y_test, y_hat=y_rec, quantiles=quantiles)
    print("{:<50} {:.3f}".format(name+":", scrps))

NBEATS/BottomUp:                                   0.129
NBEATS/MinTrace_method-ols:                        0.129
NBEATS/ERM_method-closed_lambda_reg-0.01:          0.179
XGBRegressor/BottomUp:                             0.134
XGBRegressor/MinTrace_method-ols:                  0.178
XGBRegressor/ERM_method-closed_lambda_reg-0.01:    0.177

6. 可视化

plot_nf = pd.concat([Y_df.set_index(['unique_id', 'ds']), 
                     Y_rec_nf.set_index('ds', append=True)], axis=1)
plot_nf = plot_nf.reset_index('ds')

plot_mf = pd.concat([Y_df.set_index(['unique_id', 'ds']), 
                     Y_rec_mf.set_index('ds', append=True)], axis=1)
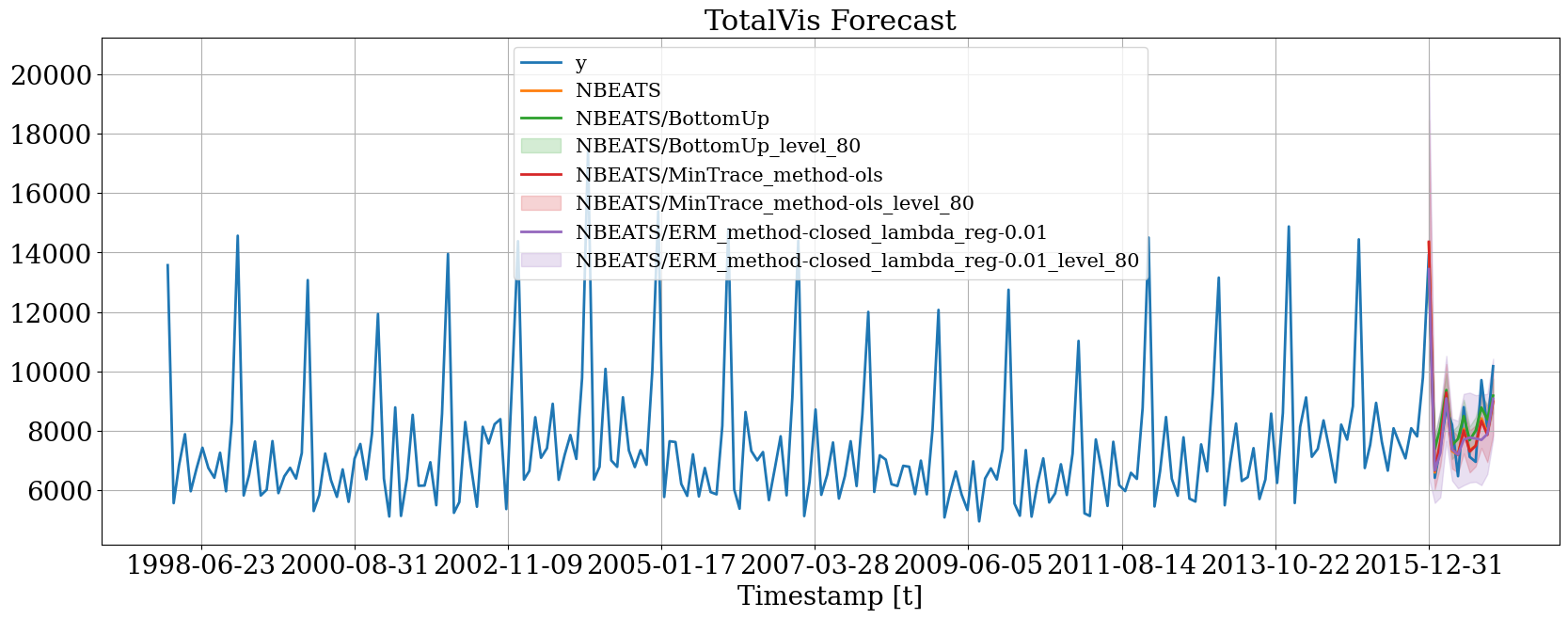
plot_mf = plot_mf.reset_index('ds')

hplot.plot_series(
    series='TotalVis',
    Y_df=plot_nf, 
    models=['y', 'NBEATS', 'NBEATS/BottomUp', 'NBEATS/MinTrace_method-ols', 'NBEATS/ERM_method-closed_lambda_reg-0.01'],
    level=[80]
)

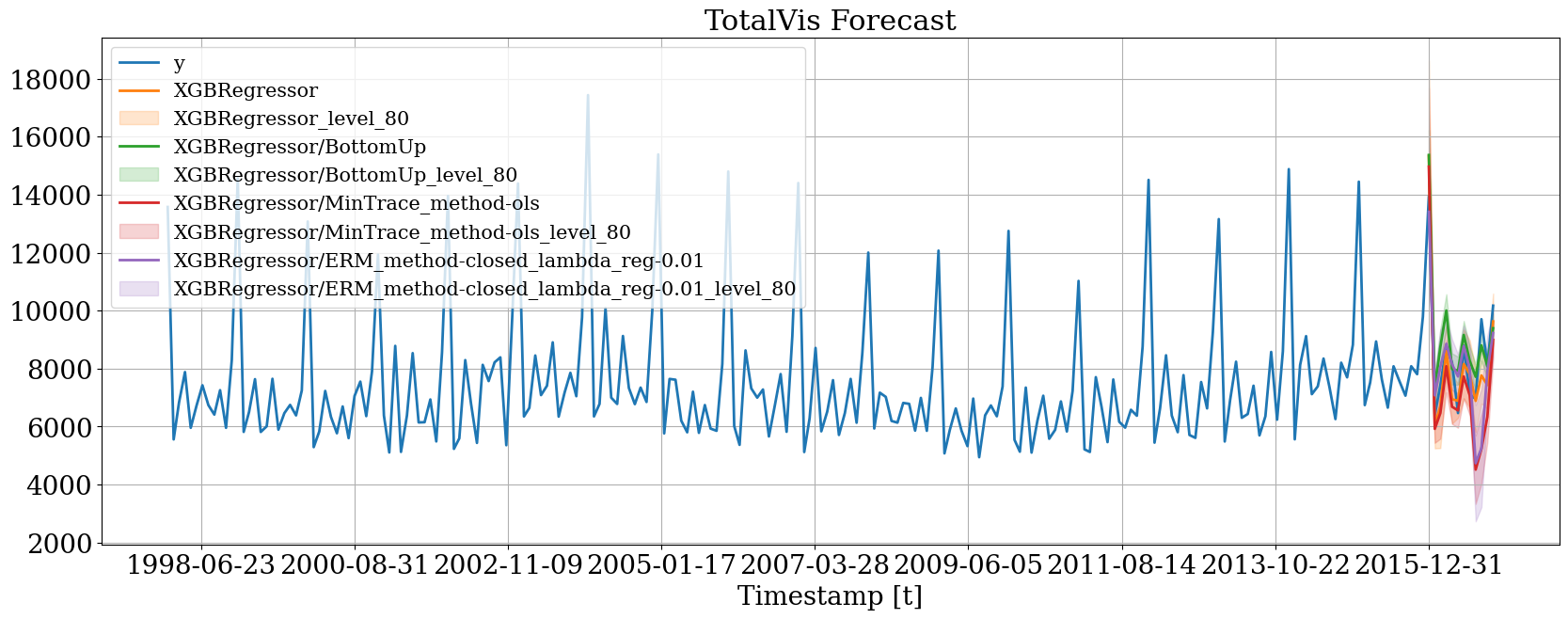
hplot.plot_series(
    series='TotalVis',
    Y_df=plot_mf, 
    models=['y', 'XGBRegressor', 'XGBRegressor/BottomUp', 'XGBRegressor/MinTrace_method-ols', 'XGBRegressor/ERM_method-closed_lambda_reg-0.01'],
    level=[80]
)

If you find the code useful, please ⭐ us on Github