介绍

使用 HierarchialForecast 进行层次预测的介绍

您可以使用CPU或GPU在Google Colab中运行这些实验。

在Colab中打开

1. 层次序列

在许多应用中，一组时间序列是分层组织的。例子包括地理层级、产品或类别的存在，这些层级定义了不同类型的聚合。

在这种情况下，预测者通常需要为所有的分解序列和聚合序列提供预测。一个自然的愿望是这些预测是“一致的”，即底层序列恰好加起来等于聚合序列的预测值。

图 1. 一个两级时间序列的层级结构，包含四个底层变量。

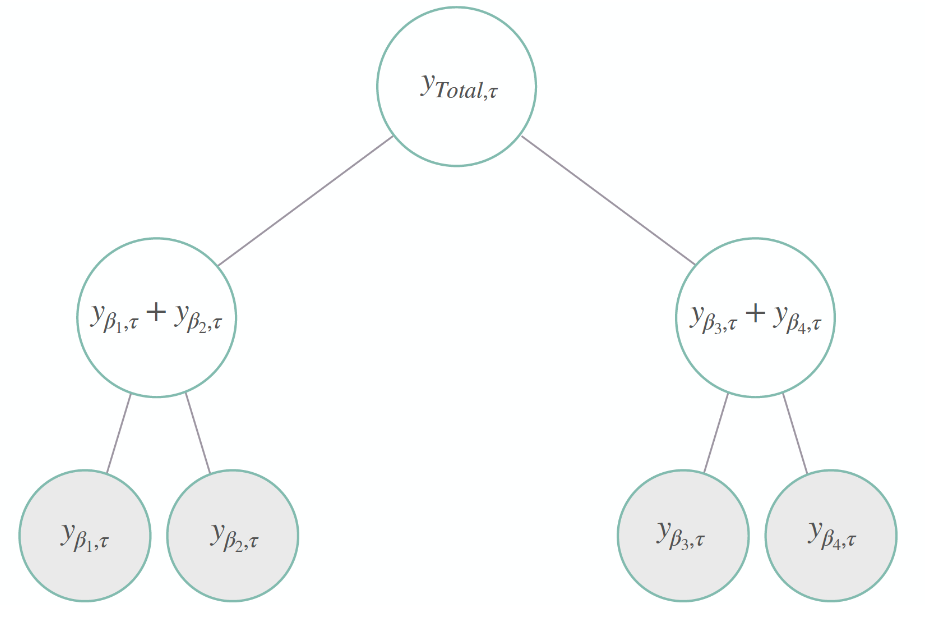
图1展示了一个简单的层次结构，其中我们有四个底层系列、两个中层系列，顶层表示总聚合。其层次聚合或一致性约束为：

\[\begin{align} y_{\mathrm{Total},\tau} = y_{\beta_{1},\tau}+y_{\beta_{2},\tau}+y_{\beta_{3},\tau}+y_{\beta_{4},\tau} \qquad \qquad \qquad \qquad \qquad \\ \mathbf{y}_{[a],\tau}=\left[y_{\mathrm{Total},\tau},\; y_{\beta_{1},\tau}+y_{\beta_{2},\tau},\;y_{\beta_{3},\tau}+y_{\beta_{4},\tau}\right]^{\intercal} \qquad \mathbf{y}_{[b],\tau}=\left[ y_{\beta_{1},\tau},\; y_{\beta_{2},\tau},\; y_{\beta_{3},\tau},\; y_{\beta_{4},\tau} \right]^{\intercal} \end{align}\]

幸运的是，这些约束可以用以下矩阵紧凑地表示：

\[\begin{align} \mathbf{S}_{[a,b][b]} = \begin{bmatrix} \mathbf{A}_{\mathrm{[a][b]}} \\ \\ \\ \mathbf{I}_{\mathrm{[b][b]}} \\ \\ \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \end{align}\]

其中 \(\mathbf{A}_{[a,b][b]}\) 将底部系列聚合到上层，\(\mathbf{I}_{\mathrm{[b][b]}}\) 是单位矩阵。层次系列的表示为：

\[\begin{align} \mathbf{y}_{[a,b],\tau} = \mathbf{S}_{[a,b][b]} \mathbf{y}_{[b],\tau} \end{align}\]

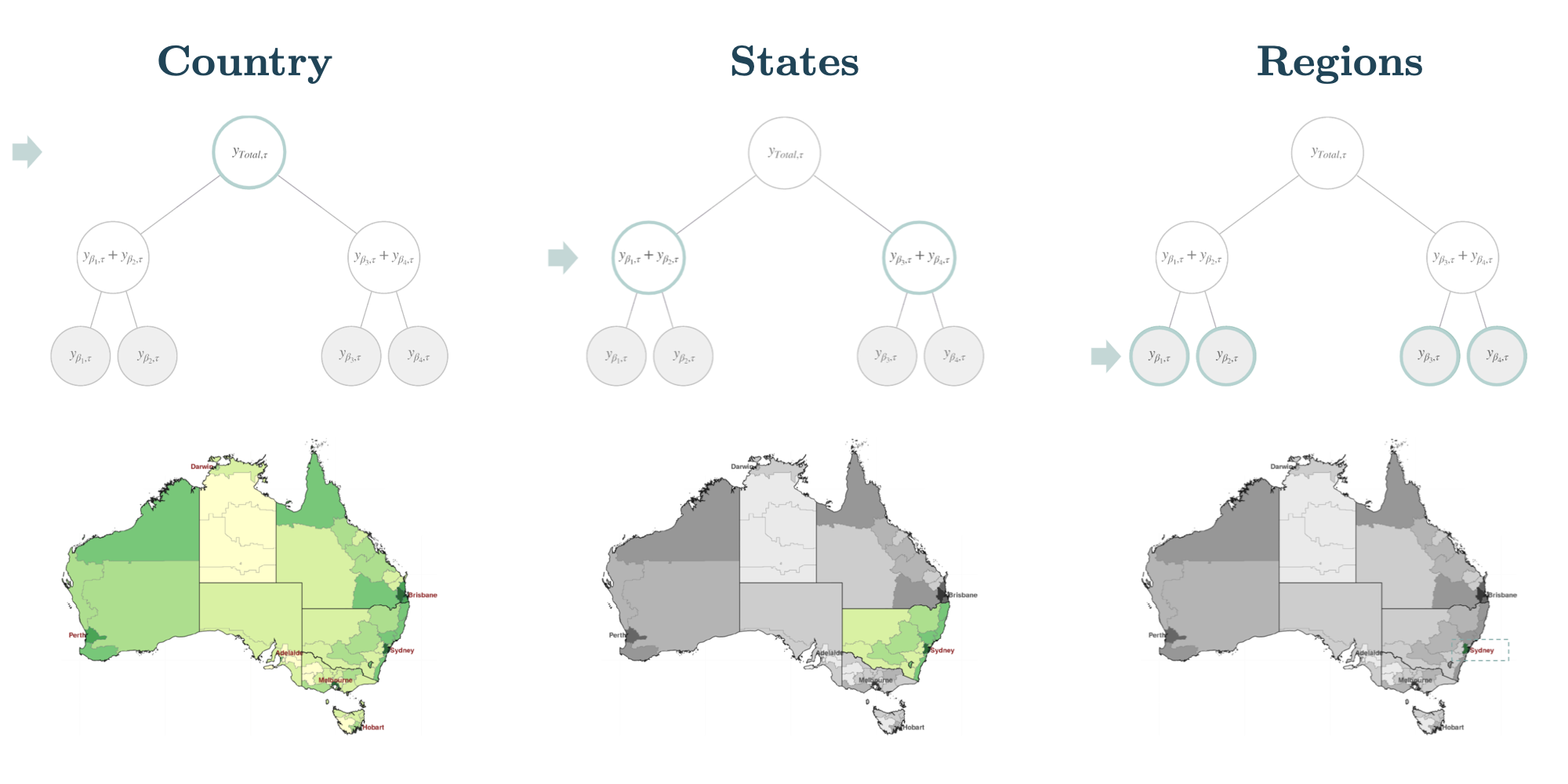
为了可视化一个例子，如图2所示。可以认为层次时间序列结构的层级代表不同的地理聚合。例如，在图2中，最顶层是一个国家内系列的总聚合，中间层是各个州，底层是各个地区。

图2. 一个层次结构可以由地理级别组成。在这个例子中，顶层对应于国家聚合，中层对应于州，底层对应于地区。

2. 层次预测

为了实现“一致性”，大多数统计解决方案针对层次预测挑战实施了两阶段的协调过程。
1. 首先，我们获得一组基础预测 \(\mathbf{\hat{y}}_{[a,b],\tau}\)
2. 然后，我们将其协调为一致的预测 \(\mathbf{\tilde{y}}_{[a,b],\tau}\)。

大多数层次协调方法可通过以下变换来表示：

\[\begin{align} \tilde{\mathbf{y}}_{[a,b],\tau} = \mathbf{S}_{[a,b][b]} \mathbf{P}_{[b][a,b]} \hat{\mathbf{y}}_{[a,b],\tau} \end{align}\]

HierarchicalForecast库提供了一组用于该任务的Python集合，包括调和方法、数据集、评估和可视化工具。在其可用的调和方法中，我们有BottomUp、TopDown、MiddleOut、MinTrace和ERM。在其概率一致性方法中，我们有Normality、Bootstrap和PERMBU。

3. 最小示例

%%capture
!pip install hierarchicalforecast
!pip install -U numba statsforecast datasetsforecast

整理数据

import numpy as np
import pandas as pd

我们将创建一个合成数据集，以说明类似于图1所示的层次时间序列结构。

我们将创建一个具有两个层级的结构，并包含四个底层系列，其中系列的聚合是显而易见的。

# 创建图1. 合成底部数据
ds = pd.date_range(start='2000-01-01', end='2000-08-01', freq='MS')
y_base = np.arange(1,9)
r1 = y_base * (10**1)
r2 = y_base * (10**1)
r3 = y_base * (10**2)
r4 = y_base * (10**2)

ys = np.concatenate([r1, r2, r3, r4])
ds = np.tile(ds, 4)
unique_ids = ['r1'] * 8 + ['r2'] * 8 + ['r3'] * 8 + ['r4'] * 8
top_level = 'Australia'
middle_level = ['State1'] * 16 + ['State2'] * 16
bottom_level = unique_ids

bottom_df = dict(ds=ds,
                 top_level=top_level, 
                 middle_level=middle_level, 
                 bottom_level=bottom_level,
                 y=ys)
bottom_df = pd.DataFrame(bottom_df)
bottom_df.groupby('bottom_level').head(2)
ds top_level middle_level bottom_level y
0 2000-01-01 Australia State1 r1 10
1 2000-02-01 Australia State1 r1 20
8 2000-01-01 Australia State1 r2 10
9 2000-02-01 Australia State1 r2 20
16 2000-01-01 Australia State2 r3 100
17 2000-02-01 Australia State2 r3 200
24 2000-01-01 Australia State2 r4 100
25 2000-02-01 Australia State2 r4 200

先前介绍的层次系列 \(\mathbf{y}_{[a,b]\tau}\) 被捕获在 Y_hier_df 数据框中。

聚合约束矩阵 \(\mathbf{S}_{[a][b]}\) 被捕获在 S_df 数据框中。

最后，tags 包含一个列表，在 Y_hier_df 中组成每个层次级别，例如 tags['top_level'] 包含 Australia 的聚合系列索引。

from hierarchicalforecast.utils import aggregate
# 创建层级结构和约束
hierarchy_levels = [['top_level'],
                    ['top_level', 'middle_level'],
                    ['top_level', 'middle_level', 'bottom_level']]
Y_hier_df, S_df, tags = aggregate(df=bottom_df, spec=hierarchy_levels)
Y_hier_df = Y_hier_df.reset_index()
print('S_df.shape', S_df.shape)
print('Y_hier_df.shape', Y_hier_df.shape)
print("tags['top_level']", tags['top_level'])
S_df.shape (7, 4)
Y_hier_df.shape (56, 3)
tags['top_level'] ['Australia']
/Users/cchallu/opt/anaconda3/envs/hierarchicalforecast/lib/python3.10/site-packages/sklearn/preprocessing/_encoders.py:828: FutureWarning: `sparse` was renamed to `sparse_output` in version 1.2 and will be removed in 1.4. `sparse_output` is ignored unless you leave `sparse` to its default value.
  warnings.warn(
Y_hier_df.groupby('unique_id').head(2)
unique_id ds y
0 Australia 2000-01-01 220.0
1 Australia 2000-02-01 440.0
8 Australia/State1 2000-01-01 20.0
9 Australia/State1 2000-02-01 40.0
16 Australia/State2 2000-01-01 200.0
17 Australia/State2 2000-02-01 400.0
24 Australia/State1/r1 2000-01-01 10.0
25 Australia/State1/r1 2000-02-01 20.0
32 Australia/State1/r2 2000-01-01 10.0
33 Australia/State1/r2 2000-02-01 20.0
40 Australia/State2/r3 2000-01-01 100.0
41 Australia/State2/r3 2000-02-01 200.0
48 Australia/State2/r4 2000-01-01 100.0
49 Australia/State2/r4 2000-02-01 200.0 
S_df
Australia/State1/r1 Australia/State1/r2 Australia/State2/r3 Australia/State2/r4
Australia 1.0 1.0 1.0 1.0
Australia/State1 1.0 1.0 0.0 0.0
Australia/State2 0.0 0.0 1.0 1.0
Australia/State1/r1 1.0 0.0 0.0 0.0
Australia/State1/r2 0.0 1.0 0.0 0.0
Australia/State2/r3 0.0 0.0 1.0 0.0
Australia/State2/r4 0.0 0.0 0.0 1.0

基础预测

接下来，我们使用naive模型为每个时间序列计算基础预测。请注意，Y_hat_df包含预测值，但它们并不一致。

%%capture
from statsforecast.models import Naive
from statsforecast.core import StatsForecast
# 划分训练集/测试集
Y_test_df  = Y_hier_df.groupby('unique_id').tail(4)
Y_train_df = Y_hier_df.drop(Y_test_df.index)

# 计算基准朴素预测
# 仔细识别正确的数据频率，此数据为季度数据。 'Q'
fcst = StatsForecast(df=Y_train_df,
                     models=[Naive()],
                     freq='Q', n_jobs=-1)
Y_hat_df = fcst.forecast(h=4, fitted=True)
Y_fitted_df = fcst.forecast_fitted_values()

对账

from hierarchicalforecast.methods import BottomUp
from hierarchicalforecast.core import HierarchicalReconciliation
# 您可以从我们的收藏中选择一个调解者。
reconcilers = [BottomUp()] # MinTrace(method='mint_shrink')
hrec = HierarchicalReconciliation(reconcilers=reconcilers)

Y_rec_df = hrec.reconcile(Y_hat_df=Y_hat_df, 
                          Y_df=Y_fitted_df,
                          S=S_df, tags=tags)
Y_rec_df.groupby('unique_id').head(2)
ds Naive Naive/BottomUp
unique_id
Australia 2000-06-30 880.0 880.0
Australia 2000-09-30 880.0 880.0
Australia/State1 2000-06-30 80.0 80.0
Australia/State1 2000-09-30 80.0 80.0
Australia/State2 2000-06-30 800.0 800.0
Australia/State2 2000-09-30 800.0 800.0
Australia/State1/r1 2000-06-30 40.0 40.0
Australia/State1/r1 2000-09-30 40.0 40.0
Australia/State1/r2 2000-06-30 40.0 40.0
Australia/State1/r2 2000-09-30 40.0 40.0
Australia/State2/r3 2000-06-30 400.0 400.0
Australia/State2/r3 2000-09-30 400.0 400.0
Australia/State2/r4 2000-06-30 400.0 400.0
Australia/State2/r4 2000-09-30 400.0 400.0

参考文献

If you find the code useful, please ⭐ us on Github