skimage.graph#
此模块提供基于图的图像处理工具。
这包括创建图像中像素的邻接图,找到图像中的中心像素,找到(最小成本)像素路径,合并和切割图等。
找到具有最高接近中心性的像素。 |
|
在区域邻接图上执行归一化图割。 |
|
合并权重小于阈值的区域。 |
|
执行 RAG 的层次合并。 |
|
创建图像中像素的邻接图。 |
|
基于区域边界的计算机RAG |
|
使用平均颜色计算区域邻接图。 |
|
如何使用 MCP 和 MCP_Geometric 类的简单示例。 |
|
找到通过一个 n 维数组从一边到另一边的最短路径。 |
|
在图像上显示一个区域邻接图。 |
|
一个用于在给定的 n 维成本数组中寻找最小成本路径的类。 |
|
使用距离加权最小成本函数连接源点。 |
|
通过 N 维成本数组找到最小成本路径。 |
|
在 n 维成本数组中找到距离加权的最小成本路径。 |
|
The Region Adjacency Graph (RAG) of an image, subclasses |
- skimage.graph.central_pixel(graph, nodes=None, shape=None, partition_size=100)[源代码][源代码]#
找到具有最高接近中心性的像素。
接近中心性是节点到其他所有节点最短距离总和的倒数。
- 参数:
- 图scipy.sparse.csr_matrix
图的稀疏矩阵表示。
- 节点int 数组
图像中每个节点在图中的展开索引。如果未提供,返回值将是输入图中的索引。
- 形状int 的元组
节点嵌入的图像形状。如果提供,返回的坐标是与输入形状相同维度的NumPy多索引。否则,返回的坐标是`nodes`中提供的展平索引。
- 分区大小整数
此函数计算图中每对节点之间的最短路径距离。这可能导致一个非常大的(N*N)矩阵。为了简单地提高性能,距离值是按 partition_size 大量计算的,从而仅需要 partition_size*N 的内存需求。
- 返回:
- 位置int 或 int 的元组
如果给出了形状,则为图像中中心像素的坐标。否则,为该像素的展平索引。
- 距离浮点数数组
从每个节点到每个其他可达节点的总距离之和。
- skimage.graph.cut_normalized(labels, rag, thresh=0.001, num_cuts=10, in_place=True, max_edge=1.0, *, rng=None)[源代码][源代码]#
在区域邻接图上执行归一化图割。
给定图像的标签及其相似性RAG,递归地对其执行双向归一化切割。所有属于无法进一步切割的子图的节点在输出中被分配一个唯一的标签。
- 参数:
- 标签ndarray
标签数组。
- ragRAG
区域邻接图。
- thresh浮动
阈值。如果 N-cut 的值超过 thresh,则子图将不再进一步细分。
- num_cuts整数
在确定最佳分割之前要执行的分割次数或 N 次分割。
- in_place布尔
如果设置,原地修改 rag。对于每个节点 n,该函数将设置一个新的属性
rag.nodes[n]['ncut label']。- max_edgefloat, 可选
RAG中一条边的最大可能值。这对应于同一区域之间的边。这用于在RAG中放置自环边。
- rng : {
numpy.random.Generator, int}, 可选toctree是一个 reStructuredText 指令 ,这是一个非常多功能的标记。指令可以有参数、选项和内容。 伪随机数生成器。默认情况下,使用 PCG64 生成器(参见
numpy.random.default_rng())。如果 rng 是整数,则用于为生成器设定种子。rng 用于确定
scipy.sparse.linalg.eigsh的起始点。
- 返回:
- 出ndarray
新的带标签数组。
参考文献
[1]Shi, J.; Malik, J., “归一化切割与图像分割”, 模式分析与机器智能, IEEE 交易, 卷. 22, 编号. 8, 页. 888-905, 2000年8月。
示例
>>> from skimage import data, segmentation, graph >>> img = data.astronaut() >>> labels = segmentation.slic(img) >>> rag = graph.rag_mean_color(img, labels, mode='similarity') >>> new_labels = graph.cut_normalized(labels, rag)
- skimage.graph.cut_threshold(labels, rag, thresh, in_place=True)[源代码][源代码]#
合并权重小于阈值的区域。
给定一个图像的标签及其RAG,通过合并节点间权重小于给定阈值的区域来输出新的标签。
- 参数:
- 标签ndarray
标签数组。
- ragRAG
区域邻接图。
- thresh浮动
阈值。通过权重较小的边连接的区域将被合并。
- in_place布尔
如果设置,原地修改 rag。该函数将移除权重小于 thresh 的边。如果设置为 False,该函数在继续之前会复制 rag。
- 返回:
- 出ndarray
新的标记数组。
参考文献
[1]Alain Tremeau 和 Philippe Colantoni 的 “应用于彩色图像分割的区域邻接图” DOI:10.1109/83.841950
示例
>>> from skimage import data, segmentation, graph >>> img = data.astronaut() >>> labels = segmentation.slic(img) >>> rag = graph.rag_mean_color(img, labels) >>> new_labels = graph.cut_threshold(labels, rag, 10)
- skimage.graph.merge_hierarchical(labels, rag, thresh, rag_copy, in_place_merge, merge_func, weight_func)[源代码][源代码]#
执行 RAG 的层次合并。
贪婪地合并最相似的一对节点,直到没有低于 thresh 的边剩余。
- 参数:
- 标签ndarray
标签数组。
- ragRAG
区域邻接图。
- thresh浮动
通过权重小于 thresh 的边连接的区域将被合并。
- rag_copy布尔
如果设置,则在修改前复制RAG。
- in_place_merge布尔
如果设置,节点将在原地合并。否则,将为每次合并创建一个新节点。
- merge_func可调用
此函数在合并两个节点之前被调用。对于合并 src 和 dst 的 RAG graph,它按如下方式调用
merge_func(graph, src, dst)。- weight_func可调用
计算合并节点相邻节点的新的权重的函数。这直接作为参数 weight_func 传递给 merge_nodes。
- 返回:
- 出ndarray
新的带标签数组。
- skimage.graph.pixel_graph(image, *, mask=None, edge_function=None, connectivity=1, spacing=None)[源代码][源代码]#
创建图像中像素的邻接图。
掩码为 True 的像素是返回图中节点,它们根据连通性参数与其邻居通过边连接。默认情况下,当给定掩码或图像本身就是掩码时,边的 值 是像素之间的欧几里得距离。
然而,如果给定的是一个没有掩码的整型或浮点型图像,边缘的值是相邻像素间强度差的绝对值,乘以欧几里得距离的权重。
- 参数:
- 图像数组
输入图像。如果图像是布尔类型的,它也将被用作掩码。
- 掩码布尔数组
使用哪些像素。如果为 None,则使用整个图像的图表。
- 边缘函数可调用
一个函数接受一个像素值数组、一个相邻像素值数组和一个距离数组,并返回一个边缘值。如果没有给出函数,边缘值就是距离。
- 连接性整数
像素邻域的方形连通性:允许的正交步数,以将一个像素视为邻居。详情请参见
scipy.ndimage.generate_binary_structure。- 间距浮点数元组
沿每个轴的像素间距。
- 返回:
- 图scipy.sparse.csr_matrix
一个稀疏邻接矩阵,其中条目 (i, j) 为 1 如果节点 i 和 j 是邻居,否则为 0。
- 节点int 数组
图的节点。这些对应于掩码中非零像素的raveled索引。
- skimage.graph.rag_boundary(labels, edge_map, connectivity=2)[源代码][源代码]#
基于区域边界的计算机RAG
给定图像的初始分割及其边缘图,该方法构建相应的区域邻接图(RAG)。RAG中的每个节点代表图像中具有相同标签的一组像素。两个相邻区域之间的权重是沿其边界在 edge_map 中的平均值。
- 标签ndarray
带标签的图像。
- edge_mapndarray
这应该与 labels 的形状相同。对于两个相邻区域之间的边界上的所有像素,edge_map 中相应像素的平均值是它们之间的边缘权重。
- 连接性int, 可选
彼此之间的平方距离小于 connectivity 的像素被视为相邻。其取值范围为 1 到 labels.ndim。其行为与
scipy.ndimage.generate_binary_structure中的 connectivity 参数相同。
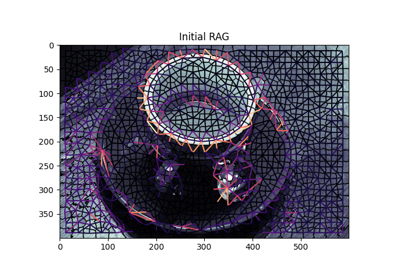
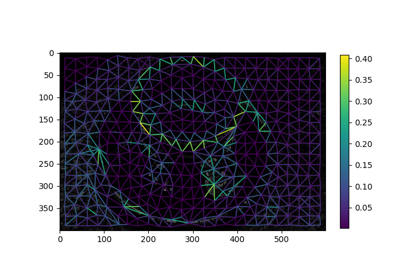
示例
>>> from skimage import data, segmentation, filters, color, graph >>> img = data.chelsea() >>> labels = segmentation.slic(img) >>> edge_map = filters.sobel(color.rgb2gray(img)) >>> rag = graph.rag_boundary(labels, edge_map)
- skimage.graph.rag_mean_color(image, labels, connectivity=2, mode='distance', sigma=255.0)[源代码][源代码]#
使用平均颜色计算区域邻接图。
给定一张图像及其初始分割,该方法构建相应的区域邻接图(RAG)。RAG中的每个节点代表 image 中具有相同标签 labels 的一组像素。两个相邻区域之间的权重表示根据 mode 参数,两个区域之间的相似性或差异性。
- 参数:
- 图像ndarray, 形状(M, N[, …, P], 3)
输入图像。
- 标签ndarray, 形状(M, N[, …, P])
标记图像。这应该比 image 少一个维度。如果 image 的维度是 (M, N, 3),那么 labels 的维度应该是 (M, N)。
- 连接性int, 可选
彼此之间的平方距离小于 connectivity 的像素被视为相邻。其取值范围为 1 到 labels.ndim。其行为与
scipy.ndimage.generate_binary_structure中的 connectivity 参数相同。- 模式{‘距离’, ‘相似性’}, 可选
分配边权重的策略。
‘distance’ : 两个相邻区域之间的权重是 \(|c_1 - c_2|\),其中 \(c_1\) 和 \(c_2\) 是两个区域的平均颜色。它表示它们平均颜色之间的欧几里得距离。
‘similarity’ : 两个相邻区域的权重是 \(e^{-d^2/sigma}\) ,其中 \(d=|c_1 - c_2|\),\(c_1\) 和 \(c_2\) 是两个区域的平均颜色。它表示两个区域的相似程度。
- sigmafloat, 可选
当 mode 为 “similarity” 时用于计算。它决定了两种颜色之间的接近程度,以便它们的对应边权重具有显著性。sigma 的值非常大时,任何两种颜色都会表现得像是相似的。
- 返回:
- 出RAG
区域邻接图。
参考文献
[1]Alain Tremeau 和 Philippe Colantoni 的 “应用于彩色图像分割的区域邻接图” DOI:10.1109/83.841950
示例
>>> from skimage import data, segmentation, graph >>> img = data.astronaut() >>> labels = segmentation.slic(img) >>> rag = graph.rag_mean_color(img, labels)
- skimage.graph.route_through_array(array, start, end, fully_connected=True, geometric=True)[源代码][源代码]#
如何使用 MCP 和 MCP_Geometric 类的简单示例。
关于路径查找算法的解释,请参阅 MCP 和 MCP_Geometric 类的文档。
- 参数:
- 返回:
- 路径列表
定义从 start 到 end 路径的 n-d 索引元组列表。
- 成本浮动
路径的成本。如果 geometric 为 False,路径的成本是
array沿路径的值的总和。如果 geometric 为 True,则进行更精细的计算(参见 MCP_Geometric 类的文档)。
参见
示例
>>> import numpy as np >>> from skimage.graph import route_through_array >>> >>> image = np.array([[1, 3], [10, 12]]) >>> image array([[ 1, 3], [10, 12]]) >>> # Forbid diagonal steps >>> route_through_array(image, [0, 0], [1, 1], fully_connected=False) ([(0, 0), (0, 1), (1, 1)], 9.5) >>> # Now allow diagonal steps: the path goes directly from start to end >>> route_through_array(image, [0, 0], [1, 1]) ([(0, 0), (1, 1)], 9.19238815542512) >>> # Cost is the sum of array values along the path (16 = 1 + 3 + 12) >>> route_through_array(image, [0, 0], [1, 1], fully_connected=False, ... geometric=False) ([(0, 0), (0, 1), (1, 1)], 16.0) >>> # Larger array where we display the path that is selected >>> image = np.arange((36)).reshape((6, 6)) >>> image array([[ 0, 1, 2, 3, 4, 5], [ 6, 7, 8, 9, 10, 11], [12, 13, 14, 15, 16, 17], [18, 19, 20, 21, 22, 23], [24, 25, 26, 27, 28, 29], [30, 31, 32, 33, 34, 35]]) >>> # Find the path with lowest cost >>> indices, weight = route_through_array(image, (0, 0), (5, 5)) >>> indices = np.stack(indices, axis=-1) >>> path = np.zeros_like(image) >>> path[indices[0], indices[1]] = 1 >>> path array([[1, 1, 1, 1, 1, 0], [0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 1]])
- skimage.graph.shortest_path(arr, reach=1, axis=-1, output_indexlist=False)[源代码][源代码]#
找到通过一个 n 维数组从一边到另一边的最短路径。
- 参数:
- arrfloat64 的 ndarray
- 达到int, 可选
默认情况下 (
reach = 1),最短路径每向前移动一步,只能向上或向下移动一行(即路径梯度限制为1)。reach 定义了在每一步中可以沿每个非轴维度跳过的元素数量。- 轴int, 可选
路径必须始终向前移动的轴(默认 -1)
- output_indexlistbool, 可选
参见返回值 p 以获取解释。
- 返回:
- pint 的可迭代对象
对于沿 axis 的每一步,最短路径的坐标。如果 output_indexlist 为 True,则路径作为 n-d 元组的列表返回,该列表索引到 arr 中。如果为 False,则路径作为数组返回,该数组列出了沿非轴维度的路径坐标,对于沿轴维度的每一步。也就是说,p.shape == (arr.shape[axis], arr.ndim-1),除了在返回之前对 p 进行压缩,因此如果 arr.ndim == 2,则 p.shape == (arr.shape[axis],)。
- 成本浮动
路径成本。这是路径上所有差异的绝对和。
- skimage.graph.show_rag(labels, rag, image, border_color='black', edge_width=1.5, edge_cmap='magma', img_cmap='bone', in_place=True, ax=None)[源代码][源代码]#
在图像上显示一个区域邻接图。
给定一个带有标签的图像及其对应的RAG,在图像上以指定颜色显示RAG的节点和边。边显示在图像中两个相邻区域的质心之间。
- 参数:
- 标签ndarray, 形状 (M, N)
带标签的图像。
- ragRAG
区域邻接图。
- 图像ndarray, 形状 (M, N[, 3])
输入图像。如果 colormap 是 None,图像应为 RGB 格式。
- border_color颜色规格,可选
绘制区域之间边界的颜色。
- edge_widthfloat, 可选
绘制 RAG 边缘的厚度。
- edge_cmap :
matplotlib.colors.Colormap, 可选matplotlib.colors.Colormap, 可选 用于绘制边缘的任何 matplotlib 颜色映射。
- img_cmap :
matplotlib.colors.Colormap, 可选matplotlib.colors.Colormap, 可选 任何用于绘制图像的 matplotlib 色图。如果设置为 None,则图像将按原样绘制。
- in_placebool, 可选
如果设置,RAG 会在原地修改。对于每个节点 n,该函数将设置一个新的属性
rag.nodes[n]['centroid']。- ax :
matplotlib.axes.Axes, 可选matplotlib.axes.Axes, 可选 要绘制的轴。如果未指定,则创建新的轴并绘制。
- 返回:
- lc
matplotlib.collections.LineCollection 表示图的边缘的一系列线条。它可以传递给
matplotlib.figure.Figure.colorbar()函数。
- lc
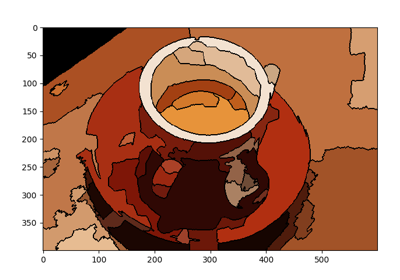
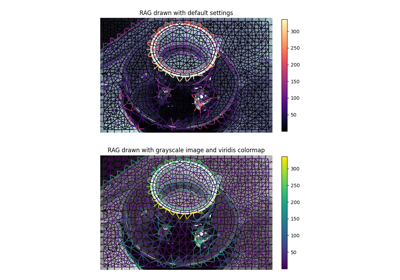
示例
>>> from skimage import data, segmentation, graph >>> import matplotlib.pyplot as plt >>> >>> img = data.coffee() >>> labels = segmentation.slic(img) >>> g = graph.rag_mean_color(img, labels) >>> lc = graph.show_rag(labels, g, img) >>> cbar = plt.colorbar(lc)
- class skimage.graph.MCP(costs, offsets=None, fully_connected=True, sampling=None)#
基类:
object一个用于在给定的 n 维成本数组中寻找最小成本路径的类。
给定一个 n 维成本数组,此类可用于通过该数组从任意一组点到另一组点找到最小成本路径。基本用法是初始化该类,并使用一个或多个起始索引(以及可选的结束索引列表)调用 find_costs()。之后,可以多次调用 traceback() 以从任何给定的结束位置找到到最近起始索引的路径。可以通过重复调用 find_costs() 来找到通过相同成本数组的新路径。
路径的成本简单地计算为路径上每个点的 costs 数组值的总和。另一方面,类 MCP_Geometric 考虑了对角线与轴向移动长度不同的事实,并相应地加权路径成本。
具有无限或负成本的数组元素将被简单地忽略,累计成本溢出为无限的路线也将被忽略。
- 参数:
- 成本ndarray
- 偏移量可迭代对象, 可选
偏移元组列表:每个偏移指定从给定的n维位置的有效移动。如果没有提供,将使用make_offsets()构造对应于单连接或全连接n维邻域的偏移,使用`fully_connected`参数值。
- 全连接bool, 可选
如果没有提供 offsets ,这将决定生成的邻域的连通性。如果为真,路径可以在 costs 数组的元素之间沿对角线移动;否则只允许轴向移动。
- 采样tuple, 可选
对于每个维度,指定两个单元格/体素之间的距离。如果没有给出或为None,则假定距离为单位距离。
- 属性:
- 偏移量ndarray
相当于提供给构造函数的 offsets,如果没有提供,则为请求的 n-d 邻域创建的偏移量。这些对于解释 find_costs() 方法返回的
traceback数组非常有用。
- __init__(costs, offsets=None, fully_connected=True, sampling=None)#
查看类文档。
- find_costs(starts, ends=None, find_all_ends=True, max_coverage=1.0, max_cumulative_cost=None, max_cost=None)#
从给定的起点找到最小成本路径。
此方法从指定的起始索引之一找到到达指定结束索引的最小成本路径。如果没有给出结束位置,则将找到到达成本数组中每个位置的最小成本路径。
- 参数:
- 开始可迭代对象
一个 n-d 起始索引列表(其中 n 是 costs 数组的维度)。将找到到最近/最便宜起始点的最小成本路径。
- 结束可迭代对象, 可选
一个以 n-d 结尾的索引列表。
- find_all_endsbool, 可选
如果为 ‘True’(默认),将找到到每个指定结束位置的最小成本路径;否则,算法将在找到到任何结束位置的路径时停止。(如果没有指定 ends,则此参数无效。)
- 返回:
- 累计成本ndarray
与 costs 数组形状相同;此数组记录从最近的/最便宜的起始索引到每个考虑的索引的最小成本路径。(如果指定了 ends,则不一定考虑数组中的所有元素:未评估的位置将具有累积成本 inf。如果 find_all_ends 为 ‘False’,则只有指定的结束位置之一将具有有限的累积成本。)
- 回溯ndarray
与 costs 数组形状相同;此数组包含从其前一个索引到任何给定索引的偏移量。偏移索引索引到 offsets 属性,该属性是一个 n-d 偏移量的数组。在 2-d 情况下,如果 offsets[traceback[x, y]] 是 (-1, -1),这意味着在到某个起始位置的最小成本路径中,[x, y] 的前一个索引是 [x+1, y+1]。请注意,如果 offset_index 是 -1,则给定索引未被考虑。
- goal_reached(index, cumcost)#
int goal_reached(int index, float cumcost) 每次从堆中弹出一个索引后,在检查邻居之前,都会调用此方法。
此方法可以被重载以修改MCP算法的行为。例如,可能会在达到某个累积成本时停止算法,或者在前沿距离种子点一定距离时停止算法。
如果算法不应检查当前点的邻居,此方法应返回 1;如果算法已完成,则应返回 2。
- offsets#
!! 由 numpydoc 处理 !!
- traceback(end)#
通过预先计算的回溯数组追踪最小成本路径。
这个便利函数从提供给 find_costs() 的起始索引之一重建到给定结束位置的最小成本路径,该函数必须在之前调用过 find_costs()。在 find_costs() 运行后,可以多次调用此函数。
- 参数:
- 结束可迭代对象
costs 数组的 n 维索引。
- 返回:
- 回溯n-d 元组列表
一个指向 costs 数组的索引列表,从传递给 find_costs() 的起始位置之一开始,并以给定的 end 索引结束。这些索引指定了从任意给定的起始索引到 end 索引的最小成本路径。(该路径的总成本可以从 find_costs() 返回的 cumulative_costs 数组中读取。)
- class skimage.graph.MCP_Connect(costs, offsets=None, fully_connected=True)#
基类:
MCP使用距离加权最小成本函数连接源点。
每个种子点同时生长出一个前端,同时跟踪前端的起源。当两个前端相遇时,调用 create_connection()。此方法必须被重载,以便以适合应用程序的方式处理找到的边缘。
- __init__(*args, **kwargs)#
- create_connection(id1, id2, tb1, tb2, cost1, cost2)#
create_connection id1, id2, pos1, pos2, cost1, cost2)
重载此方法以跟踪在MCP处理过程中发现的连接。请注意,具有相同ID的连接可能会被多次发现(但具有不同的位置和成本)。
当调用此方法时,这两个点都已被“冻结”,MCP算法将不会再访问它们。
- 参数:
- id1整数
第一个邻居起源的种子点ID。
- id2整数
第二个邻居起源的种子点ID。
- pos1元组
连接中第一个邻居的索引。
- pos2元组
连接中第二个邻居的索引。
- 成本1浮动
在 pos1 处的累计成本。
- 成本2浮动
在 pos2 处的累计成本。
- find_costs(starts, ends=None, find_all_ends=True, max_coverage=1.0, max_cumulative_cost=None, max_cost=None)#
从给定的起点找到最小成本路径。
此方法从指定的起始索引之一找到到达指定结束索引的最小成本路径。如果没有给出结束位置,则将找到到达成本数组中每个位置的最小成本路径。
- 参数:
- 开始可迭代对象
一个 n-d 起始索引列表(其中 n 是 costs 数组的维度)。将找到到最近/最便宜起始点的最小成本路径。
- 结束可迭代对象, 可选
一个以 n-d 结尾的索引列表。
- find_all_endsbool, 可选
如果为 ‘True’(默认),将找到到每个指定结束位置的最小成本路径;否则,算法将在找到到任何结束位置的路径时停止。(如果没有指定 ends,则此参数无效。)
- 返回:
- 累计成本ndarray
与 costs 数组形状相同;此数组记录从最近的/最便宜的起始索引到每个考虑的索引的最小成本路径。(如果指定了 ends,则不一定考虑数组中的所有元素:未评估的位置将具有累积成本 inf。如果 find_all_ends 为 ‘False’,则只有指定的结束位置之一将具有有限的累积成本。)
- 回溯ndarray
与 costs 数组形状相同;此数组包含从其前一个索引到任何给定索引的偏移量。偏移索引索引到 offsets 属性,该属性是一个 n-d 偏移量的数组。在 2-d 情况下,如果 offsets[traceback[x, y]] 是 (-1, -1),这意味着在到某个起始位置的最小成本路径中,[x, y] 的前一个索引是 [x+1, y+1]。请注意,如果 offset_index 是 -1,则给定索引未被考虑。
- goal_reached(index, cumcost)#
int goal_reached(int index, float cumcost) 每次从堆中弹出一个索引后,在检查邻居之前,都会调用此方法。
此方法可以被重载以修改MCP算法的行为。例如,可能会在达到某个累积成本时停止算法,或者在前沿距离种子点一定距离时停止算法。
如果算法不应检查当前点的邻居,此方法应返回 1;如果算法已完成,则应返回 2。
- offsets#
!! 由 numpydoc 处理 !!
- traceback(end)#
通过预先计算的回溯数组追踪最小成本路径。
这个便利函数从提供给 find_costs() 的起始索引之一重建到给定结束位置的最小成本路径,该函数必须在之前调用过 find_costs()。在 find_costs() 运行后,可以多次调用此函数。
- 参数:
- 结束可迭代对象
costs 数组的 n 维索引。
- 返回:
- 回溯n-d 元组列表
一个指向 costs 数组的索引列表,从传递给 find_costs() 的起始位置之一开始,并以给定的 end 索引结束。这些索引指定了从任意给定的起始索引到 end 索引的最小成本路径。(该路径的总成本可以从 find_costs() 返回的 cumulative_costs 数组中读取。)
- class skimage.graph.MCP_Flexible(costs, offsets=None, fully_connected=True)#
基类:
MCP通过 N 维成本数组找到最小成本路径。
请参阅 MCP 的文档以获取完整详情。此类与 MCP 的不同之处在于,可以通过重载(从纯 Python)多个方法来修改算法的行为和/或基于 MCP 创建自定义算法。请注意,goal_reached 也可以在 MCP 类中重载。
- __init__(costs, offsets=None, fully_connected=True, sampling=None)#
查看类文档。
- examine_neighbor(index, new_index, offset_length)#
此方法在每对相邻节点冻结后立即被调用一次。
此方法可以被重载以获取相邻节点的信息,和/或修改MCP算法的行为。一个例子是MCP_Connect类,它使用此钩子检查会合前沿。
- find_costs(starts, ends=None, find_all_ends=True, max_coverage=1.0, max_cumulative_cost=None, max_cost=None)#
从给定的起点找到最小成本路径。
此方法从指定的起始索引之一找到到达指定结束索引的最小成本路径。如果没有给出结束位置,则将找到到达成本数组中每个位置的最小成本路径。
- 参数:
- 开始可迭代对象
一个 n-d 起始索引列表(其中 n 是 costs 数组的维度)。将找到到最近/最便宜起始点的最小成本路径。
- 结束可迭代对象, 可选
一个以 n-d 结尾的索引列表。
- find_all_endsbool, 可选
如果为 ‘True’(默认),将找到到每个指定结束位置的最小成本路径;否则,算法将在找到到任何结束位置的路径时停止。(如果没有指定 ends,则此参数无效。)
- 返回:
- 累计成本ndarray
与 costs 数组形状相同;此数组记录从最近的/最便宜的起始索引到每个考虑的索引的最小成本路径。(如果指定了 ends,则不一定考虑数组中的所有元素:未评估的位置将具有累积成本 inf。如果 find_all_ends 为 ‘False’,则只有指定的结束位置之一将具有有限的累积成本。)
- 回溯ndarray
与 costs 数组形状相同;此数组包含从其前一个索引到任何给定索引的偏移量。偏移索引索引到 offsets 属性,该属性是一个 n-d 偏移量的数组。在 2-d 情况下,如果 offsets[traceback[x, y]] 是 (-1, -1),这意味着在到某个起始位置的最小成本路径中,[x, y] 的前一个索引是 [x+1, y+1]。请注意,如果 offset_index 是 -1,则给定索引未被考虑。
- goal_reached(index, cumcost)#
int goal_reached(int index, float cumcost) 每次从堆中弹出一个索引后,在检查邻居之前,都会调用此方法。
此方法可以被重载以修改MCP算法的行为。例如,可能会在达到某个累积成本时停止算法,或者在前沿距离种子点一定距离时停止算法。
如果算法不应检查当前点的邻居,此方法应返回 1;如果算法已完成,则应返回 2。
- offsets#
!! 由 numpydoc 处理 !!
- traceback(end)#
通过预先计算的回溯数组追踪最小成本路径。
这个便利函数从提供给 find_costs() 的起始索引之一重建到给定结束位置的最小成本路径,该函数必须在之前调用过 find_costs()。在 find_costs() 运行后,可以多次调用此函数。
- 参数:
- 结束可迭代对象
costs 数组的 n 维索引。
- 返回:
- 回溯n-d 元组列表
一个指向 costs 数组的索引列表,从传递给 find_costs() 的起始位置之一开始,并以给定的 end 索引结束。这些索引指定了从任意给定的起始索引到 end 索引的最小成本路径。(该路径的总成本可以从 find_costs() 返回的 cumulative_costs 数组中读取。)
- travel_cost(old_cost, new_cost, offset_length)#
此方法计算从当前节点到下一个节点的旅行成本。默认实现返回 new_cost。重载此方法以适应算法的行为。
- update_node(index, new_index, offset_length)#
当节点更新时调用此方法,在新的索引被推入堆并且回溯映射更新之后。
此方法可以被重载以跟踪算法特定实现所使用的其他数组。例如,MCP_Connect 类使用它来更新一个 id 映射。
- class skimage.graph.MCP_Geometric(costs, offsets=None, fully_connected=True)#
基类:
MCP在 n 维成本数组中找到距离加权的最小成本路径。
请参阅MCP的文档以获取完整详情。此类与MCP的不同之处在于,路径的成本不仅仅是该路径上各成本的总和。
这个类假设成本数组在每个位置包含了通过该位置的单位距离旅行的“成本”。例如,从 (1, 1) 到 (1, 2) 的移动(在 2-d 中)假设起始于像素 (1, 1) 的中心,终止于 (1, 2) 的中心。整个移动的距离为 1,一半通过 (1, 1),一半通过 (1, 2);因此该移动的成本为 (1/2)*costs[1,1] + (1/2)*costs[1,2]。
另一方面,从 (1, 1) 移动到 (2, 2) 是沿着对角线的,长度为 sqrt(2)。这次移动的一半在像素 (1, 1) 内,另一半在 (2, 2) 内,因此这次移动的成本计算为 (sqrt(2)/2)*costs[1,1] + (sqrt(2)/2)*costs[2,2]。
这些计算对于大于1的偏移量来说没有太大意义。使用 sampling 参数来处理各向异性数据。
- __init__(costs, offsets=None, fully_connected=True, sampling=None)#
查看类文档。
- find_costs(starts, ends=None, find_all_ends=True, max_coverage=1.0, max_cumulative_cost=None, max_cost=None)#
从给定的起点找到最小成本路径。
此方法从指定的起始索引之一找到到达指定结束索引的最小成本路径。如果没有给出结束位置,则将找到到达成本数组中每个位置的最小成本路径。
- 参数:
- 开始可迭代对象
一个 n-d 起始索引列表(其中 n 是 costs 数组的维度)。将找到到最近/最便宜起始点的最小成本路径。
- 结束可迭代对象, 可选
一个以 n-d 结尾的索引列表。
- find_all_endsbool, 可选
如果为 ‘True’(默认),将找到到每个指定结束位置的最小成本路径;否则,算法将在找到到任何结束位置的路径时停止。(如果没有指定 ends,则此参数无效。)
- 返回:
- 累计成本ndarray
与 costs 数组形状相同;此数组记录从最近的/最便宜的起始索引到每个考虑的索引的最小成本路径。(如果指定了 ends,则不一定考虑数组中的所有元素:未评估的位置将具有累积成本 inf。如果 find_all_ends 为 ‘False’,则只有指定的结束位置之一将具有有限的累积成本。)
- 回溯ndarray
与 costs 数组形状相同;此数组包含从其前一个索引到任何给定索引的偏移量。偏移索引索引到 offsets 属性,该属性是一个 n-d 偏移量的数组。在 2-d 情况下,如果 offsets[traceback[x, y]] 是 (-1, -1),这意味着在到某个起始位置的最小成本路径中,[x, y] 的前一个索引是 [x+1, y+1]。请注意,如果 offset_index 是 -1,则给定索引未被考虑。
- goal_reached(index, cumcost)#
int goal_reached(int index, float cumcost) 每次从堆中弹出一个索引后,在检查邻居之前,都会调用此方法。
此方法可以被重载以修改MCP算法的行为。例如,可能会在达到某个累积成本时停止算法,或者在前沿距离种子点一定距离时停止算法。
如果算法不应检查当前点的邻居,此方法应返回 1;如果算法已完成,则应返回 2。
- offsets#
!! 由 numpydoc 处理 !!
- traceback(end)#
通过预先计算的回溯数组追踪最小成本路径。
这个便利函数从提供给 find_costs() 的起始索引之一重建到给定结束位置的最小成本路径,该函数必须在之前调用过 find_costs()。在 find_costs() 运行后,可以多次调用此函数。
- 参数:
- 结束可迭代对象
costs 数组的 n 维索引。
- 返回:
- 回溯n-d 元组列表
一个指向 costs 数组的索引列表,从传递给 find_costs() 的起始位置之一开始,并以给定的 end 索引结束。这些索引指定了从任意给定的起始索引到 end 索引的最小成本路径。(该路径的总成本可以从 find_costs() 返回的 cumulative_costs 数组中读取。)
- class skimage.graph.RAG(label_image=None, connectivity=1, data=None, **attr)[源代码][源代码]#
基类:
GraphThe Region Adjacency Graph (RAG) of an image, subclasses
networkx.Graph.- 参数:
- label_imageint 数组
初始分割,每个区域标记为不同的整数。
label_image中的每个唯一值将对应于图中的一个节点。- 连通性 : int in {1, …,
label_image.ndim}, 可选int in {1, …, label_image中像素之间的连通性。对于2D图像,连通性为1对应于上下左右相邻的邻居,而连通性为2还包括对角线相邻的邻居。参见scipy.ndimage.generate_binary_structure()。- datanetworkx.Graph 规范,可选
Initial or additional edges to pass to
networkx.Graphconstructor. Valid edge specifications include edge list (list of tuples), NumPy arrays, and SciPy sparse matrices.- **属性关键字参数, 可选
要添加到图表中的其他属性。
- __init__(label_image=None, connectivity=1, data=None, **attr)[源代码][源代码]#
使用边、名称或图属性初始化一个图。
- 参数:
- incoming_graph_data输入图(可选,默认:无)
用于初始化图的数据。如果为 None(默认),则创建一个空图。数据可以是边列表,或者是任何 NetworkX 图对象。如果相应的可选 Python 包已安装,数据也可以是二维 NumPy 数组、SciPy 稀疏数组或 PyGraphviz 图。
- attr关键字参数,可选(默认=无属性)
要添加到图表中的属性,以键=值对的形式表示。
参见
convert
示例
>>> G = nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc >>> G = nx.Graph(name="my graph") >>> e = [(1, 2), (2, 3), (3, 4)] # list of edges >>> G = nx.Graph(e)
可以分配任意的图属性对(键=值)
>>> G = nx.Graph(e, day="Friday") >>> G.graph {'day': 'Friday'}
- add_edges_from(ebunch_to_add, **attr)[源代码]#
添加 ebunch_to_add 中的所有边。
- 参数:
- ebunch_to_add边缘的容器
容器中的每条边都将被添加到图中。边必须以2元组 (u, v) 或3元组 (u, v, d) 的形式给出,其中 d 是一个包含边数据的字典。
- attr关键字参数, 可选
可以使用关键字参数分配边缘数据(或标签或对象)。
参见
add_edge添加一条边
add_weighted_edges_from添加加权边的便捷方式
注释
添加相同的边两次不会有效果,但每次添加重复边时,任何边数据都会被更新。
在 ebunch 中指定的边属性优先于通过关键字参数指定的属性。
当你从一个正在更改的图的迭代器中添加边时,可能会引发 RuntimeError 并带有消息:RuntimeError: dictionary changed size during iteration。这种情况发生在图的基础字典在迭代过程中被修改时。为了避免这个错误,可以将迭代器评估为一个单独的对象,例如通过使用 list(iterator_of_edges),并将这个对象传递给 G.add_edges_from。
示例
>>> G = nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc >>> G.add_edges_from([(0, 1), (1, 2)]) # using a list of edge tuples >>> e = zip(range(0, 3), range(1, 4)) >>> G.add_edges_from(e) # Add the path graph 0-1-2-3
将数据关联到边
>>> G.add_edges_from([(1, 2), (2, 3)], weight=3) >>> G.add_edges_from([(3, 4), (1, 4)], label="WN2898")
如果使用迭代器修改同一个图,请评估该迭代器。
>>> G = nx.Graph([(1, 2), (2, 3), (3, 4)]) >>> # Grow graph by one new node, adding edges to all existing nodes. >>> # wrong way - will raise RuntimeError >>> # G.add_edges_from(((5, n) for n in G.nodes)) >>> # correct way - note that there will be no self-edge for node 5 >>> G.add_edges_from(list((5, n) for n in G.nodes))
- add_nodes_from(nodes_for_adding, **attr)[源代码]#
添加多个节点。
- 参数:
- nodes_for_adding可迭代容器
一个节点的容器(列表、字典、集合等)。或一个(节点,属性字典)元组的容器。节点属性使用属性字典进行更新。
- attr关键字参数,可选(默认=无属性)
更新节点中的所有节点属性。在节点中以元组形式指定的节点属性优先于通过关键字参数指定的属性。
参见
注释
当从正在更改的图的迭代器中添加节点时,可能会引发 RuntimeError,消息为:RuntimeError: dictionary changed size during iteration。这种情况发生在迭代过程中修改了图的基础字典时。为了避免此错误,请将迭代器评估为单独的对象,例如使用 list(iterator_of_nodes),并将此对象传递给 G.add_nodes_from。
示例
>>> G = nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc >>> G.add_nodes_from("Hello") >>> K3 = nx.Graph([(0, 1), (1, 2), (2, 0)]) >>> G.add_nodes_from(K3) >>> sorted(G.nodes(), key=str) [0, 1, 2, 'H', 'e', 'l', 'o']
使用关键词来更新每个节点的特定节点属性。
>>> G.add_nodes_from([1, 2], size=10) >>> G.add_nodes_from([3, 4], weight=0.4)
使用 (节点, 属性字典) 元组来更新特定节点的属性。
>>> G.add_nodes_from([(1, dict(size=11)), (2, {"color": "blue"})]) >>> G.nodes[1]["size"] 11 >>> H = nx.Graph() >>> H.add_nodes_from(G.nodes(data=True)) >>> H.nodes[1]["size"] 11
如果使用迭代器修改同一个图,请评估该迭代器。
>>> G = nx.Graph([(0, 1), (1, 2), (3, 4)]) >>> # wrong way - will raise RuntimeError >>> # G.add_nodes_from(n + 1 for n in G.nodes) >>> # correct way >>> G.add_nodes_from(list(n + 1 for n in G.nodes))
- add_weighted_edges_from(ebunch_to_add, weight='weight', **attr)[源代码]#
在 ebunch_to_add 中添加带权重的边,并指定权重属性
- 参数:
- ebunch_to_add边缘的容器
列表或容器中的每条边都将被添加到图中。边必须以 3 元组 (u, v, w) 的形式给出,其中 w 是一个数字。
- 重量字符串, 可选 (默认= ‘weight’)
要添加的边权重的属性名称。
- attr关键字参数,可选(默认=无属性)
要为所有边添加/更新的边属性。
参见
add_edge添加一条边
add_edges_from添加多条边
注释
对于 Graph/DiGraph,添加相同的边两次只会更新边数据。对于 MultiGraph/MultiDiGraph,重复的边会被存储。
当从你正在更改的图的迭代器中添加边时,可能会引发 RuntimeError,消息为:RuntimeError: dictionary changed size during iteration。这种情况发生在图的基础字典在迭代过程中被修改时。为了避免这个错误,请将迭代器评估为一个单独的对象,例如通过使用 list(iterator_of_edges),并将此对象传递给 G.add_weighted_edges_from。
示例
>>> G = nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc >>> G.add_weighted_edges_from([(0, 1, 3.0), (1, 2, 7.5)])
在传递之前评估边迭代器
>>> G = nx.Graph([(1, 2), (2, 3), (3, 4)]) >>> weight = 0.1 >>> # Grow graph by one new node, adding edges to all existing nodes. >>> # wrong way - will raise RuntimeError >>> # G.add_weighted_edges_from(((5, n, weight) for n in G.nodes)) >>> # correct way - note that there will be no self-edge for node 5 >>> G.add_weighted_edges_from(list((5, n, weight) for n in G.nodes))
- property adj#
图邻接对象,保存每个节点的邻居。
这个对象是一个只读的类似字典的结构,包含节点键和邻居字典值。邻居字典按邻居键入边数据字典。因此 G.adj[3][2][‘color’] = ‘blue’ 将边 (3, 2) 的颜色设置为 “blue”。
遍历 G.adj 的行为类似于字典。有用的惯用语包括 for nbr, datadict in G.adj[n].items():。
邻居信息也可以通过下标图来提供。因此 for nbr, foovalue in G[node].data(‘foo’, default=1): 是有效的。
对于有向图,G.adj 保存了出边(后继)信息。
- adjacency()[源代码]#
返回一个迭代器,遍历所有节点的 (节点, 邻接字典) 元组。
对于有向图,仅包含出边邻居/邻接关系。
- 返回:
- adj_iter迭代器
图表中所有节点的迭代器,返回 (节点, 邻接字典)。
示例
>>> G = nx.path_graph(4) # or DiGraph, MultiGraph, MultiDiGraph, etc >>> [(n, nbrdict) for n, nbrdict in G.adjacency()] [(0, {1: {}}), (1, {0: {}, 2: {}}), (2, {1: {}, 3: {}}), (3, {2: {}})]
- clear()[源代码]#
从图中移除所有节点和边。
这也会移除名称,以及所有图、节点和边的属性。
示例
>>> G = nx.path_graph(4) # or DiGraph, MultiGraph, MultiDiGraph, etc >>> G.clear() >>> list(G.nodes) [] >>> list(G.edges) []
- clear_edges()[源代码]#
从图中移除所有边,而不改变节点。
示例
>>> G = nx.path_graph(4) # or DiGraph, MultiGraph, MultiDiGraph, etc >>> G.clear_edges() >>> list(G.nodes) [0, 1, 2, 3] >>> list(G.edges) []
- property degree#
图的 DegreeView,如 G.degree 或 G.degree()。
节点的度是与该节点相邻的边的数量。加权节点度是与该节点相邻的边的权值之和。
此对象提供了一个用于 (节点, 度数) 的迭代器,以及用于单个节点的度数查找功能。
- 参数:
- nbunch单个节点、容器或所有节点(默认=所有节点)
视图将仅报告与这些节点相邻的边。
- 重量字符串或None,可选(默认=None)
一个边属性的名称,该属性保存用作权重的数值。如果为 None,则每条边的权重为 1。度是与节点相邻的边权重的总和。
- 返回:
- DegreeView 或 int
如果请求多个节点(默认),返回一个 DegreeView 映射节点到它们的度。如果请求单个节点,返回该节点的度作为一个整数。
示例
>>> G = nx.path_graph(4) # or DiGraph, MultiGraph, MultiDiGraph, etc >>> G.degree[0] # node 0 has degree 1 1 >>> list(G.degree([0, 1, 2])) [(0, 1), (1, 2), (2, 2)]
- edge_subgraph(edges)[源代码]#
返回由指定边诱导的子图。
导出的子图包含 edges 中的每条边以及与这些边中的任何一条相邻的每个节点。
- 参数:
- 边缘可迭代对象
此图中的边的可迭代对象。
- 返回:
- G图
此图的一个边诱导子图,具有相同的边属性。
注释
返回的子图视图中的图、边和节点属性是对原始图中相应属性的引用。该视图是只读的。
要创建一个具有自身边或节点属性副本的子图的全图版本,请使用:
G.edge_subgraph(edges).copy()
示例
>>> G = nx.path_graph(5) >>> H = G.edge_subgraph([(0, 1), (3, 4)]) >>> list(H.nodes) [0, 1, 3, 4] >>> list(H.edges) [(0, 1), (3, 4)]
- property edges#
图的边视图作为 G.edges 或 G.edges()。
edges(self, nbunch=None, data=False, default=None)
EdgeView 提供了对边元组的集合操作以及边属性查找。当调用时,它还提供了一个 EdgeDataView 对象,该对象允许控制对边属性的访问(但不提供集合操作)。因此,G.edges[u, v][‘color’] 提供了边 (u, v) 的颜色属性值,而 for (u, v, c) in G.edges.data(‘color’, default=’red’): 遍历所有边,生成颜色属性,如果颜色属性不存在,则使用默认值 ‘red’。
- 参数:
- nbunch单个节点、容器或所有节点(默认=所有节点)
视图将仅报告这些节点之间的边。
- 数据字符串或布尔值,可选(默认=False)
在3元组 (u, v, ddict[data]) 中返回的边属性。如果为True,则在3元组 (u, v, ddict) 中返回边属性字典。如果为False,则返回2元组 (u, v)。
- 默认值,可选(默认=无)
用于没有请求属性的边的值。仅在数据不是 True 或 False 时相关。
- 返回:
- 边缘EdgeView
边缘属性的视图,通常它迭代遍历 (u, v) 或 (u, v, d) 形式的边缘元组,但也可以用于属性查找,如 edges[u, v][‘foo’]。
注释
不在图中的 nbunch 节点将被(安静地)忽略。对于有向图,这将返回出边。
示例
>>> G = nx.path_graph(3) # or MultiGraph, etc >>> G.add_edge(2, 3, weight=5) >>> [e for e in G.edges] [(0, 1), (1, 2), (2, 3)] >>> G.edges.data() # default data is {} (empty dict) EdgeDataView([(0, 1, {}), (1, 2, {}), (2, 3, {'weight': 5})]) >>> G.edges.data("weight", default=1) EdgeDataView([(0, 1, 1), (1, 2, 1), (2, 3, 5)]) >>> G.edges([0, 3]) # only edges from these nodes EdgeDataView([(0, 1), (3, 2)]) >>> G.edges(0) # only edges from node 0 EdgeDataView([(0, 1)])
- fresh_copy()[源代码][源代码]#
返回一个具有相同数据结构的新副本图。
一个全新的副本没有节点、边或图属性。它与当前图的数据结构相同。此方法通常用于创建图的空版本。
当使用networkx v2子类化Graph时,这是必需的,并且不会对v1造成问题。以下是从1.x迁移到2.x文档中的更多细节:
With the new GraphViews (SubGraph, ReversedGraph, etc) you can't assume that ``G.__class__()`` will create a new instance of the same graph type as ``G``. In fact, the call signature for ``__class__`` differs depending on whether ``G`` is a view or a base class. For v2.x you should use ``G.fresh_copy()`` to create a null graph of the correct type---ready to fill with nodes and edges.
- get_edge_data(u, v, default=None)[源代码]#
返回与边 (u, v) 关联的属性字典。
这与 G[u][v] 相同,但如果边不存在,则返回默认值而不是异常。
- 参数:
- u, v节点
- 默认值: 任何 Python 对象 (默认=None)
如果未找到边 (u, v),则返回的值。
- 返回:
- edge_dict字典
边缘属性字典。
示例
>>> G = nx.path_graph(4) # or DiGraph, MultiGraph, MultiDiGraph, etc >>> G[0][1] {}
警告:不允许对 G[u][v] 进行赋值。但可以安全地对属性 G[u][v][‘foo’] 进行赋值。
>>> G[0][1]["weight"] = 7 >>> G[0][1]["weight"] 7 >>> G[1][0]["weight"] 7
>>> G = nx.path_graph(4) # or DiGraph, MultiGraph, MultiDiGraph, etc >>> G.get_edge_data(0, 1) # default edge data is {} {} >>> e = (0, 1) >>> G.get_edge_data(*e) # tuple form {} >>> G.get_edge_data("a", "b", default=0) # edge not in graph, return 0 0
- has_edge(u, v)[源代码]#
如果边 (u, v) 在图中,则返回 True。
这与 v in G[u] 相同,但不会引发 KeyError 异常。
- 参数:
- u, v节点
节点可以是,例如,字符串或数字。节点必须是可哈希的(且不为 None)Python 对象。
- 返回:
- edge_ind布尔
如果边在图中则为 True,否则为 False。
示例
>>> G = nx.path_graph(4) # or DiGraph, MultiGraph, MultiDiGraph, etc >>> G.has_edge(0, 1) # using two nodes True >>> e = (0, 1) >>> G.has_edge(*e) # e is a 2-tuple (u, v) True >>> e = (0, 1, {"weight": 7}) >>> G.has_edge(*e[:2]) # e is a 3-tuple (u, v, data_dictionary) True
以下语法是等价的:
>>> G.has_edge(0, 1) True >>> 1 in G[0] # though this gives KeyError if 0 not in G True
- has_node(n)[源代码]#
如果图中包含节点 n,则返回 True。
与 n in G 相同
- 参数:
- n节点
示例
>>> G = nx.path_graph(3) # or DiGraph, MultiGraph, MultiDiGraph, etc >>> G.has_node(0) True
它更易读且使用更简单。
>>> 0 in G True
- merge_nodes(src, dst, weight_func=<function min_weight>, in_place=True, extra_arguments=None, extra_keywords=None)[源代码][源代码]#
合并节点 src 和 dst。
新的组合节点与 src 和 dst 的所有邻居相邻。weight_func 被调用来决定新节点上边的权重。
- 参数:
- src, dst整数
待合并的节点。
- weight_func可调用,可选
Function to decide the attributes of edges incident on the new node. For each neighbor n for src and dst, weight_func will be called as follows: weight_func(src, dst, n, *extra_arguments, **extra_keywords). src, dst and n are IDs of vertices in the RAG object which is in turn a subclass of
networkx.Graph. It is expected to return a dict of attributes of the resulting edge.- in_placebool, 可选
如果设置为 True,合并后的节点将具有 dst 的 id,否则合并后的节点将有一个新的 id,该 id 会被返回。
- extra_arguments序列,可选
传递给 weight_func 的额外位置参数序列。
- extra_keywords字典,可选
传递给 weight_func 的关键字参数的字典。
- 返回:
- id整数
新节点的id。
注释
如果 in_place 是 False ,生成的节点将有一个新的id,而不是 dst。
- property name#
图形的字符串标识符。
此图属性出现在属性字典 G.graph 中,以字符串 “name” 为键。同时也是一个属性(技术上是一个属性)`G.name`。这完全由用户控制。
- nbunch_iter(nbunch=None)[源代码]#
返回一个迭代器,遍历包含在 nbunch 中且也在图中的节点。
nbunch 中的节点会被检查是否属于图,如果不属于,则会被静默忽略。
- 参数:
- nbunch单个节点、容器或所有节点(默认=所有节点)
视图将仅报告与这些节点相邻的边。
- 返回:
- niter迭代器
遍历nbunch中也在图中的节点。如果nbunch为None,则遍历图中所有节点。
- Raises:
- NetworkX错误
如果 nbunch 不是一个节点或节点序列。如果 nbunch 中的一个节点不可哈希。
参见
Graph.__iter__
注释
当 nbunch 是一个迭代器时,返回的迭代器直接从 nbunch 中产生值,当 nbunch 耗尽时,返回的迭代器也会耗尽。
要测试 nbunch 是否为一个单一节点,可以使用 “if nbunch in self:”,即使在通过此例程处理后。
如果 nbunch 不是一个节点或一个(可能为空的)序列/迭代器或 None,则会引发
NetworkXError。此外,如果 nbunch 中的任何对象不可哈希,也会引发NetworkXError。
- neighbors(n)[源代码]#
返回一个遍历节点 n 所有邻居的迭代器。
这与 iter(G[n]) 相同
- 参数:
- n节点
图中的一个节点
- 返回:
- 邻居迭代器
遍历节点 n 的所有邻居的迭代器
- Raises:
- NetworkX错误
如果节点 n 不在图中。
注释
访问邻居的替代方法有
G.adj[n]或G[n]:>>> G = nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc >>> G.add_edge("a", "b", weight=7) >>> G["a"] AtlasView({'b': {'weight': 7}}) >>> G = nx.path_graph(4) >>> [n for n in G[0]] [1]
示例
>>> G = nx.path_graph(4) # or DiGraph, MultiGraph, MultiDiGraph, etc >>> [n for n in G.neighbors(0)] [1]
- property nodes#
图的节点视图,如 G.nodes 或 G.nodes()。
可以作为 G.nodes 用于数据查找和集合操作。也可以作为 G.nodes(data=’color’, default=None) 来返回一个 NodeDataView,它报告特定的节点数据但不执行集合操作。它还呈现了一个类似字典的接口,其中 G.nodes.items() 迭代遍历 (node, nodedata) 2元组,而 G.nodes[3][‘foo’] 提供节点 3 的 foo 属性的值。此外,视图 G.nodes.data(‘foo’) 提供了一个类似字典的接口,用于访问每个节点的 foo 属性。G.nodes.data(‘foo’, default=1) 为没有 foo 属性的节点提供默认值。
- 参数:
- 数据字符串或布尔值,可选(默认=False)
返回的节点属性为 2-元组 (n, ddict[data])。如果为 True,返回整个节点属性字典作为 (n, ddict)。如果为 False,仅返回节点 n。
- 默认值,可选(默认=无)
用于没有请求属性的节点的值。仅在数据不是 True 或 False 时相关。
- 返回:
- NodeView
允许对节点进行集合操作,以及节点属性字典查找和调用以获取 NodeDataView。NodeDataView 迭代 (n, data) 并且没有集合操作。NodeView 迭代 n 并包含集合操作。
当调用时,如果数据为 False,则返回节点上的迭代器。否则返回 2-元组 (节点, 属性值) 的迭代器,其中属性在 data 中指定。如果数据为 True,则属性变为整个数据字典。
注释
如果你的节点数据不需要,使用表达式
for n in G或list(G)会更简单且等效。示例
有两种简单的方法可以获取图中的所有节点列表:
>>> G = nx.path_graph(3) >>> list(G.nodes) [0, 1, 2] >>> list(G) [0, 1, 2]
要获取节点数据以及节点:
>>> G.add_node(1, time="5pm") >>> G.nodes[0]["foo"] = "bar" >>> list(G.nodes(data=True)) [(0, {'foo': 'bar'}), (1, {'time': '5pm'}), (2, {})] >>> list(G.nodes.data()) [(0, {'foo': 'bar'}), (1, {'time': '5pm'}), (2, {})]
>>> list(G.nodes(data="foo")) [(0, 'bar'), (1, None), (2, None)] >>> list(G.nodes.data("foo")) [(0, 'bar'), (1, None), (2, None)]
>>> list(G.nodes(data="time")) [(0, None), (1, '5pm'), (2, None)] >>> list(G.nodes.data("time")) [(0, None), (1, '5pm'), (2, None)]
>>> list(G.nodes(data="time", default="Not Available")) [(0, 'Not Available'), (1, '5pm'), (2, 'Not Available')] >>> list(G.nodes.data("time", default="Not Available")) [(0, 'Not Available'), (1, '5pm'), (2, 'Not Available')]
如果你的某些节点具有属性,而其余节点被假定为具有默认属性值,你可以使用 default 关键字参数创建一个节点/属性对的字典,以确保该值永远不会为 None:
>>> G = nx.Graph() >>> G.add_node(0) >>> G.add_node(1, weight=2) >>> G.add_node(2, weight=3) >>> dict(G.nodes(data="weight", default=1)) {0: 1, 1: 2, 2: 3}
- number_of_edges(u=None, v=None)[源代码]#
返回两个节点之间的边数。
- 参数:
- u, v节点,可选(默认=所有边)
如果指定了 u 和 v,则返回 u 和 v 之间的边数。否则返回所有边的总数。
- 返回:
- nedges整数
图中的边数。如果指定了节点 u 和 v,则返回这两个节点之间的边数。如果图是有向的,则仅返回从 u 到 v 的边数。
参见
示例
对于无向图,此方法计算图中的边总数:
>>> G = nx.path_graph(4) >>> G.number_of_edges() 3
如果你指定两个节点,这将计算连接这两个节点的边的总数:
>>> G.number_of_edges(0, 1) 1
对于有向图,此方法可以计算从 u 到 v 的有向边的总数:
>>> G = nx.DiGraph() >>> G.add_edge(0, 1) >>> G.add_edge(1, 0) >>> G.number_of_edges(0, 1) 1
- number_of_nodes()[源代码]#
返回图中的节点数量。
- 返回:
- nnodes整数
图中的节点数量。
参见
order相同的方法
__len__相同的方法
示例
>>> G = nx.path_graph(3) # or DiGraph, MultiGraph, MultiDiGraph, etc >>> G.number_of_nodes() 3
- order()[源代码]#
返回图中的节点数量。
- 返回:
- nnodes整数
图中的节点数量。
参见
number_of_nodes相同的方法
__len__相同的方法
示例
>>> G = nx.path_graph(3) # or DiGraph, MultiGraph, MultiDiGraph, etc >>> G.order() 3
- remove_edge(u, v)[源代码]#
移除 u 和 v 之间的边。
- 参数:
- u, v节点
移除节点 u 和 v 之间的边。
- Raises:
- NetworkX错误
如果 u 和 v 之间没有边。
参见
remove_edges_from移除一组边
示例
>>> G = nx.path_graph(4) # or DiGraph, etc >>> G.remove_edge(0, 1) >>> e = (1, 2) >>> G.remove_edge(*e) # unpacks e from an edge tuple >>> e = (2, 3, {"weight": 7}) # an edge with attribute data >>> G.remove_edge(*e[:2]) # select first part of edge tuple
- remove_edges_from(ebunch)[源代码]#
移除 ebunch 中指定的所有边。
- 参数:
- ebunch: 边元组的列表或容器
列表或容器中的每条边都将从图中移除。这些边可以是:
2-元组 (u, v) 表示 u 和 v 之间的边。
3元组 (u, v, k) 其中 k 被忽略。
参见
remove_edge删除单条边
注释
如果 ebunch 中的边不在图中,将静默失败。
示例
>>> G = nx.path_graph(4) # or DiGraph, MultiGraph, MultiDiGraph, etc >>> ebunch = [(1, 2), (2, 3)] >>> G.remove_edges_from(ebunch)
- remove_node(n)[源代码]#
移除节点 n。
移除节点 n 及其所有相邻边。尝试移除不存在的节点将引发异常。
- 参数:
- n节点
图中的一个节点
- Raises:
- NetworkX错误
如果 n 不在图中。
示例
>>> G = nx.path_graph(3) # or DiGraph, MultiGraph, MultiDiGraph, etc >>> list(G.edges) [(0, 1), (1, 2)] >>> G.remove_node(1) >>> list(G.edges) []
- remove_nodes_from(nodes)[源代码]#
移除多个节点。
- 参数:
- 节点可迭代容器
节点容器(列表、字典、集合等)。如果容器中的节点不在图中,则会被静默忽略。
参见
注释
当从正在更改的图的迭代器中移除节点时,会引发 RuntimeError 并带有消息:RuntimeError: dictionary changed size during iteration。这种情况发生在图的基础字典在迭代期间被修改时。为了避免这个错误,可以将迭代器评估为一个单独的对象,例如通过使用 list(iterator_of_nodes),并将此对象传递给 G.remove_nodes_from。
示例
>>> G = nx.path_graph(3) # or DiGraph, MultiGraph, MultiDiGraph, etc >>> e = list(G.nodes) >>> e [0, 1, 2] >>> G.remove_nodes_from(e) >>> list(G.nodes) []
如果使用迭代器修改同一个图,请评估该迭代器。
>>> G = nx.Graph([(0, 1), (1, 2), (3, 4)]) >>> # this command will fail, as the graph's dict is modified during iteration >>> # G.remove_nodes_from(n for n in G.nodes if n < 2) >>> # this command will work, since the dictionary underlying graph is not modified >>> G.remove_nodes_from(list(n for n in G.nodes if n < 2))
- size(weight=None)[源代码]#
返回边的数量或所有边权重的总和。
- 参数:
- 重量字符串或None,可选(默认=None)
保存用作权重的数值的边属性。如果为 None,则每条边的权重为 1。
- 返回:
- 大小数字
边的数量或(如果提供了权重关键字)总权重和。
如果 weight 是 None,返回一个 int。否则返回一个 float(或者更一般的数字类型,如果权重是更一般的类型)。
示例
>>> G = nx.path_graph(4) # or DiGraph, MultiGraph, MultiDiGraph, etc >>> G.size() 3
>>> G = nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc >>> G.add_edge("a", "b", weight=2) >>> G.add_edge("b", "c", weight=4) >>> G.size() 2 >>> G.size(weight="weight") 6.0
- subgraph(nodes)[源代码]#
返回在 nodes 上诱导的子图的子图视图。
图的诱导子图包含 nodes 中的节点以及这些节点之间的边。
- 参数:
- 节点列表, 可迭代对象
一个节点容器,将遍历一次。
- 返回:
- G子图视图
图的子图视图。图结构不能更改,但节点/边属性可以更改,并且与原始图共享。
注释
图、边和节点的属性与原始图共享。视图排除了对图结构的更改,但对属性的更改会反映在原始图中。
要创建一个具有自己的边/节点属性副本的子图,请使用:G.subgraph(nodes).copy()
对于将图就地缩减为子图,您可以移除节点:G.remove_nodes_from([n for n in G if n not in set(nodes)])
子图视图有时并不是你想要的。在大多数情况下,如果你想做的事情不仅仅是简单地查看诱导边,那么通过代码创建一个独立的子图会更有意义,例如:
# Create a subgraph SG based on a (possibly multigraph) G SG = G.__class__() SG.add_nodes_from((n, G.nodes[n]) for n in largest_wcc) if SG.is_multigraph(): SG.add_edges_from( (n, nbr, key, d) for n, nbrs in G.adj.items() if n in largest_wcc for nbr, keydict in nbrs.items() if nbr in largest_wcc for key, d in keydict.items() ) else: SG.add_edges_from( (n, nbr, d) for n, nbrs in G.adj.items() if n in largest_wcc for nbr, d in nbrs.items() if nbr in largest_wcc ) SG.graph.update(G.graph)
示例
>>> G = nx.path_graph(4) # or DiGraph, MultiGraph, MultiDiGraph, etc >>> H = G.subgraph([0, 1, 2]) >>> list(H.edges) [(0, 1), (1, 2)]
- to_directed(as_view=False)[源代码]#
返回图的有向表示。
- 返回:
- GDiGraph
一个具有相同名称、相同节点,并且每条边 (u, v, data) 被替换为两条有向边 (u, v, data) 和 (v, u, data) 的有向图。
注释
这将返回边的“深拷贝”、节点的和图的属性,尝试完全复制所有数据和引用。
这与类似的 D=DiGraph(G) 形成对比,后者返回数据的浅拷贝。
有关浅拷贝和深拷贝的更多信息,请参阅Python的copy模块,https://docs.python.org/3/library/copy.html。
警告:如果你已经子类化了 Graph 以在数据结构中使用类似字典的对象,这些更改不会转移到此方法创建的 DiGraph 中。
示例
>>> G = nx.Graph() # or MultiGraph, etc >>> G.add_edge(0, 1) >>> H = G.to_directed() >>> list(H.edges) [(0, 1), (1, 0)]
如果已经指向,返回一个(深度)副本
>>> G = nx.DiGraph() # or MultiDiGraph, etc >>> G.add_edge(0, 1) >>> H = G.to_directed() >>> list(H.edges) [(0, 1)]
- to_undirected(as_view=False)[源代码]#
返回图的无向副本。
- 参数:
- as_viewbool (可选, 默认=False)
如果为真,返回原始无向图的视图。
- 返回:
- G图/多重图
图的深拷贝。
参见
Graph,copy,add_edge,add_edges_from
注释
这将返回边的“深拷贝”、节点的和图的属性,尝试完全复制所有数据和引用。
这与类似的 G = nx.DiGraph(D) 形成对比,后者返回数据的浅拷贝。
有关浅拷贝和深拷贝的更多信息,请参阅Python的copy模块,https://docs.python.org/3/library/copy.html。
警告:如果你已经子类化了 DiGraph 以在数据结构中使用类似字典的对象,这些更改不会转移到此方法创建的 Graph 中。
示例
>>> G = nx.path_graph(2) # or MultiGraph, etc >>> H = G.to_directed() >>> list(H.edges) [(0, 1), (1, 0)] >>> G2 = H.to_undirected() >>> list(G2.edges) [(0, 1)]
- update(edges=None, nodes=None)[源代码]#
使用节点/边/图作为输入来更新图。
类似于 dict.update,此方法接受一个图作为输入,将该图的节点和边添加到此图中。它也可以接受两个输入:边和节点。最后,它可以只接受边或节点。要仅指定节点,必须使用关键字 nodes。
边和节点的集合的处理方式类似于 add_edges_from/add_nodes_from 方法。当迭代时,它们应产生 2 元组 (u, v) 或 3 元组 (u, v, datadict)。
- 参数:
- 边缘图对象,边集合,或无
第一个参数可以是一个图或一些边。如果它具有 nodes 和 edges 属性,则它被视为类似图的对象,并且这些属性被用作要添加到图中的节点和边的集合。如果第一个参数没有这些属性,则将其视为边的集合并添加到图中。如果第一个参数为 None,则不添加任何边。
- 节点节点集合,或 None
第二个参数被视为要添加到图中的节点集合,除非它是 None。如果 edges is None 且 nodes is None,则会引发异常。如果第一个参数是 Graph,则 nodes 将被忽略。
参见
add_edges_from向图添加多条边
add_nodes_from向图中添加多个节点
注释
如果你想使用邻接结构来更新图,从邻接关系中获取边/节点是很直接的。以下示例提供了常见情况,你的邻接关系可能略有不同,需要对这些示例进行调整:
>>> # dict-of-set/list/tuple >>> adj = {1: {2, 3}, 2: {1, 3}, 3: {1, 2}} >>> e = [(u, v) for u, nbrs in adj.items() for v in nbrs] >>> G.update(edges=e, nodes=adj)
>>> DG = nx.DiGraph() >>> # dict-of-dict-of-attribute >>> adj = {1: {2: 1.3, 3: 0.7}, 2: {1: 1.4}, 3: {1: 0.7}} >>> e = [(u, v, {"weight": d}) for u, nbrs in adj.items() for v, d in nbrs.items()] >>> DG.update(edges=e, nodes=adj)
>>> # dict-of-dict-of-dict >>> adj = {1: {2: {"weight": 1.3}, 3: {"color": 0.7, "weight": 1.2}}} >>> e = [(u, v, {"weight": d}) for u, nbrs in adj.items() for v, d in nbrs.items()] >>> DG.update(edges=e, nodes=adj)
>>> # predecessor adjacency (dict-of-set) >>> pred = {1: {2, 3}, 2: {3}, 3: {3}} >>> e = [(v, u) for u, nbrs in pred.items() for v in nbrs]
>>> # MultiGraph dict-of-dict-of-dict-of-attribute >>> MDG = nx.MultiDiGraph() >>> adj = { ... 1: {2: {0: {"weight": 1.3}, 1: {"weight": 1.2}}}, ... 3: {2: {0: {"weight": 0.7}}}, ... } >>> e = [ ... (u, v, ekey, d) ... for u, nbrs in adj.items() ... for v, keydict in nbrs.items() ... for ekey, d in keydict.items() ... ] >>> MDG.update(edges=e)
示例
>>> G = nx.path_graph(5) >>> G.update(nx.complete_graph(range(4, 10))) >>> from itertools import combinations >>> edges = ( ... (u, v, {"power": u * v}) ... for u, v in combinations(range(10, 20), 2) ... if u * v < 225 ... ) >>> nodes = [1000] # for singleton, use a container >>> G.update(edges, nodes)